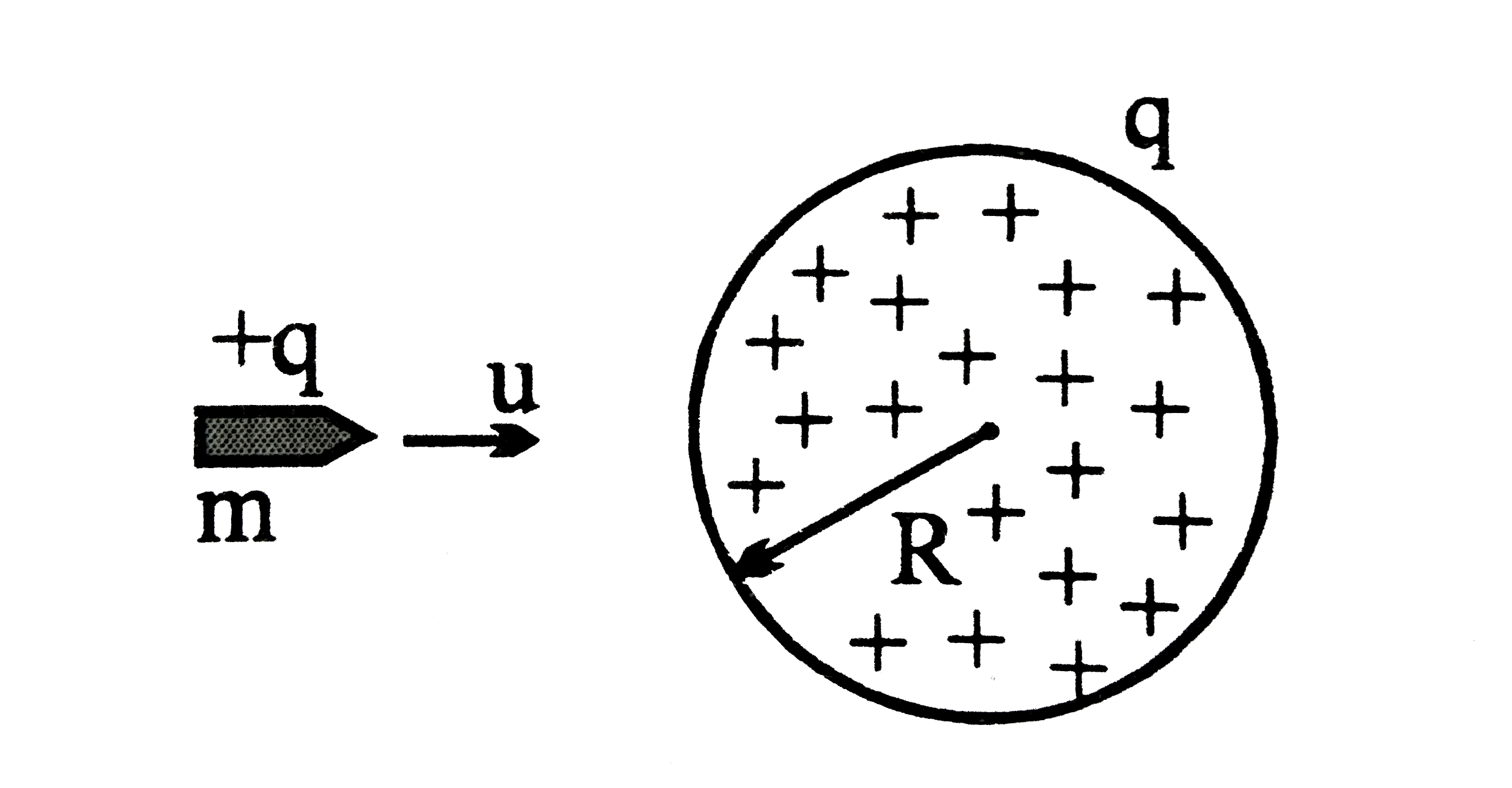
A bullet of mass m and charge $q$ is fired towards a solid unifromly charged sphere of redius $R$ and total cbharge $+ q$ . If it strikes the surface of sphere with speed $u$ , find the minimum speeed $u$ so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrositatic forces )
.

A

$\frac{q}{\sqrt{2 π ɛ_{0} m R}}$

B

$\frac{q}{\sqrt{4 π ɛ_{0} m R}}$

C

$\frac{q}{\sqrt{8 π ɛ_{0} m R}}$

D

$(s q) r t 3 \frac{q}{\sqrt{4 π ɛ_{0} m R}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$v_{s}$ = Potential at surfce $= \frac{1}{4 π \in_{0}} \frac{q}{R}$
$V_{in} = \frac{K Q (3 R^{2} - r^{2})}{2 R^{3}}$
$V_{0} = \frac{3}{2} \frac{1}{4 π \in_{0}} \frac{q}{R}$
To pentrate it must reach cenyre of sphere.
From energy conservation
$\frac{1}{2} μ^{2}_\frac{1}{4 π \in_{0}} \frac{q . q}{R} = 0 + \frac{3}{2} . \frac{1}{4 π \in_{0}}, \frac{q q}{R}$
$\frac{1}{2} μ^{2} = \frac{1}{2} \frac{1}{4 π \in_{0}} \frac{q^{2}}{R}, E = \frac{m g}{2 q}$
$u^{2} = \frac{q^{2}}{4 π \in_{0} m R}$
$u = \frac{q}{\sqrt{4 π \in_{0} m R}}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
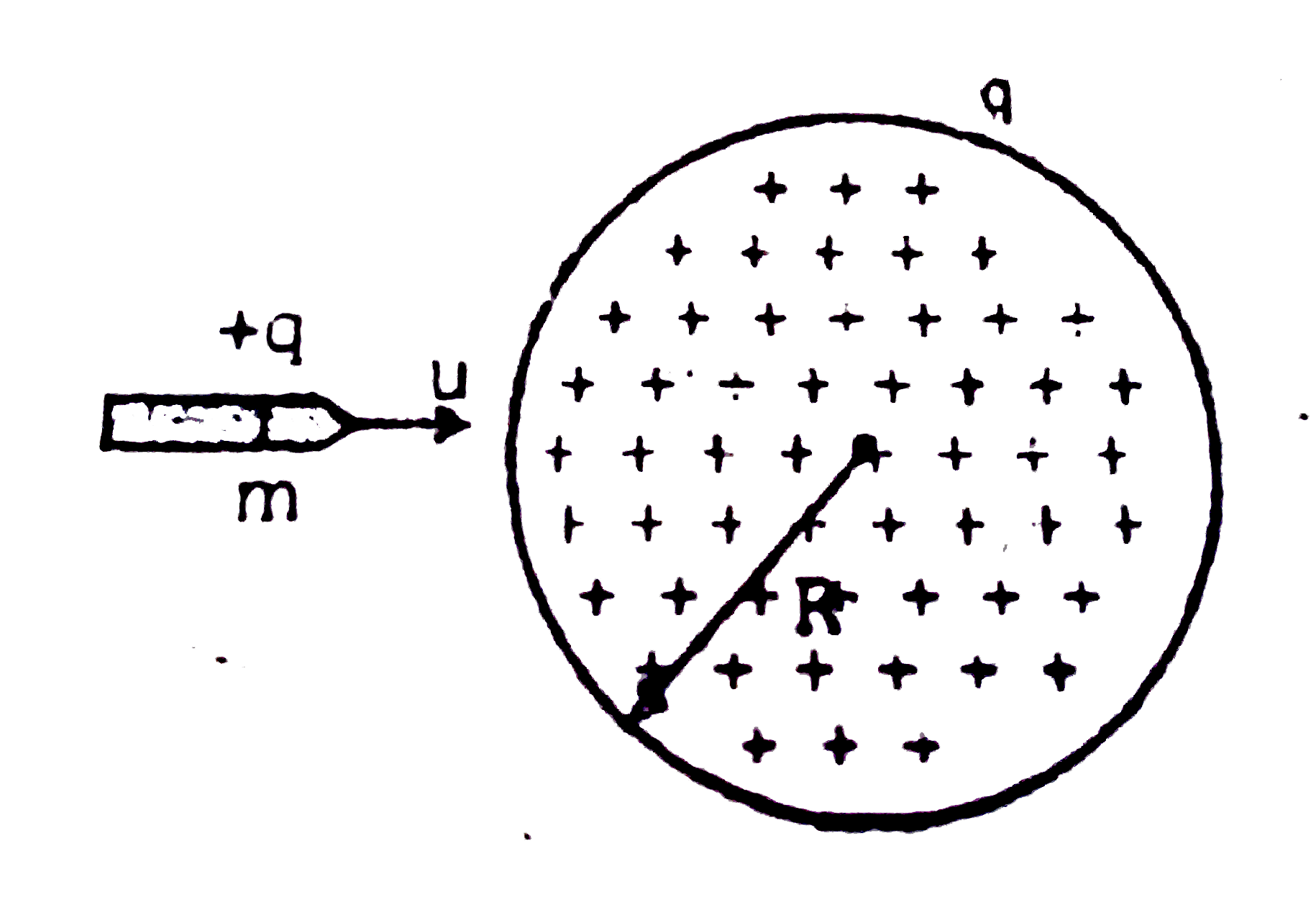
A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)

A $\frac{q}{\sqrt{2 π ε_{0} m R}}$
B $\frac{q}{\sqrt{4 π ε_{0} m R}}$
C $\frac{q}{\sqrt{8 π ε_{0} m R}}$
D $\frac{\sqrt{3} q}{\sqrt{4 π ε_{0} m R}}$
Question 2 - Select One
A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
A $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R}}$
B $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R^{2}}}$
C $\sqrt{\frac{1}{4 π ε_{0}} \frac{q Q}{m R^{3}}}$
D $\sqrt{\frac{1}{4 π ε_{0}} \frac{m}{q Q}}$
Question 3 - Select One
Consider a solid sphere of radius r and mass m which has a charge q distributed uniformly over its volume. The sphere is rotated about a diameter with an angular speed $ω$ . The magnetic moment of the sphere is
A $\frac{1}{3} q ω r^{2}$
B $\frac{1}{5} q ω r^{2}$
C $\frac{1}{7} q ω r^{2}$
D $\frac{1}{9} q ω r^{2}$

Recommended Questions

Home
Ask Doubt
Profile