A unifrom surcace charfge of denstity σ is given to quarter infinite non conducting place in fist quardrant of x−y plane . Find the z-compounct of the elctric field at the point (0, 0, x) Hence or otherwise find the potential difference between the points (0, 0, d) and (0, 0, 2d)
 .
.
The correct Answer is:σ8ɛ0,σd8ɛ_0
(a) Field due to infinite surface at (0, 0, z)
→E=σ2∈0ˆk
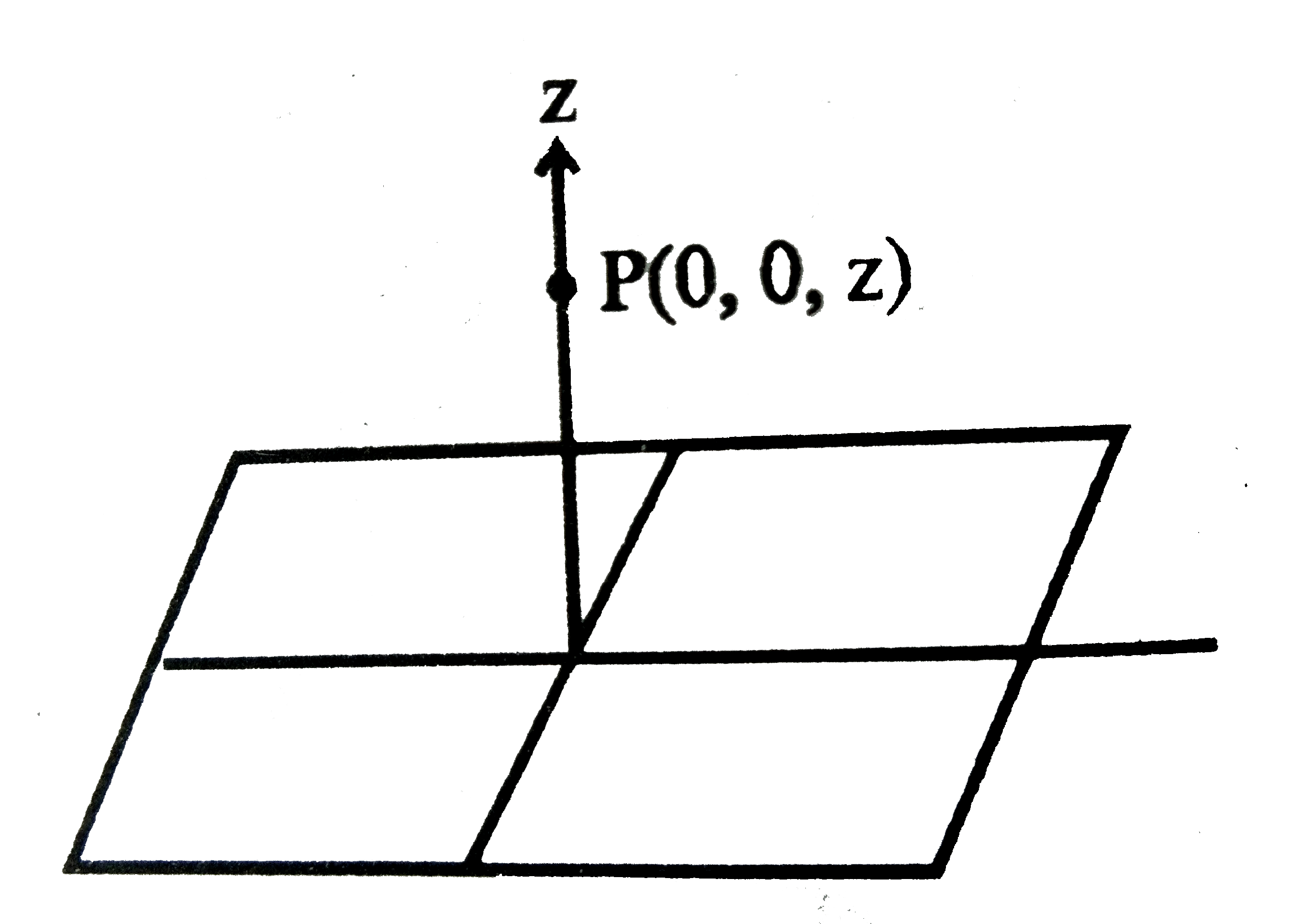
so z compnent of field due to quarter part
→E=14(σ2∈0)ˆk
(b) ∫vvdV=−∫1ddEzdz
ΔV=−−∫2ddσ8∈0dx⇒ΔV=−σ8∈0(Z)2dd
ΔV=−σd8∈0dz⇒ΔaV=−σ8∈0(z)pd2d
ΔV=−σd8∈0.
Similar Questions
A uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).
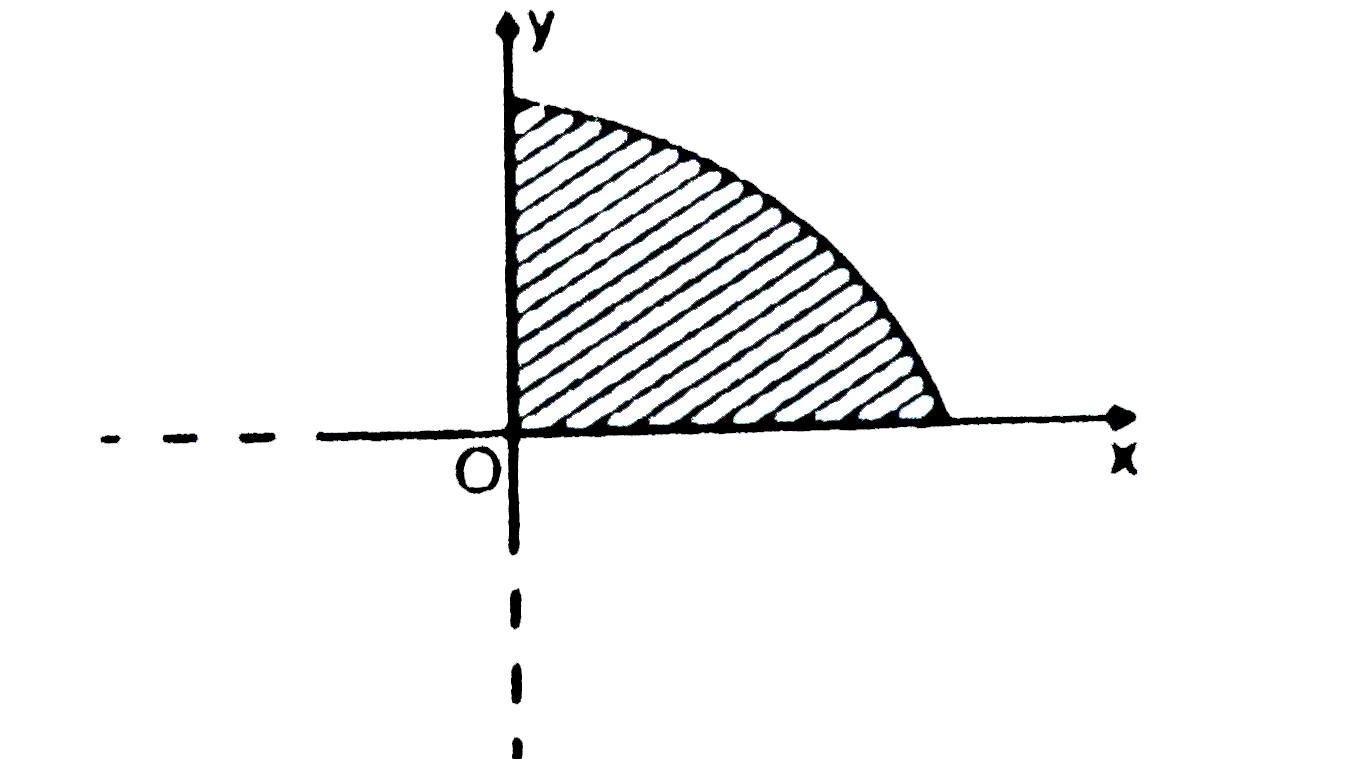
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
View SolutionElectric field in a region is given by E=(2ˆi+3ˆj−4ˆk)V/m. Find the potential difference between points (0, 0, 0) and (1,2,3) in this region.
View SolutionA uniform electric field exists in x y plane as shown in Fig. 3.45. Find the potential difference. Between origin O and A(d,d,0).
 .
.
View SolutionFind the acute angle between the lines x=y: z=0 and x=0z=0
View SolutionFind the shortest distance between the planes: x+y−z+4=0and2x−2y−2z+10=0
View SolutionFind the relation between x and y, if the points (0,0), (1,2) and (x,y) are collinear.
View SolutionFind the acute angle between the lines 2x−y+3=0 and x+y+2=0.
View SolutionFind the foot of perpendicular drawn from the point P(0, 0, 0) to the plane x+2y+2z=13.
View SolutionFind the distance between the planes x+2y+3z+7=0 and 2x+4y+6z+7=0.
View Solution
