A uniform magnetic field →B fills a cylindrical volumes of radius R. A metal rod CD of length l is placed inside the cylinder along a chord of the circular cross-section as shown in the figure. If the magnitude of magnetic field increases in the direction of field at a constant rate dB/dt, find the magnetitude and direction of the EMF induced in the rod.

The correct Answer is:l2dBdt√R2−l24
E,=Eelectrostatic
E=Einduce
∮→E.→dl=ddt→B.→A
E2πr=dBdt.πr2
E=r2dBdt

VD−VA=−∫→E.d→x=−∫E'dxcos(π−0)
=∫Edxcosθ
VD−VA=12∫rdBdtdxcosθ=12dBdt∫bdx
=12dBdt.b∫L/20dx=12dBdt√R2−L24×L2
VD−VC=L2√R2−L24dBdt
V∈duced=AdBdt=2×12×L2×√R2−L24dBdt
V∈duce=L2√R2−L24dBdt
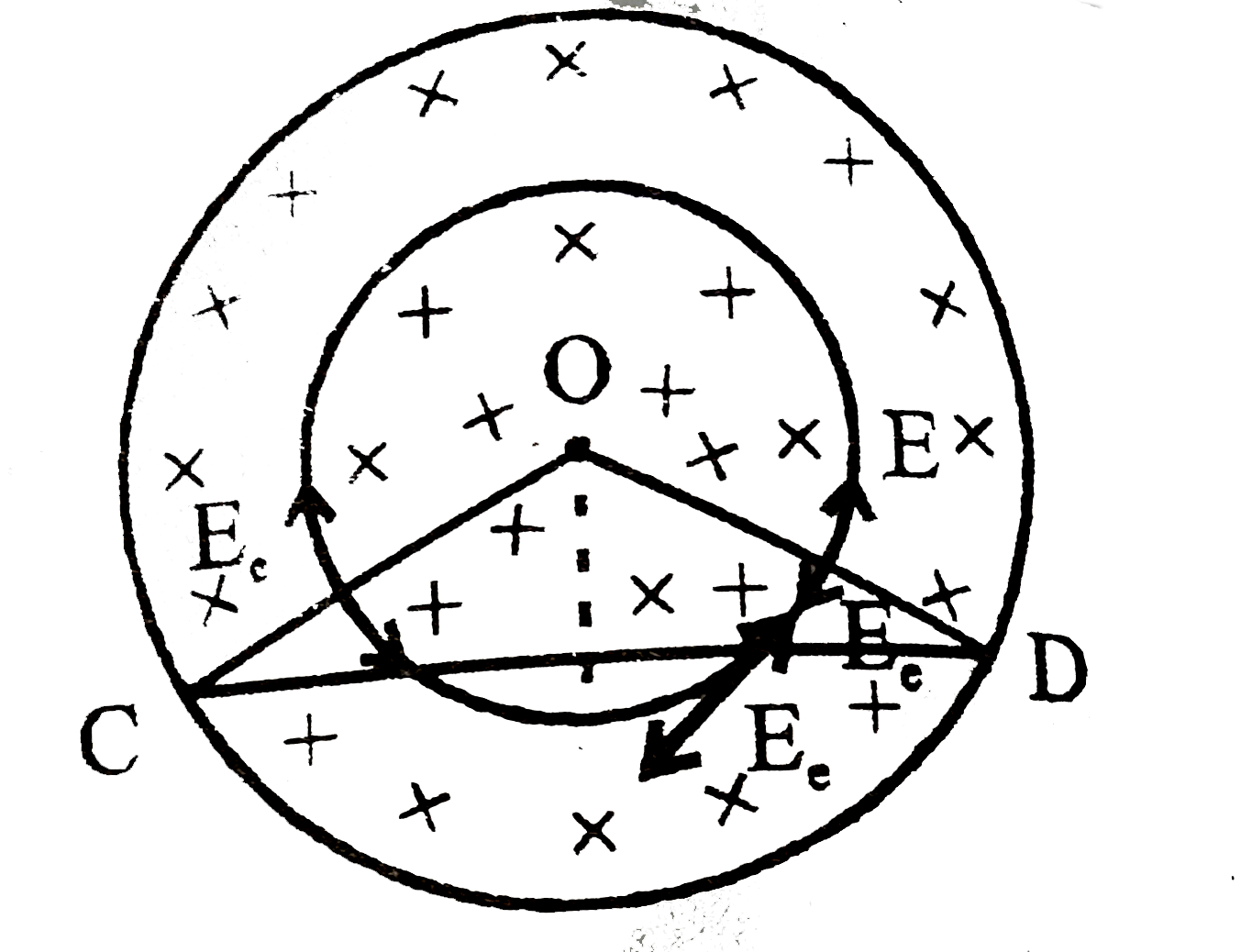
VCO+VDC+VOC=12√R2−L24dBdt
VCO and VOC are 0, because E and dl are ⊥
VCD=L2√R2−L2/4dBdt
Similar Questions
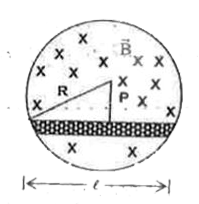
A uniform magneitc field B fills a cylindrical volume of radius R, A metal rod of length l is placed as shown. If B is changing at the rate of dB/dt, the emf that is produced by the changing magnetic field is ξ here p = √R2−(l2)2. then
View Solutiona uniform magnetic field of induction B fills a cylindrical volume of radius R. A rod AB of length 2l is placed as shown in . If B changing at the rate dB/dt, the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
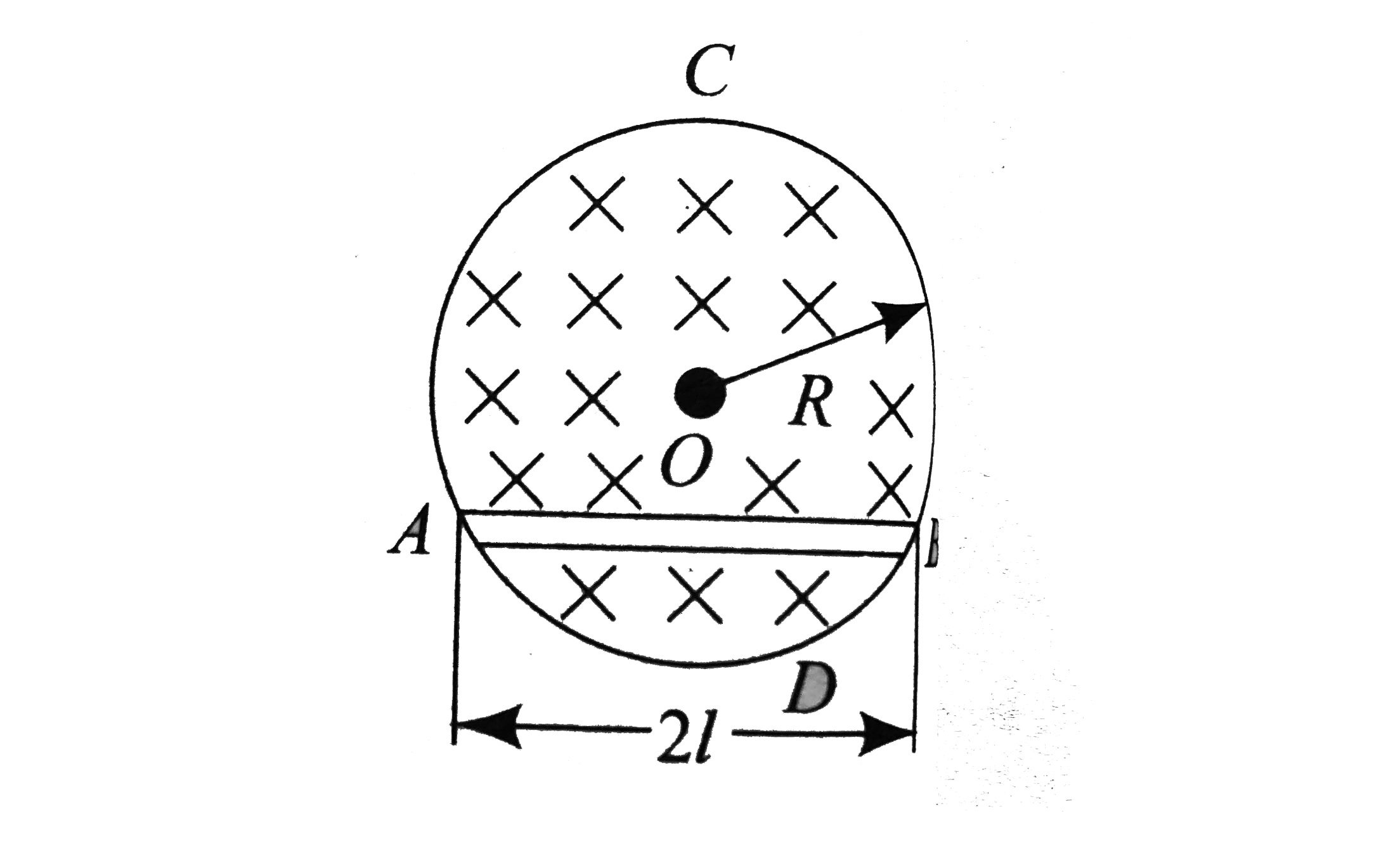
View Solution
Knowledge Check
A uniform magneitc field B fills a cylindrical volume of radius R, A metal rod of length l is placed as shown. If B is changing at the rate of dB/dt, the emf that is produced by the changing magnetic field is ξ here p = √R2−(l2)2. then
 AThe magnitude of the electric field created is 12rdBdtBThe magnitude of the electric field component along the length of the rod is 12pdBdtCThe magnitude of the electric field component perpendicular to the rod is zeroDThe induced emf is 12lpdBdt.
AThe magnitude of the electric field created is 12rdBdtBThe magnitude of the electric field component along the length of the rod is 12pdBdtCThe magnitude of the electric field component perpendicular to the rod is zeroDThe induced emf is 12lpdBdt.a uniform magnetic field of induction B fills a cylinderical volume of radius R. A rod AB of length 2l is placed as shown in . If B changing at the rate dB/dt, the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
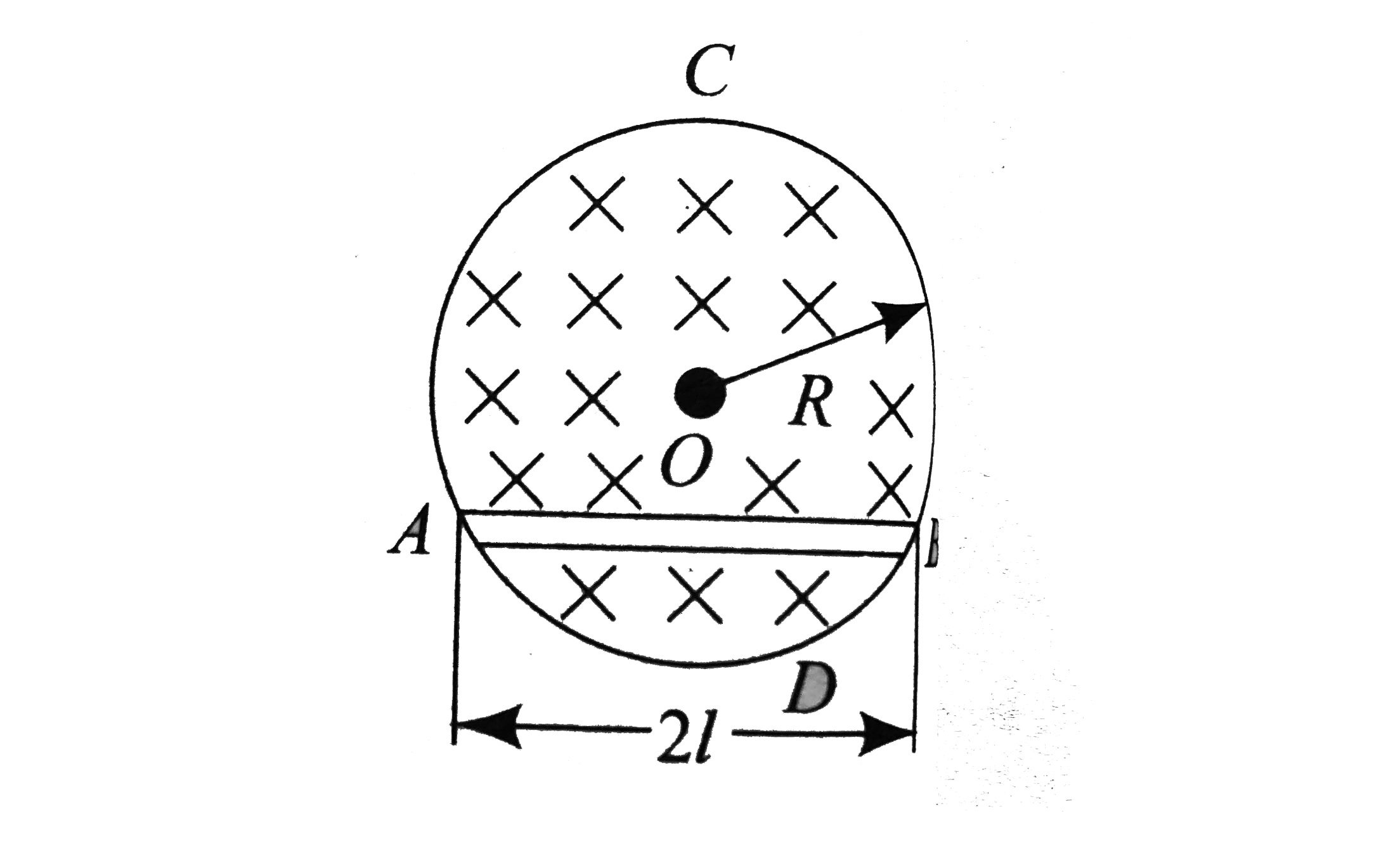 A(a) dBdtl√R2−l2B(b) dBdtl√R2+l2C( c) 12dBdtl√R2−l2D(d) 12dBdtl√R2+l2
A(a) dBdtl√R2−l2B(b) dBdtl√R2+l2C( c) 12dBdtl√R2−l2D(d) 12dBdtl√R2+l2Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.
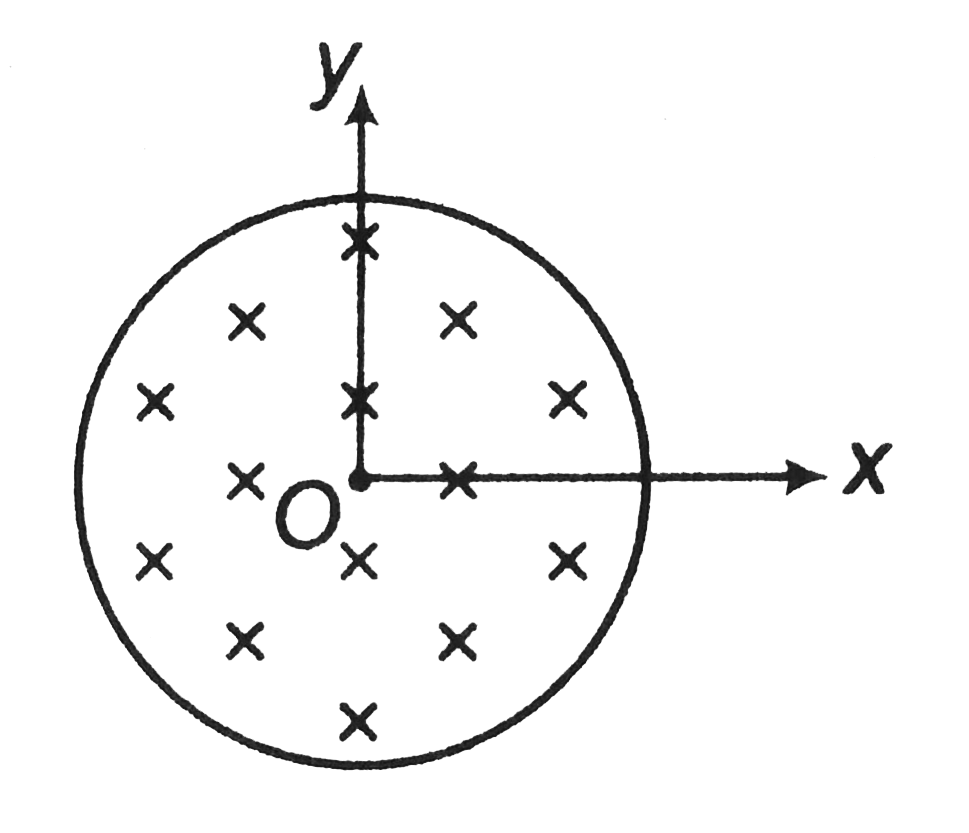 Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.

View SolutionA cylindrical region of radius R is filled with a uniform magnetic field B as shown in the figure. A metal wire (AB) of length L is placed inside the field such that its ends are symmetrically located with respect to the centre (O) of the circular cross section of the region. If the magnetic field is changed at a rate dBdt the emf induced in the metal wire is e. Find change in value of ε if the wire is displaced by a small distance ΔL parallel to its own length. Assume that the wire remains inside the field region.

View SolutionA uniform magnetic field B=B0t (where B0 is a positive constant) fills a cylindrical volume of radius R then the potential difference in the conducting rod PQ due to electrostatic field is :
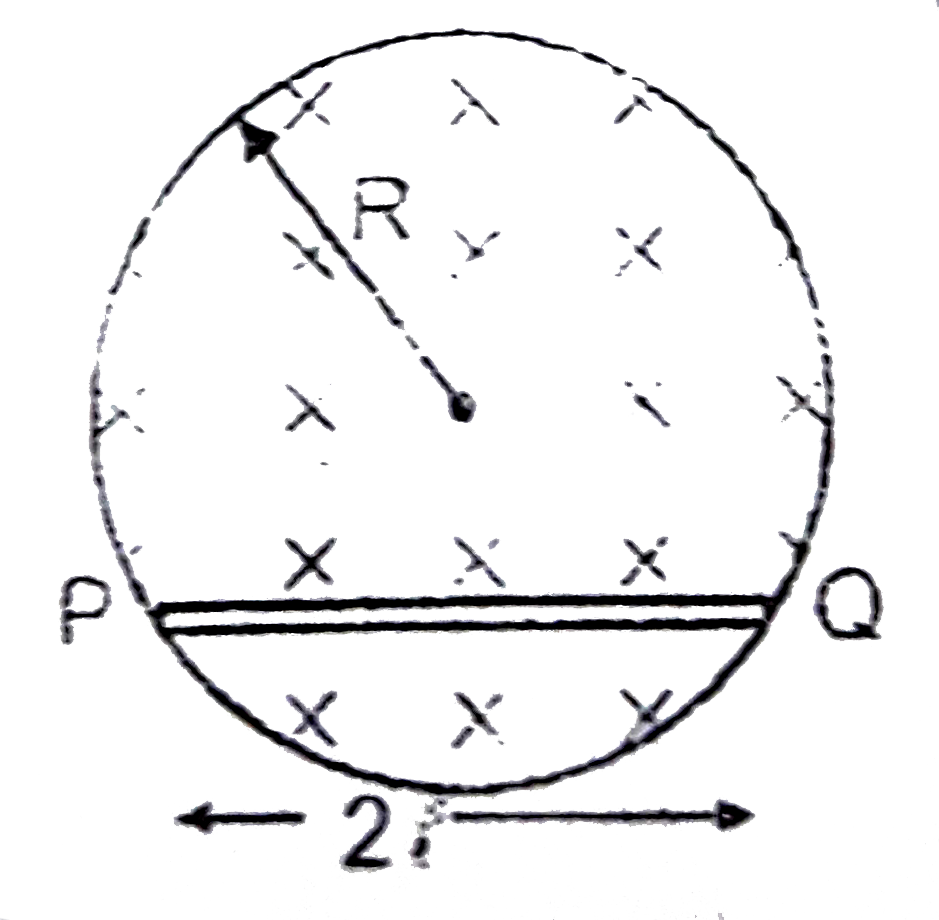
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform magnetic field B=B0t (where B0 is a positive constant) fills a cylindrical volume of radius R then the potential difference in the conducting rod PQ due to electrostatic field is :
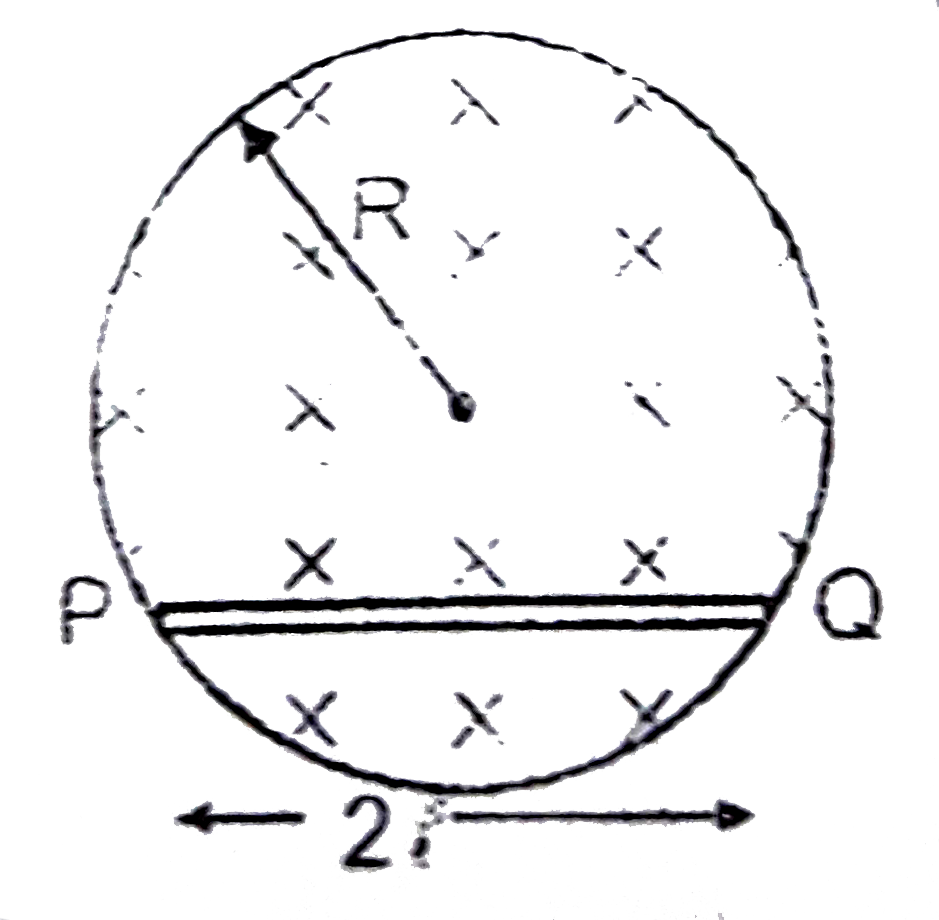
View Solution
