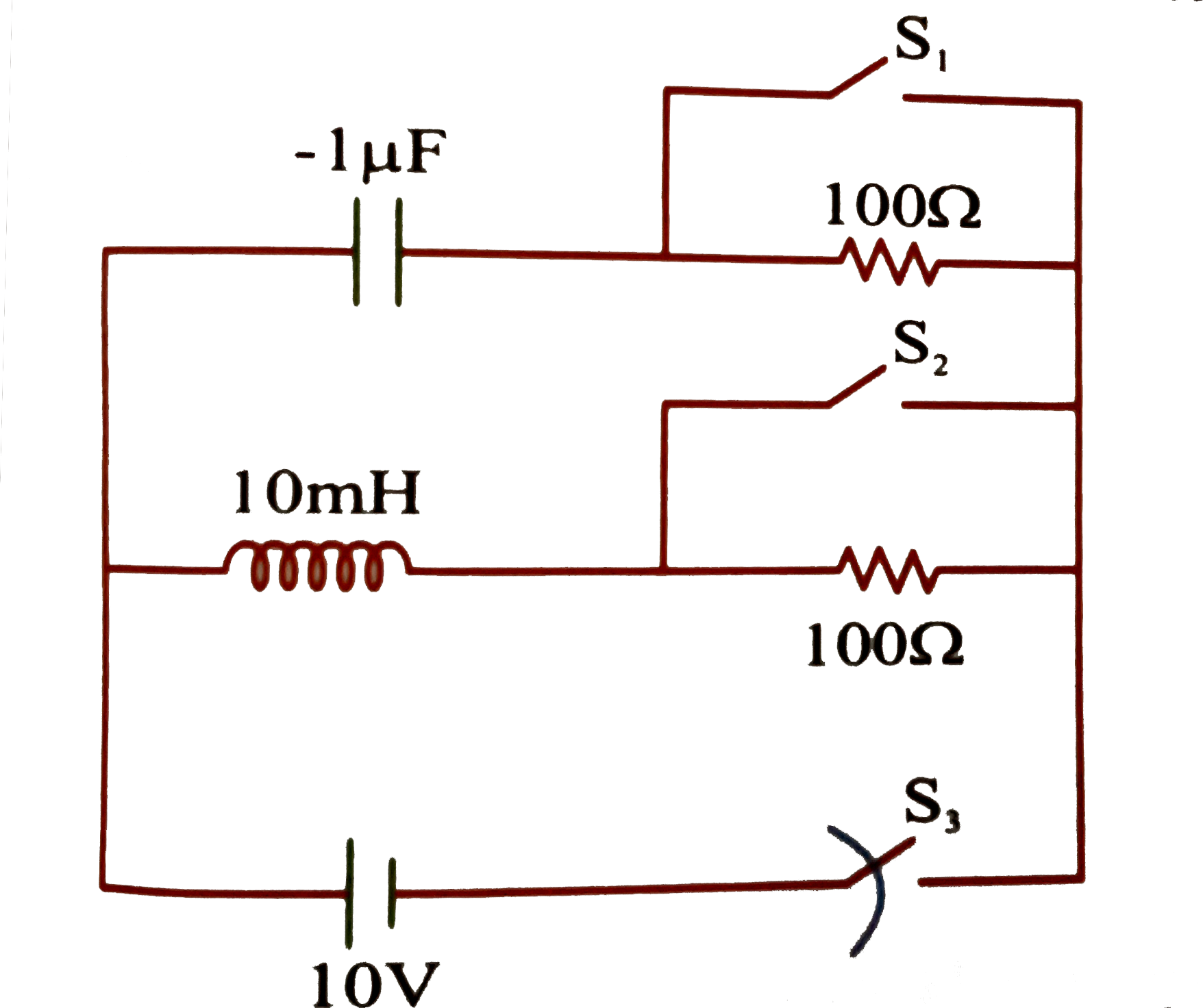
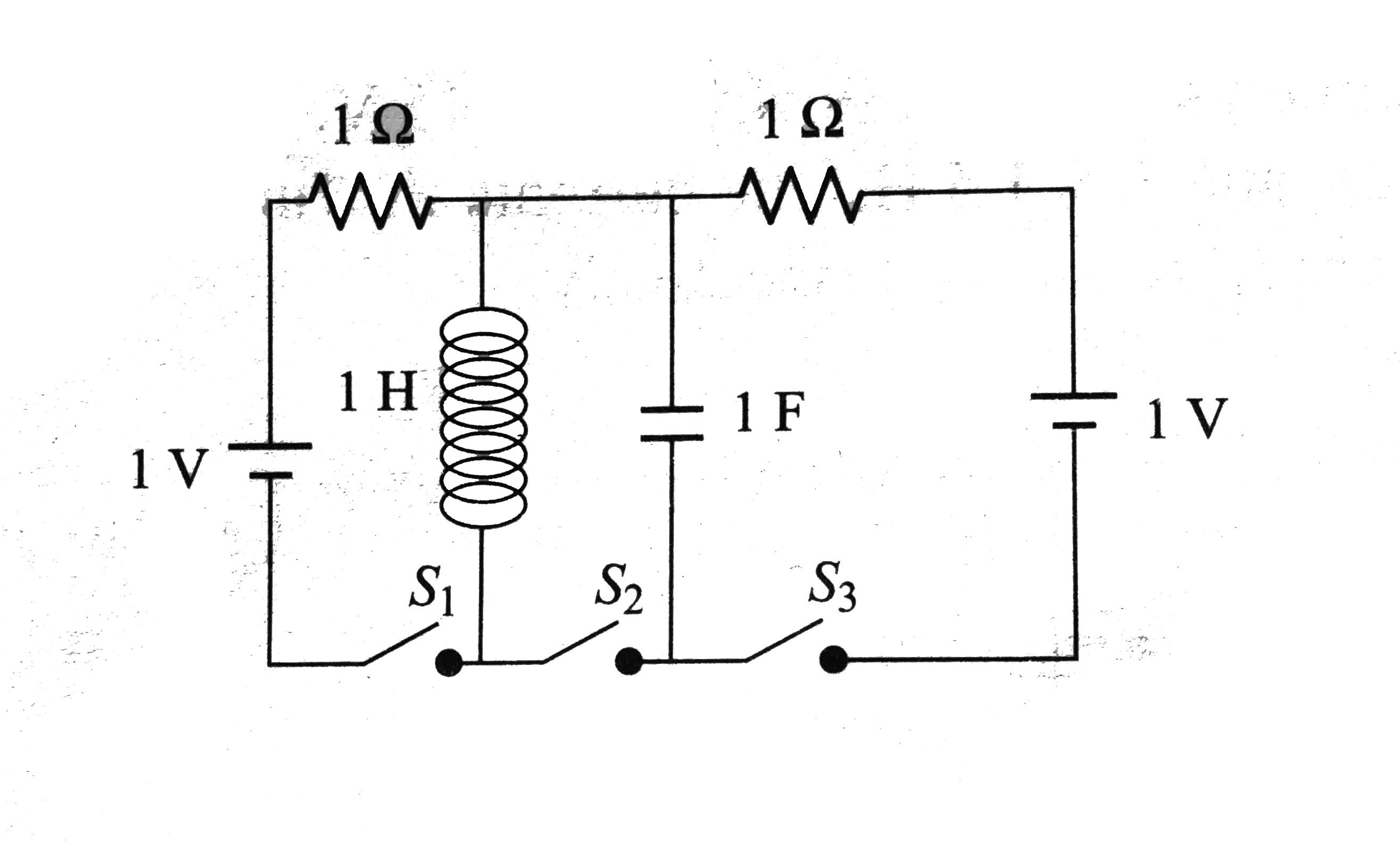
Switches S1,S2 remain open and switch S3 remains closed for long time such that capacitor becomes fully charged and current in inductor coil becomes maximum, Now switches S1,S2 are simultaneously closed andS3 in simultaneously opened at t=0
Assume that battery and inductor coil are ideal
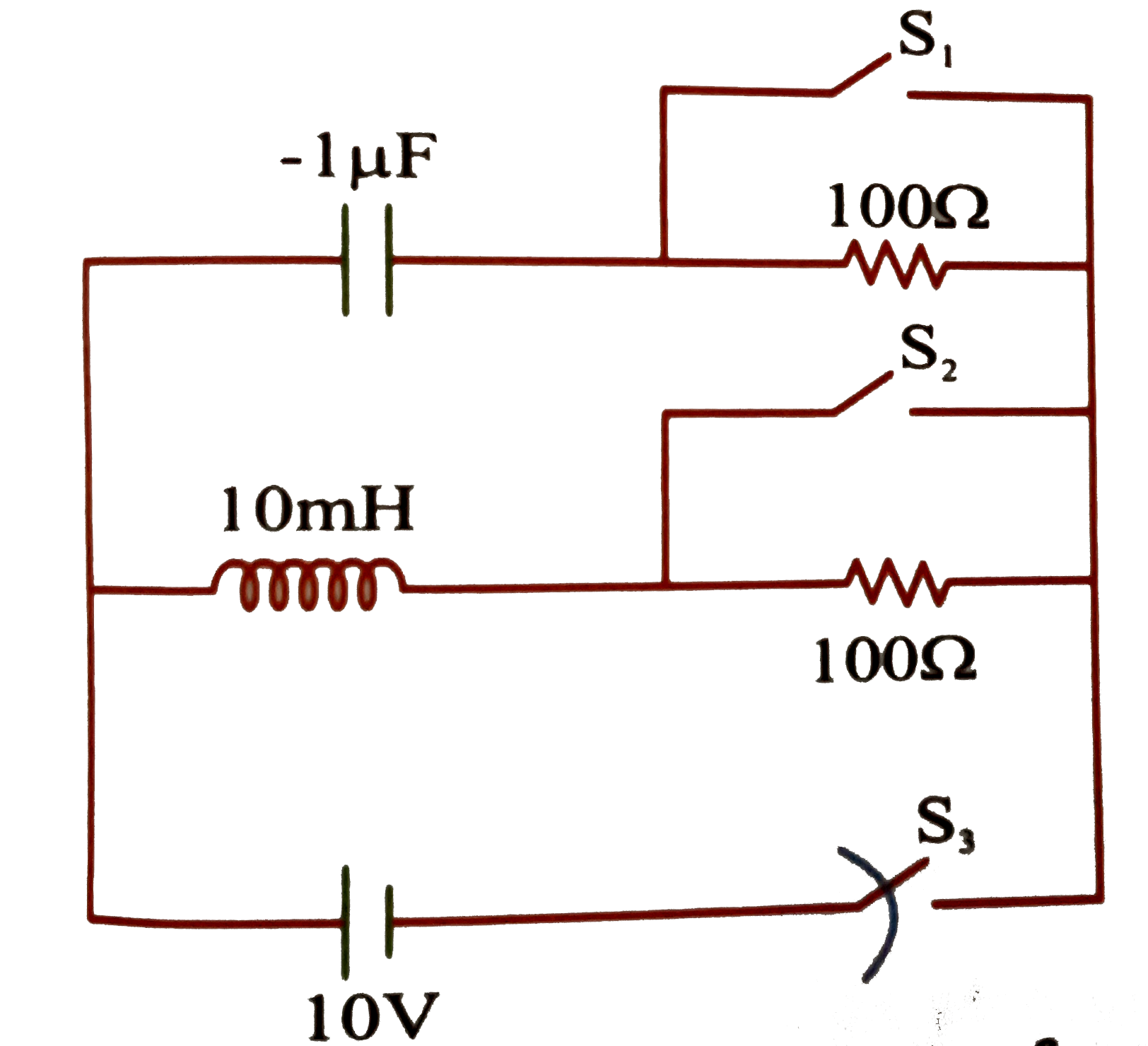
Charge (in μC) on capacitor as a function of time is :
q=10√2sin[104t+3π4]
q=10sin[104t+3π4]
q=10sin[102t+3π4]
q=10√2sin[102t+3π4]
The correct Answer is:A
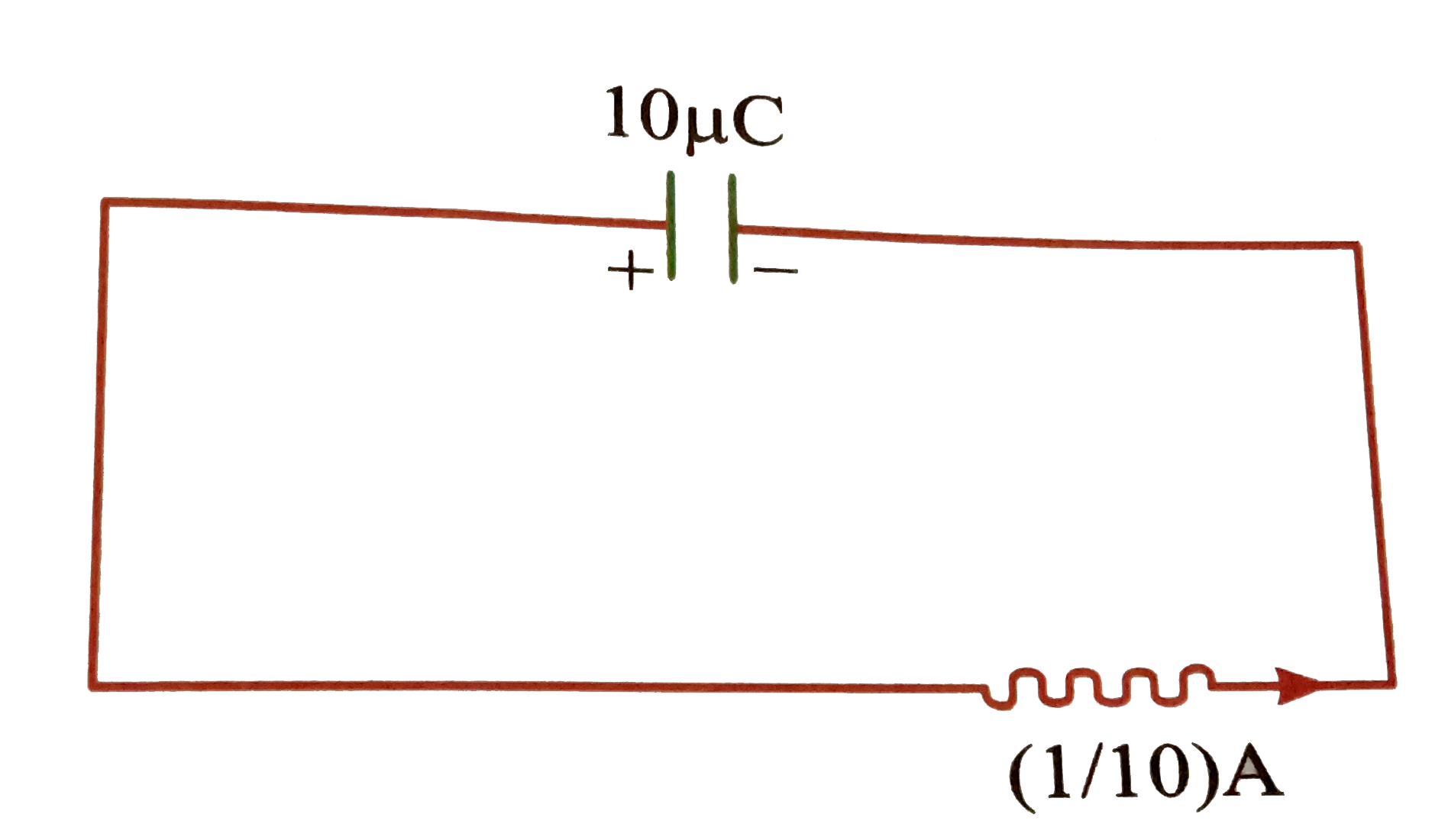
12Q20C=12Q2C+12Li⇒Q0=10√2μC
ω=1√LC=104 and Q=Q0√2 [Capacitor is discharging]
⇒q=10√2sin(104t+3π4)
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -VI
13 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Integer type questions
2 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -V
11 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
Knowledge Check
Switches S1,S2 remain open and switch S3 remains closed for long time such that capacitor becomes fully charged and current in inductor coil becomes maximum, Now switches S1,S2 are simultaneously closed andS3 in simultaneously opened at t=0
Assume that battery and inductor coil are ideal
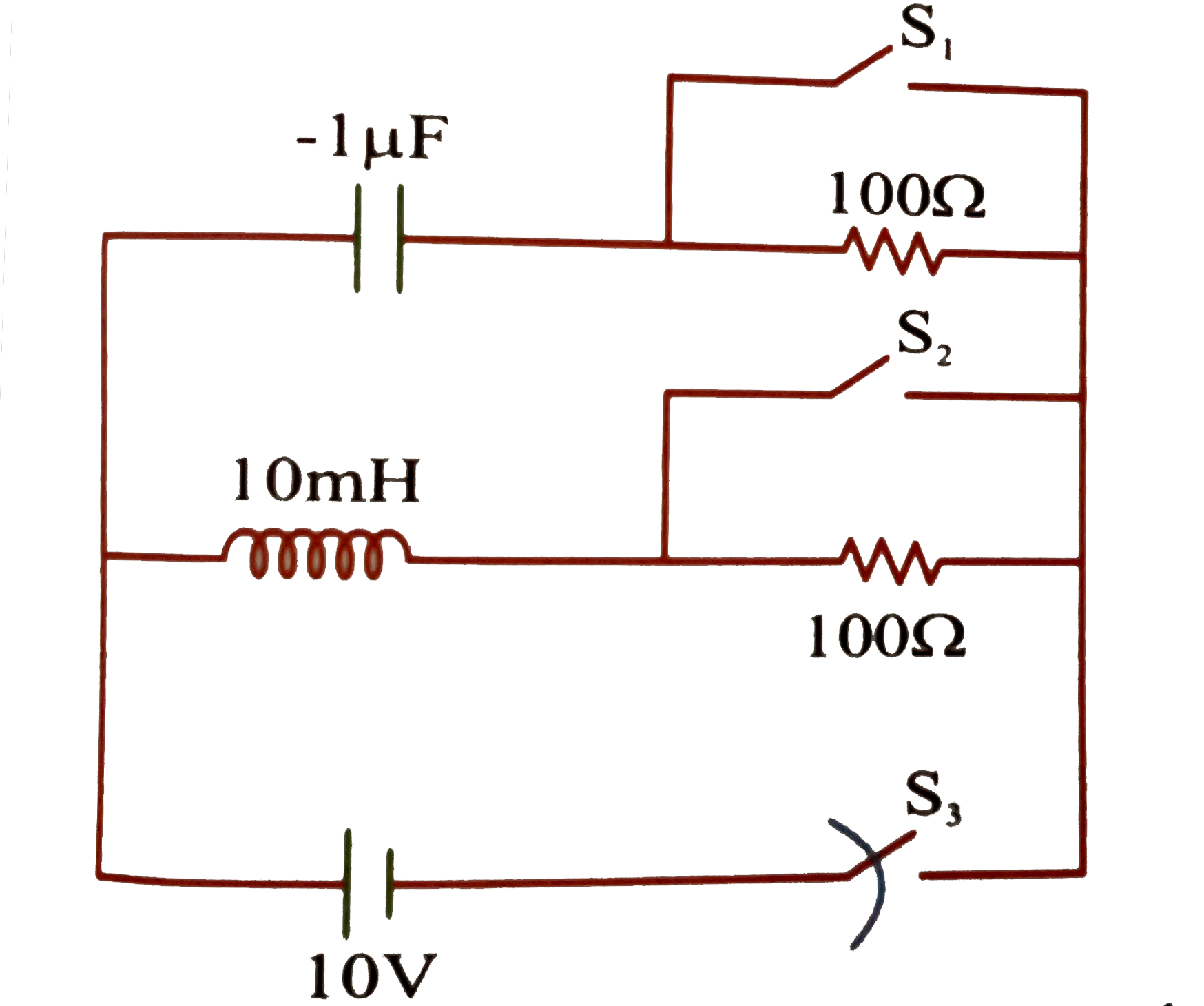
Maximum current in the inductor coil at any times t>0A110AB15√2AC15AD1ASwitches S1,S2 remain open and switch S3 remains closed for long time such that capacitor becomes fully charged and current in inductor coil becomes maximum, Now switches S1,S2 are simultaneously closed andS3 in simultaneously opened at t=0
Assume that battery and inductor coil are ideal
Find time t>0, when energy store in inductor would have minimum for the first time ?Aπ4×10−4sBπ4×10−4sC3π4×10−4sDπ×10−4sIn Fig. switch S is closed for a long time. At t=0, if it is opened, then
 Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
The circuit shown in figure is in the steady state with switch S1 closed. At t=0, S1 is opened and switch S2 is closed.

Find the first instant t, when energy in inductor becomes one third of that in capacitor
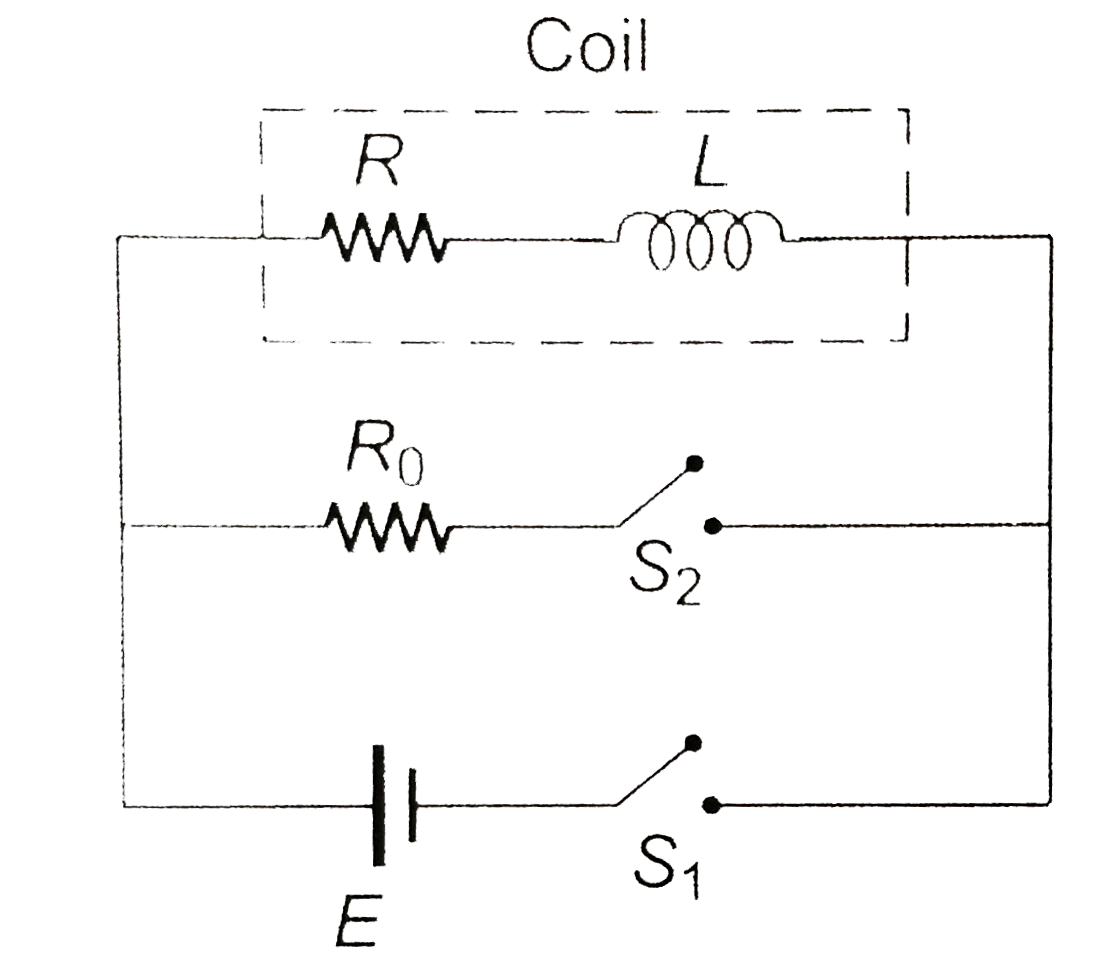
View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
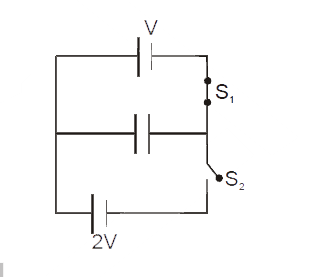
View SolutionAt any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
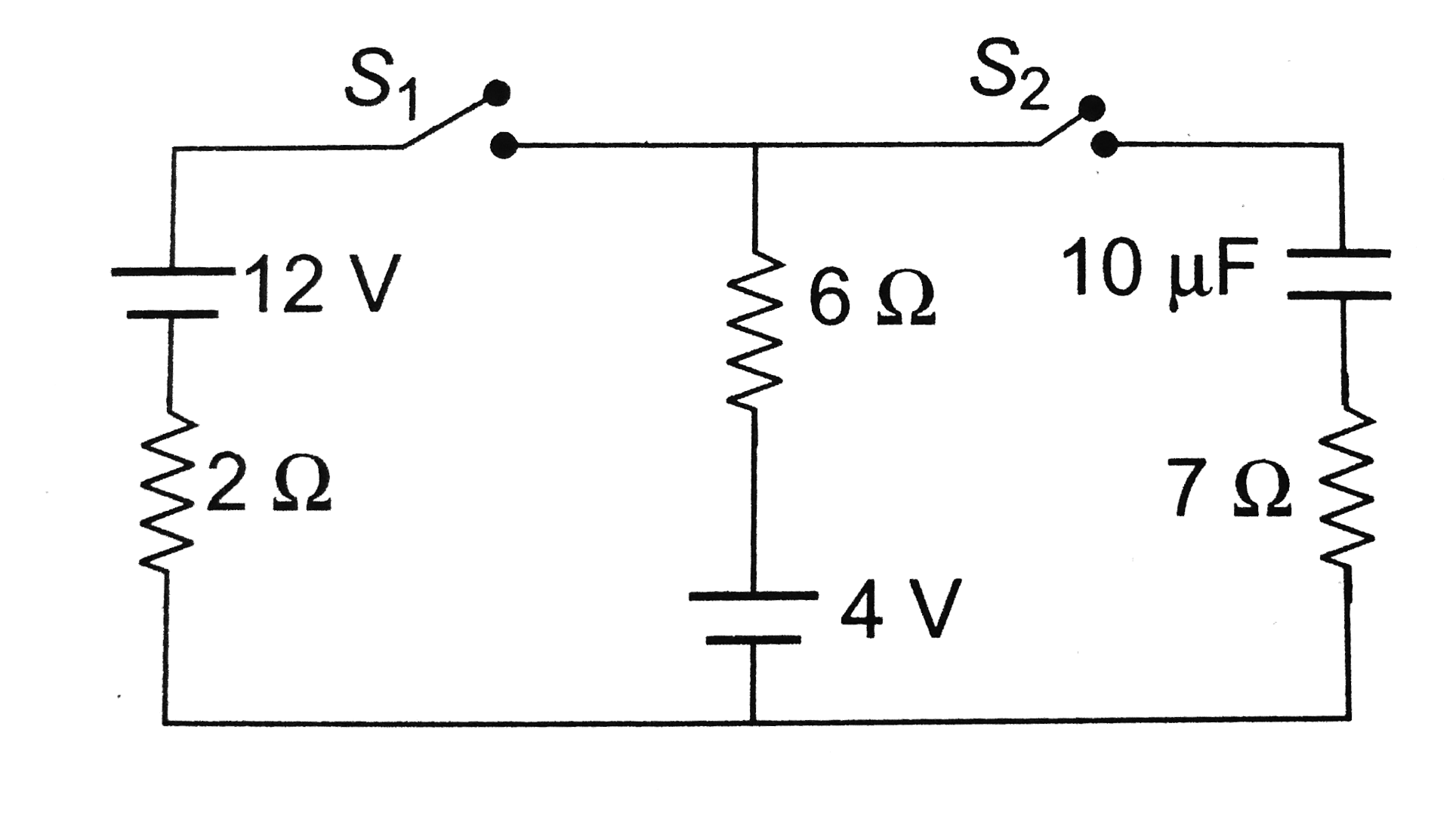
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the charge on the upper plate of the capacitor as a funtion of time
View Solution