A motor boat is to reach at point 30∘ upsteam (w.rt. Normal) on other side of a river flowing with velocity 5m/s. Velocity of motorboat w.r.t. water is 5√3m/s. The driver should steer the baot at an angular
120∘w.r.t. stream direction
30∘ w.r.t. normal to the bank
30∘ w.r.t. the line of destination form starting point.
none of these
The correct Answer is:C
To solve the problem of the motorboat reaching a point 30 degrees upstream while navigating a river flowing at 5 m/s, we can break down the problem into steps.
1. Identify Given Values:
- Velocity of the river, Vr=5m/s
- Velocity of the motorboat w.r.t water, Vb=5√3m/s
- Angle to reach upstream, θ=30∘
2. Set Up the Coordinate System:
- Let the positive x-direction be downstream (in the direction of the river flow).
- Let the positive y-direction be perpendicular to the river flow (across the river).
3. Break Down the Velocity of the Motorboat:
- The velocity of the motorboat can be broken down into two components:
- Vbx=Vb⋅cos(θ) (upstream component)
- Vby=Vb⋅sin(θ) (across the river component)
4. Account for the River's Velocity:
- The effective velocity of the boat upstream must counteract the river's flow. Thus, the net upstream velocity Vnet can be expressed as:
Vnet=Vbx−Vr
- For the boat to reach the target point at a 30-degree angle upstream, we need the ratio of the vertical and horizontal components of the boat's velocity to satisfy:
tan(30∘)=VbyVnet
5. Substituting Values:
- We know that tan(30∘)=1√3.
- Therefore, we can write:
1√3=VbyVbx−Vr
6. Expressing Components:
- Substitute the expressions for Vby and Vbx:
Vby=Vb⋅sin(θ)=5√3⋅sin(θ)
Vbx=Vb⋅cos(θ)=5√3⋅cos(θ)
- Thus, the equation becomes:
1√3=5√3⋅sin(θ)5√3⋅cos(θ)−5
7. Simplifying the Equation:
- Cancel 5√3 from both sides:
1√3=sin(θ)cos(θ)−1
- Cross-multiplying gives:
cos(θ)−1=√3sin(θ)
8. Using Trigonometric Identities:
- Rearranging gives:
cos(θ)−√3sin(θ)=1
- This equation can be solved for θ.
9. Finding the Angle θ:
- Solving the equation will yield θ=30∘.
Final Answer:
The driver should steer the boat at an angle of 30∘ upstream.
- Velocity of the river, Vr=5m/s
- Velocity of the motorboat w.r.t water, Vb=5√3m/s
- Angle to reach upstream, θ=30∘
- Let the positive x-direction be downstream (in the direction of the river flow).
- Let the positive y-direction be perpendicular to the river flow (across the river).
- The velocity of the motorboat can be broken down into two components:
- Vbx=Vb⋅cos(θ) (upstream component)
- Vby=Vb⋅sin(θ) (across the river component)
- The effective velocity of the boat upstream must counteract the river's flow. Thus, the net upstream velocity Vnet can be expressed as:
Vnet=Vbx−Vr
- For the boat to reach the target point at a 30-degree angle upstream, we need the ratio of the vertical and horizontal components of the boat's velocity to satisfy:
tan(30∘)=VbyVnet
- We know that tan(30∘)=1√3.
- Therefore, we can write:
1√3=VbyVbx−Vr
- Substitute the expressions for Vby and Vbx:
Vby=Vb⋅sin(θ)=5√3⋅sin(θ)
Vbx=Vb⋅cos(θ)=5√3⋅cos(θ)
- Thus, the equation becomes:
1√3=5√3⋅sin(θ)5√3⋅cos(θ)−5
- Cancel 5√3 from both sides:
1√3=sin(θ)cos(θ)−1
- Cross-multiplying gives:
cos(θ)−1=√3sin(θ)
- Rearranging gives:
cos(θ)−√3sin(θ)=1
- This equation can be solved for θ.
- Solving the equation will yield θ=30∘.
The driver should steer the boat at an angle of 30∘ upstream.
Similar Questions
Calculate the velocity head of water which is flowing with a velocity of 5 m/s in a horizontal pipe.
View SolutionA boat is moving with a velocity 3ˆi−4ˆj w.r.t ground. The water in the river is moving with a velocity −3ˆi−4ˆj w.r.t ground. What is the relative velocity of boat w.r.t water.
View Solution
Knowledge Check
- Question 1 - Select One or More
A motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
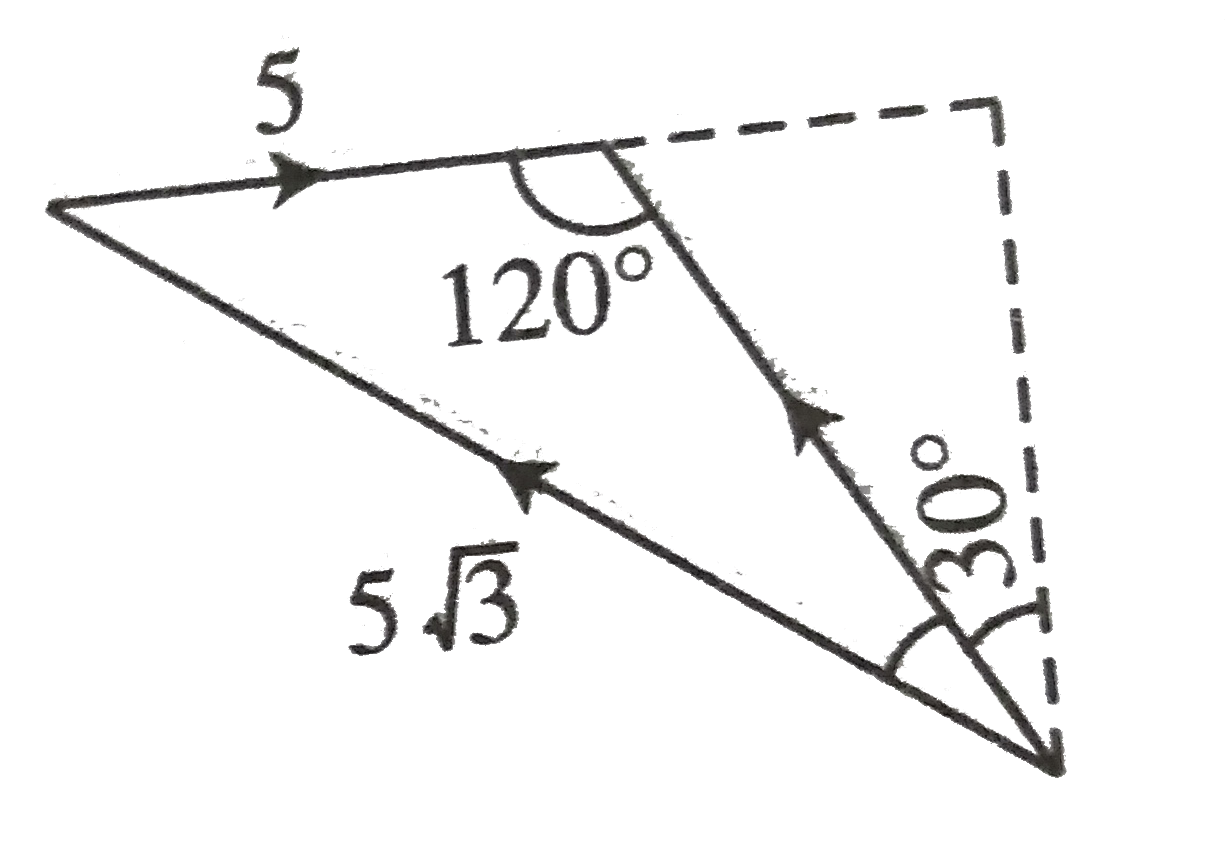 A30∘ up w.r.t the line of destination from the starting pointB60∘up w.r.t normal to the bankC150∘ w.r.t stream directionDnone of these
A30∘ up w.r.t the line of destination from the starting pointB60∘up w.r.t normal to the bankC150∘ w.r.t stream directionDnone of these - Question 2 - Select One
A motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
 A30∘ w.r.t. the line of destination from the starting point.B60∘ w.r.t. normal to the bank.C120∘ w.r.t. stream directionDNone of these
A30∘ w.r.t. the line of destination from the starting point.B60∘ w.r.t. normal to the bank.C120∘ w.r.t. stream directionDNone of these - Question 3 - Select One
A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
AThe direction of boat's velocity is 30∘ west of north.BThe direction of boat's velocity is north - west.CResultant velocity is 5ms−1.DResultant velocity of boat is 5√2ms−1.
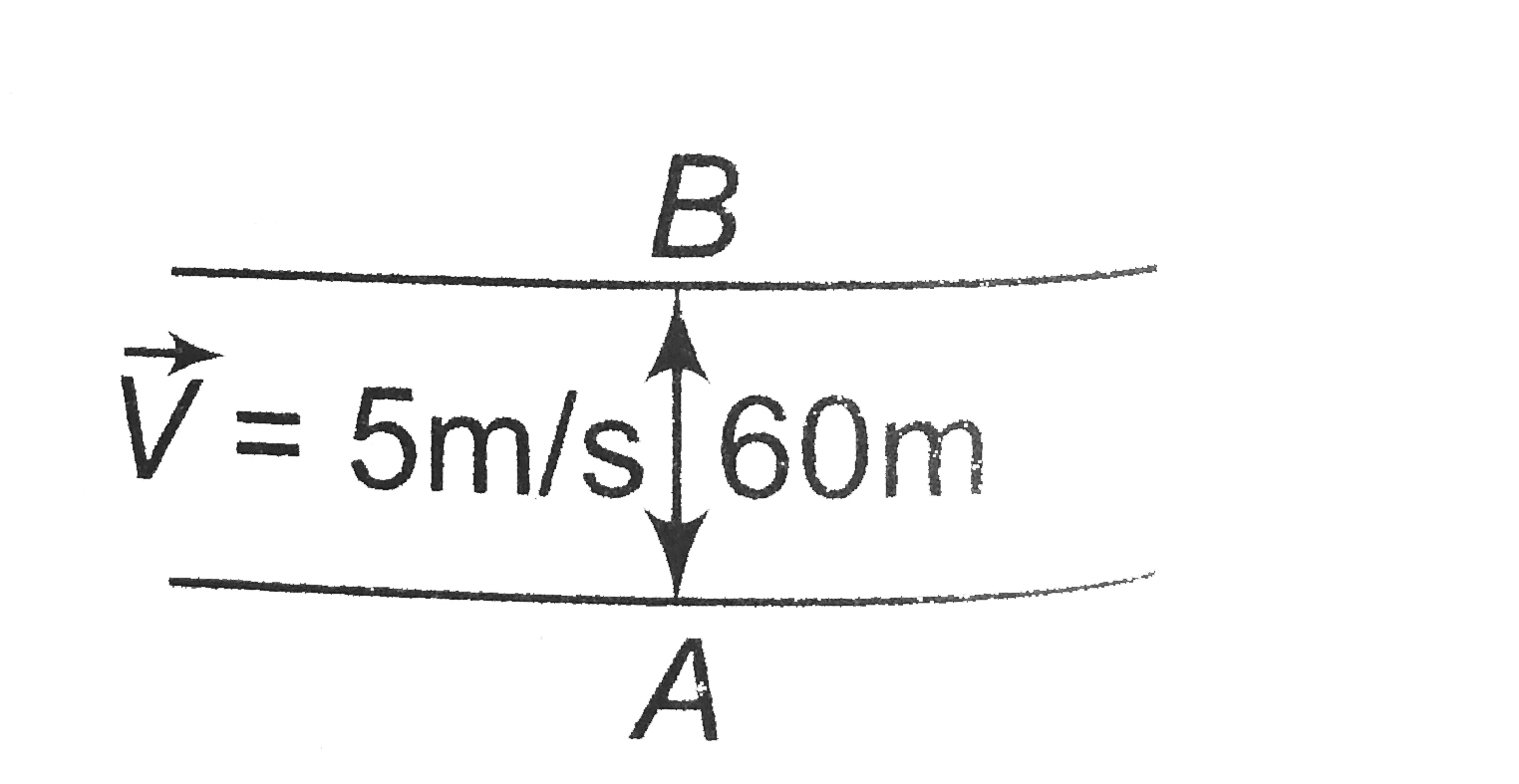
A man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
 View Solution
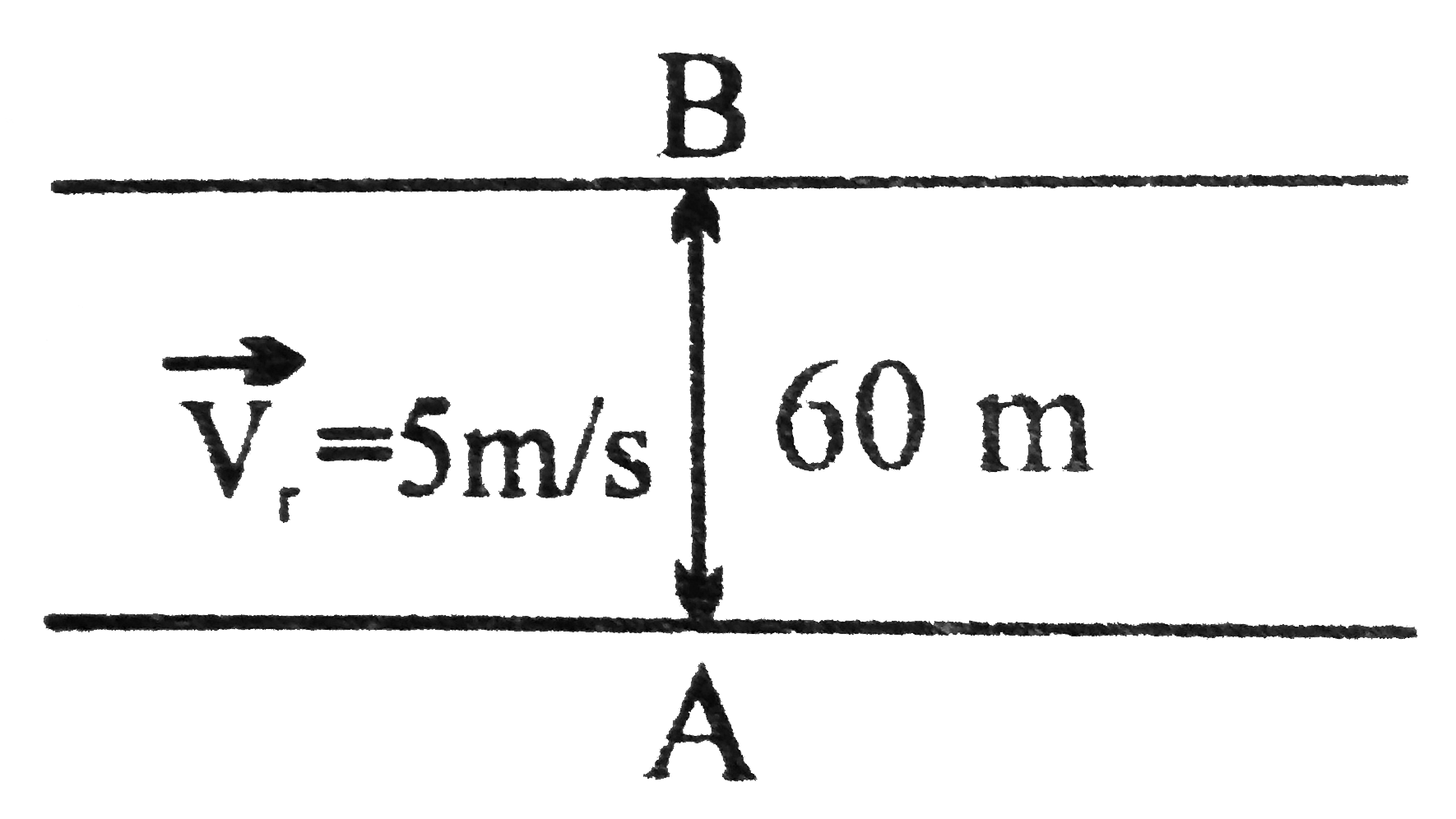
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
 View Solution
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA boat of mass 50kg is at rest. A dog of mass 5kg moves in the boat with a velocity of 20m/s. What is the velocity of boat?
View SolutionA boat is moving towards east velocity 4 m/s w.r.t still water and river is flowing towards north with velocity 2 m/s and the wind blowing towards north with velocity 6 m/s. the direction of the flag blown over by the wind hpisted on the boat is
View Solution

