A river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
8 m/s
10 m/s
6 m/s
5 m/s
The correct Answer is:b
To solve the problem, we will use the concept of relative velocity and the Pythagorean theorem.
1. Identify the Given Values:
- Width of the river (d) = 80 m
- Velocity of the river (Vr) = 6 m/s
- Time taken to cross the river (t) = 10 s
2. Calculate the Velocity of the Motorboat Across the River:
- The distance across the river is the width of the river.
- The speed of the motorboat in the direction perpendicular to the river (Vb_perpendicular) can be calculated using the formula:
Vbperpendicular=DistanceTime=80 m10 s=8 m/s
3. Set Up the Vector Relationship:
- The velocity of the motorboat (Vb) can be broken down into two components:
- One component is perpendicular to the river (Vb_perpendicular = 8 m/s).
- The other component is parallel to the river (Vb_parallel = Vr = 6 m/s).
- Since these two components are perpendicular to each other, we can use the Pythagorean theorem to find the resultant velocity of the motorboat in still water (Vb_total):
Vbtotal=√(Vbperpendicular)2+(Vbparallel)2
Vbtotal=√(8 m/s)2+(6 m/s)2
Vbtotal=√64+36=√100=10 m/s
4. Conclusion:
- The velocity of the motorboat in still water is 10 m/s.
- Width of the river (d) = 80 m
- Velocity of the river (Vr) = 6 m/s
- Time taken to cross the river (t) = 10 s
- The distance across the river is the width of the river.
- The speed of the motorboat in the direction perpendicular to the river (Vb_perpendicular) can be calculated using the formula:
Vbperpendicular=DistanceTime=80 m10 s=8 m/s
- The velocity of the motorboat (Vb) can be broken down into two components:
- One component is perpendicular to the river (Vb_perpendicular = 8 m/s).
- The other component is parallel to the river (Vb_parallel = Vr = 6 m/s).
- Since these two components are perpendicular to each other, we can use the Pythagorean theorem to find the resultant velocity of the motorboat in still water (Vb_total):
Vbtotal=√(Vbperpendicular)2+(Vbparallel)2
Vbtotal=√(8 m/s)2+(6 m/s)2
Vbtotal=√64+36=√100=10 m/s
- The velocity of the motorboat in still water is 10 m/s.
Similar Questions
Water is flowing in a river of width 36m with a speed of 2ms−1 .A person in a boat at a point "P" on the bank of the river wants to cross the river by the shortest path to reach a point "Q" directly opposite on the other bank.If he can row his boat with a speed of 4ms−1 in still water,he should row his boat at an angle of ?
View Solution[" 16.Water is flowing in a river of width "36m" with a speed of "2ms^(-1)" .A person in a boat "],[" at a point "p" on the bank of the river wants to cross the river by the shortest path to "],[" reach a point "Q" directly opposite on the other bank.If he can row his boat with a "],[" speed of "4ms^(-1)" in still water,he should row his boat at an angle of (multiples of "],[10^(@)" ) "]
View Solution
Knowledge Check
- Question 1 - Select One
A man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
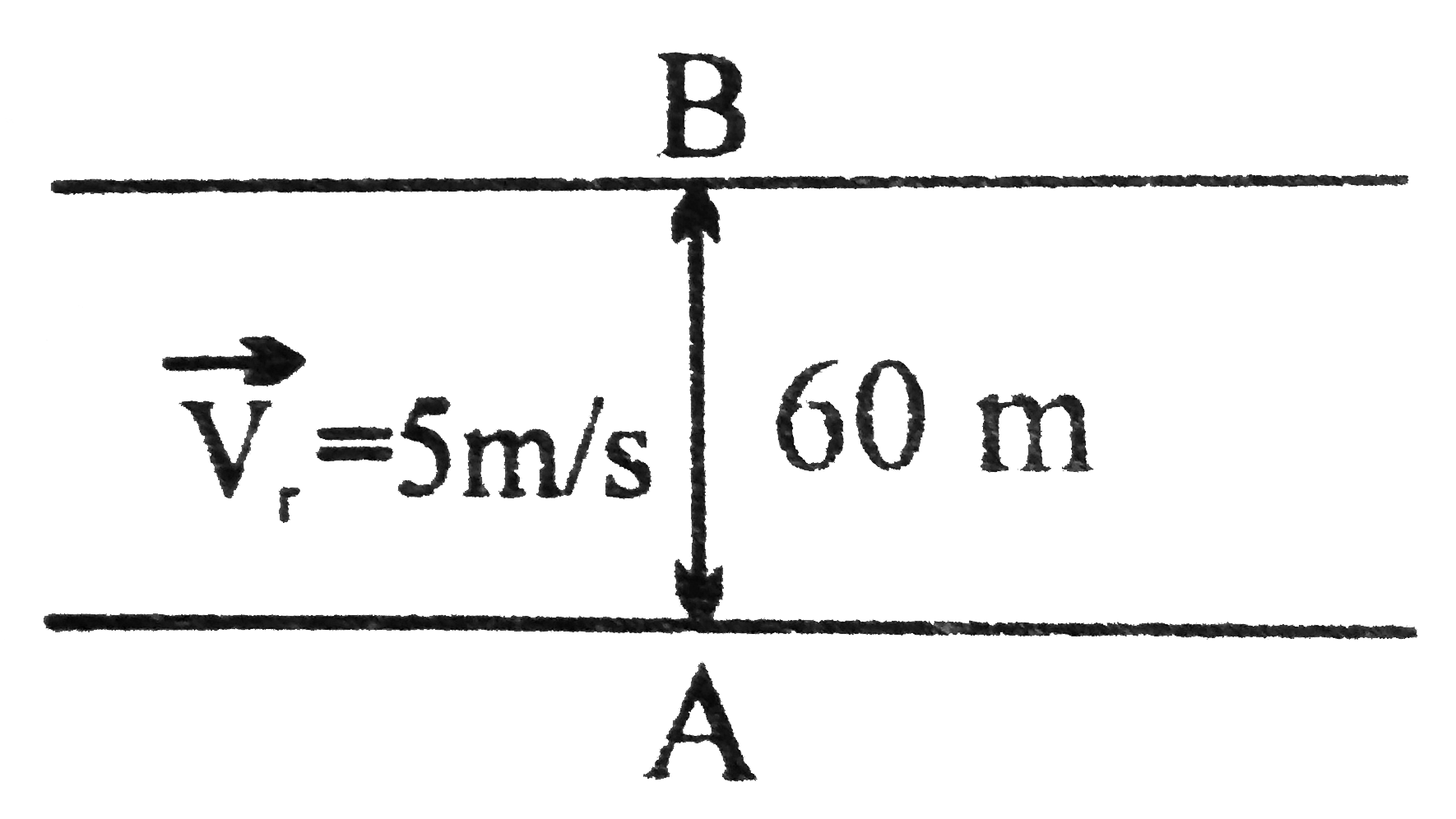 A12m/sB13m/sC5m/sD10m/s
A12m/sB13m/sC5m/sD10m/s - Question 2 - Select One
A man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
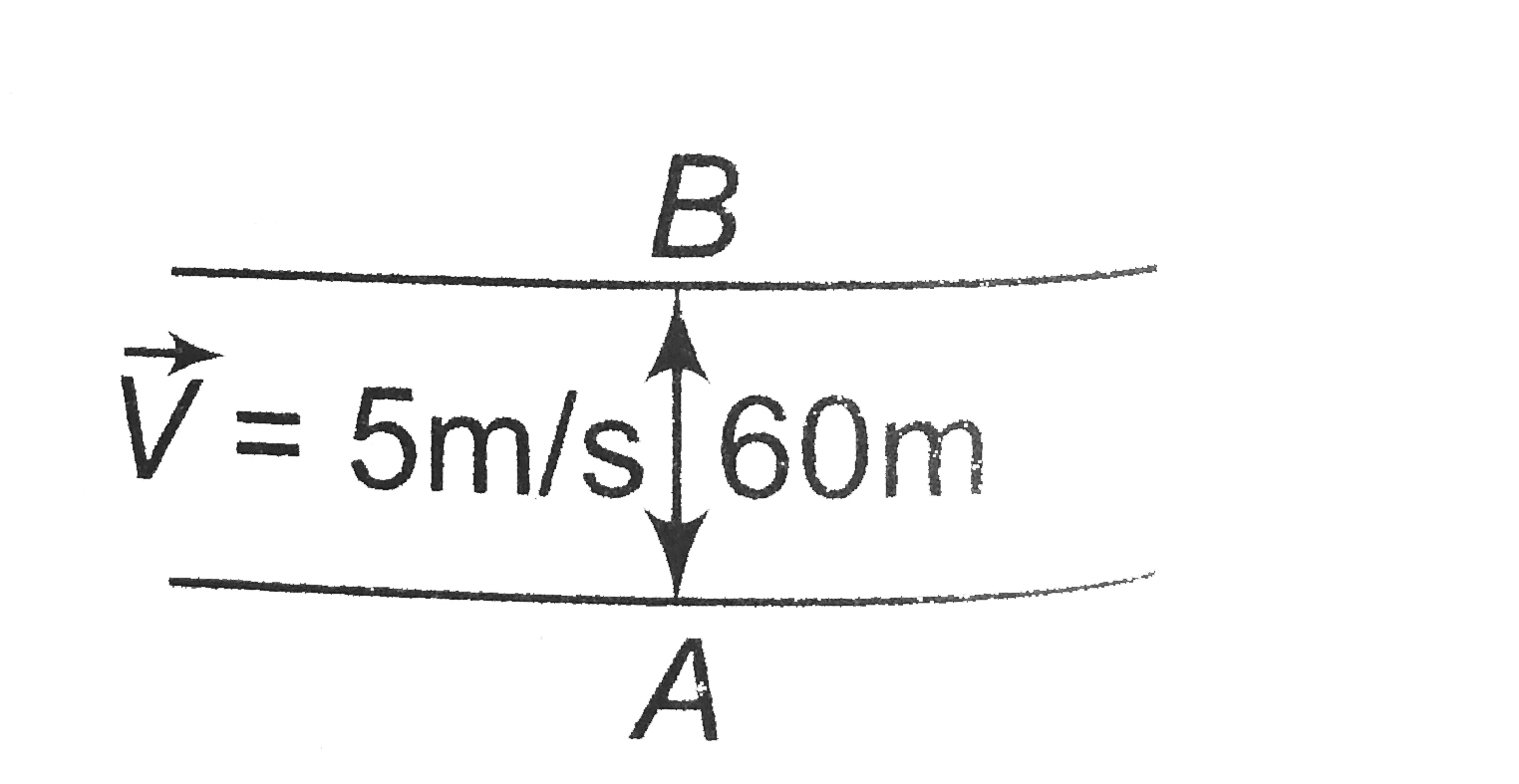 A12m/sB13m/sC5m/sD10m/s
A12m/sB13m/sC5m/sD10m/s - Question 3 - Select One or More
A man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
AMan can directly reach point B in time d/l.BMan can cross the river in minimum time d/vCMan can reach point B directly in time d√v2−u2DIf u>v then man cannot reach the point B directly .
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.View SolutionA man crosses a river in a boat. If he cross the river in minimum time he takes 10min with a drift 120m. If he crosses the river taking shortest path, he takes 12.5min, find
(a) width of the river
(b) velocity of the boat with respect to water
(c) speed of the currentView SolutionA river is flowing with a velocity of 2m/s. If the width of river in 100 m and swimmer wants to cross river is shortest time, what time (in sec) would he take if velocity of swimmer in still water is 4 m/s ?
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View Solution

