Moment of inertia of a thin semicircular disc (mass−M&radius=R) about an axis through point O and perpendicular to plane of disc, is given by :
 .
.
14MR2
12MR2
18MR2
MR2
The correct Answer is:B
Idisc=12(2M)R2
IHalfdisc=12MR2.
 .
.
Similar Questions
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate moment of inertia of a uniform circular disc of mass 700g and diameter 20cm about
(i) an axis through the centre of disc and perpendicular to its plane, (ii) a diameter of disc, (iii) a tangent in the plane of the disc, (iv) a tangent perpendicular to the plane of the disc.
View Solution
Knowledge Check
The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
AMR24BMR22CMR2D2MR2The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
AMR24BMR22CMR2D2MR2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
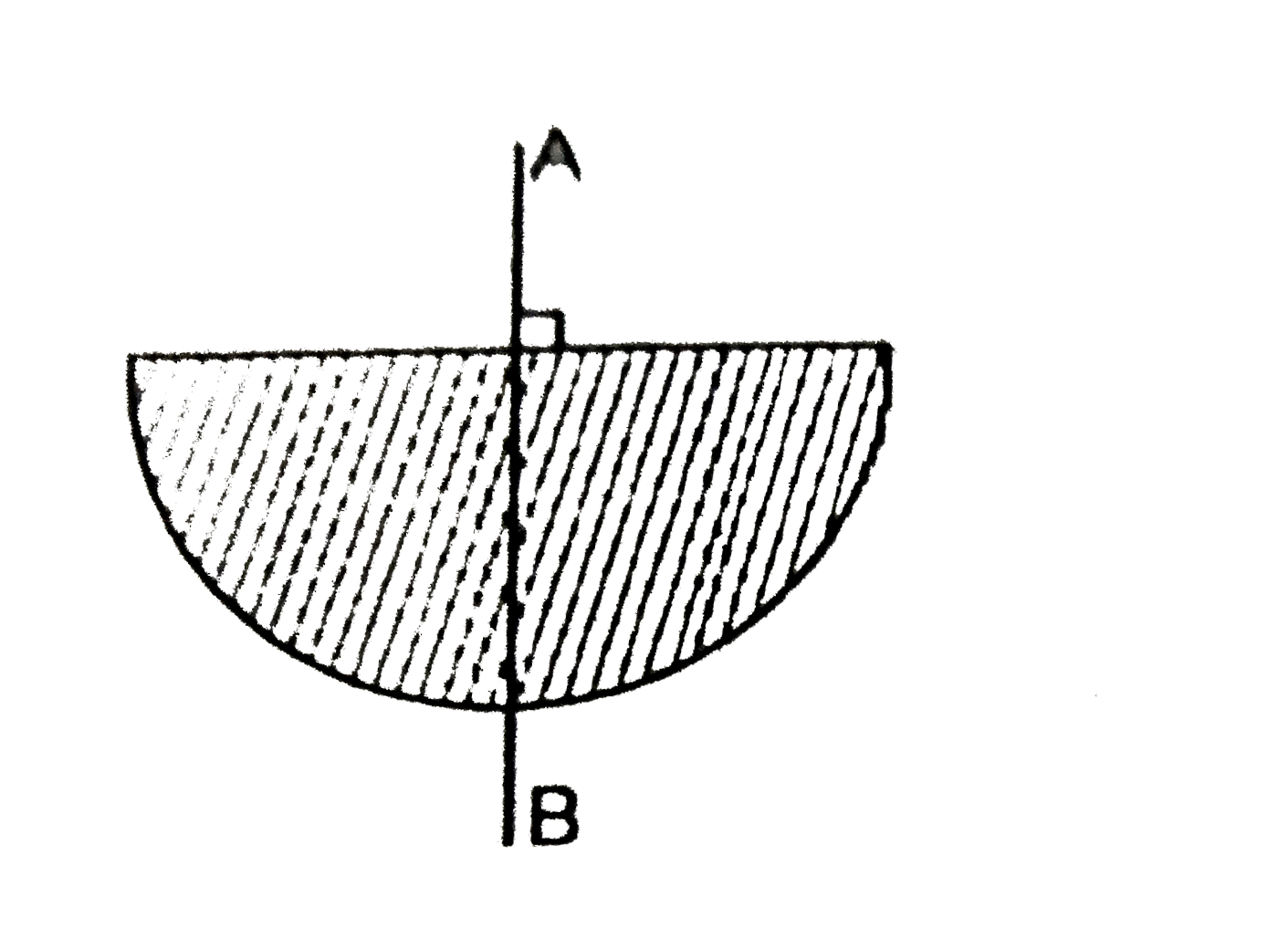
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View SolutionThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View Solution