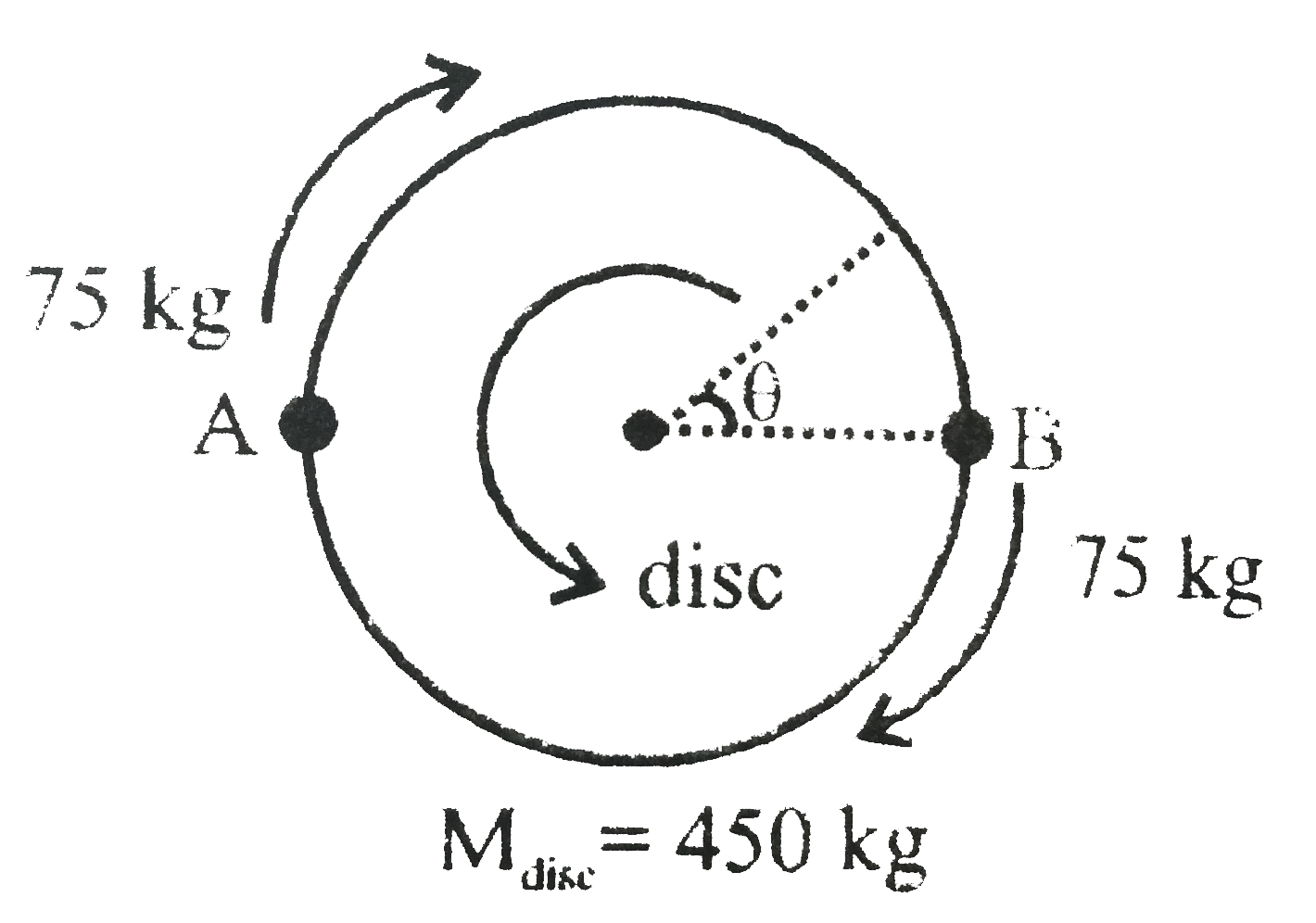
Two men, each of mass $75 k g$ , stand on the rim of a horizontal large disc, diametrically opposite to each other. The disc has a mass $450 k g$ and is free to rotate about its axis. Each man simultaneouslt start along the rim clockwise with the same speed and reaches their original starting points on the disc. Find the angle turned through by the disc with respect to the ground.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $4 π / 4$

$2 I_{1} ω_{1} = I_{disc} ω_{2}$
$2 \times 75 \times R^{2} \times \frac{(2 π - θ)}{T} = \frac{1}{2} \times 450 \times R^{2} \times \frac{θ}{T}$
$2 (2 π - θ) = 3 θ, θ = \frac{4 π}{5}$

Alternatively
$2 I ω_{m} + I_{d} ω_{d} = 0$
$2 (m R^{2}) ω_{m} = (\frac{1}{2} M_{d} R^{2}) ω_{d}$
$4 m ω_{m} = M_{d} ω_{d}$
$4 \times 75 ω_{m} = 450 ω_{d}$
$2 ω_{m} = 3 ω_{d}$ or $2 θ_{m} = 3 θ_{d}$ ....(1)
$θ_{m} + θ_{d} = 2 π$
$\frac{3 θ_{d}}{2} + θ_{d} = 2 π$ "from" (1) $θ_{d} = \frac{2 π \times 2}{5} = \frac{4 π}{5} r a d$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
Two men each of mass $m$ stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass $M$ and is free to rotate about a vertical axis passing through its centre of mass. Each man start simultaneously along the rim clockwise and reaches their original starting points on the disc. The angle turned through by the disc with respect to the ground (in radian) is:
A $\frac{8 m π}{4 m + M}$
B $\frac{2 m π}{4 m + M}$
C $\frac{m π}{M + m}$
D $\frac{4 m π}{2 M + m}$
Question 2 - Select One
Two men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each mass start simultaneously along the rim clockwise and reaches their original starting positions on the disc. The angle turned through by disc with respect to the ground (in radian) is
A $\frac{8 m π}{4 m + M}$
B $\frac{2 m π}{4 m + M}$
C $\frac{m π}{M + m}$
D $\frac{4 m π}{2 M + m}$
Question 3 - Select One
A disc of mass 1 kg and radius 10 cm is rotating about its axis with an anuglar velocity of 2 rad/s. The linear momentum of the disc,
A0.2 kg-m/s
Bzero
C0.4 kg-m/s
D0.02 kg-m/s

Recommended Questions

Home
Ask Doubt
Profile