A uniform wood door has mass m, height h, and width w. It is hanging from two hinges attached to one side , the hinges are located h/3 and 2h/3 form the bottom of the door. Suppose that m=20kg,h=2.20m, and the bottom smooth hinge is not screwed into the door frame. Find the forces acting on the door.
 .
.
The correct Answer is:Fd/x=3mgw2h and Fduy=mg
For balance of weight
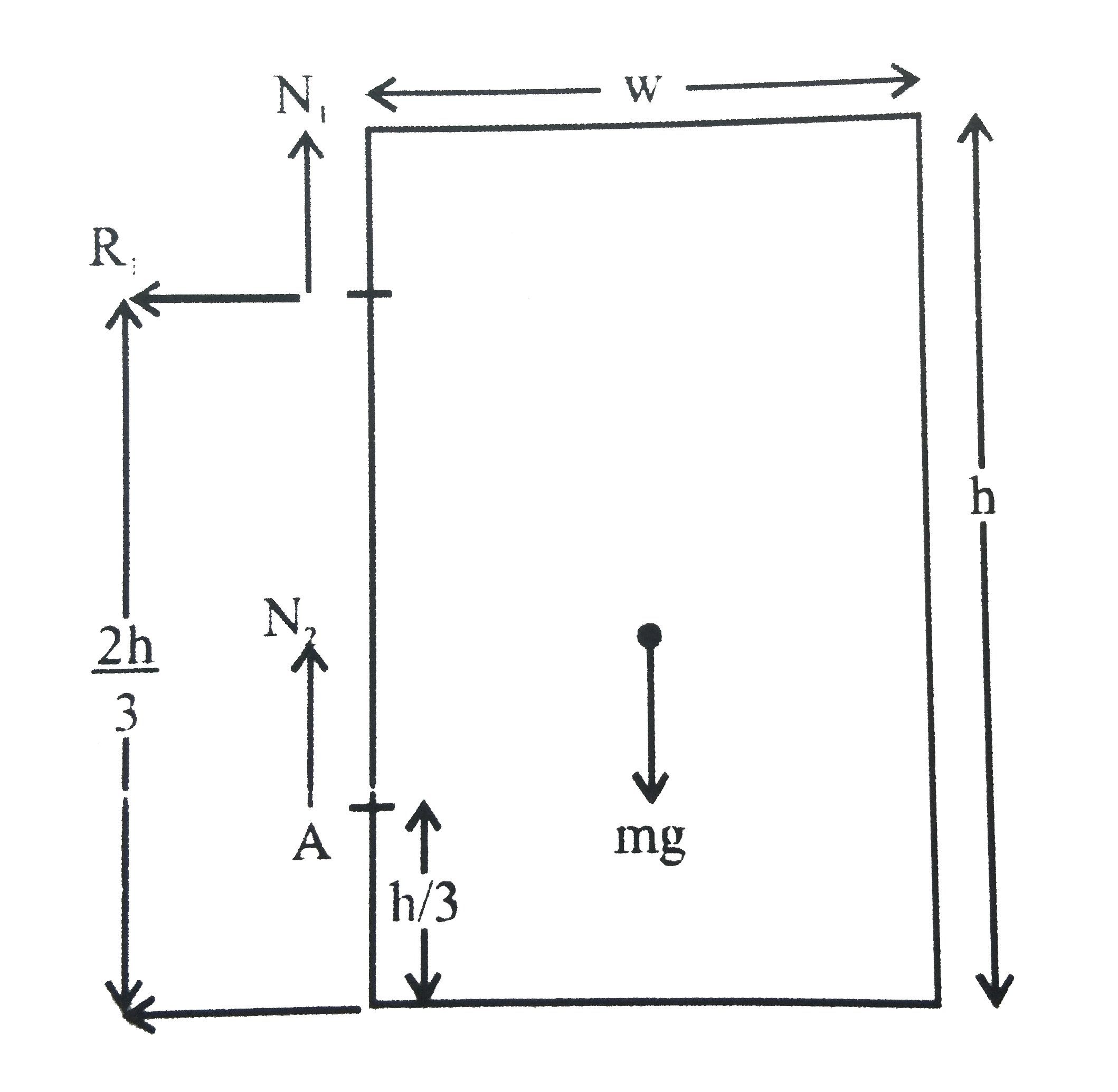
mg=N1+N2
Torque about A
R1×h3=mg×w2⇒R1=3mgw2h
Fx=3mgw2h and Fy=mg.
Similar Questions
A uniform wood panel of mass 35.0 kg is hinged ver tically on a wall by two hinges, one 0.300 m from its top and the other 0.300 m from its bottom. The panel is 2.10 m tall and 0.910 m wide. A y axis extends upward through the hinges and an x axis extends outward along the panel's width. If each hinge supports half the panel's weight, what are the forces on the panel at (a) the top hinge and (b) the bottom hinge, both in unit-vec notation?
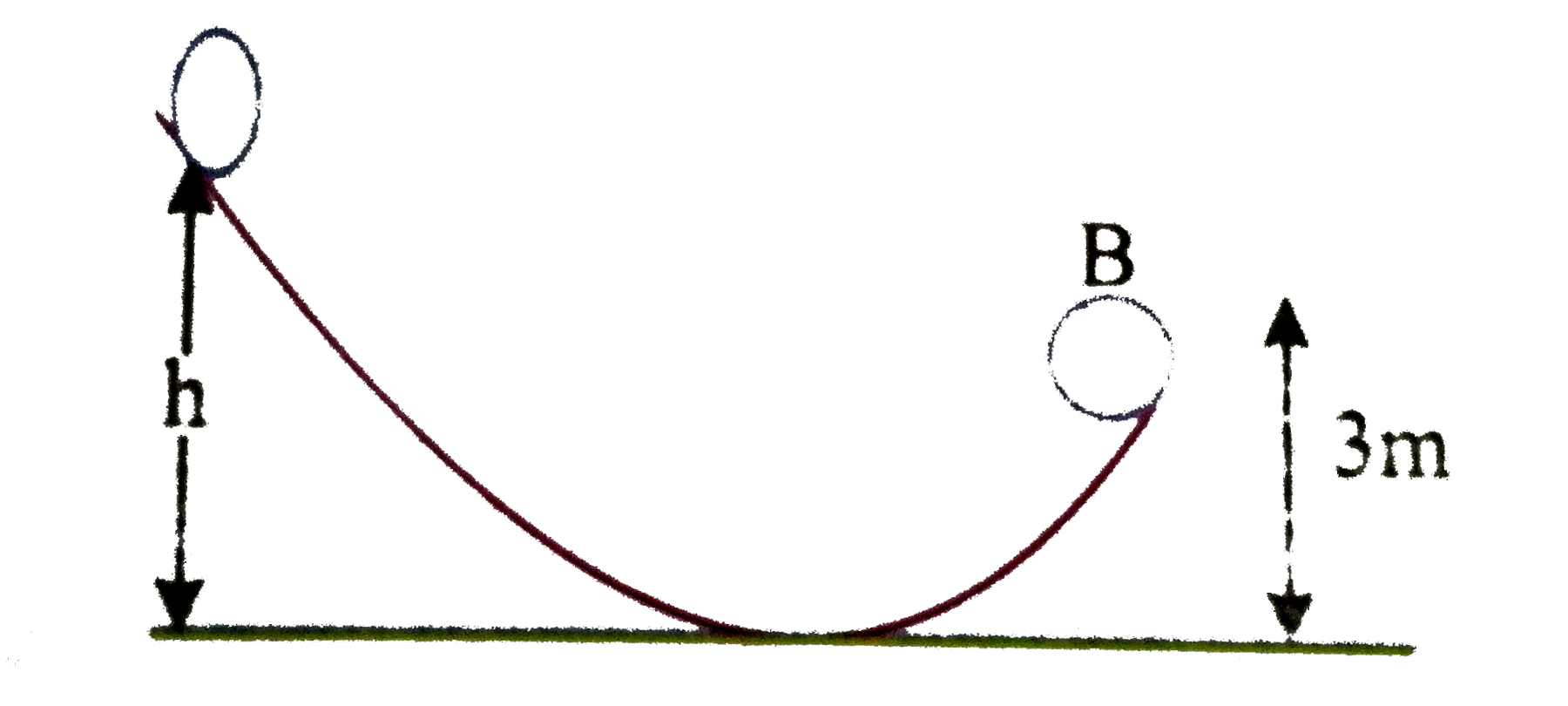
View SolutionA ball leaves the track at B which is at 3m height from bottom most point of the track. The ball further rises upto 4m height from the bottom most point before falling down. Find h (in m), if the track at B makes an angle 30∘ with horizontal.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
As shown in figure, the hinges A and B hold a uniform 400N door in place. The upper hinge supports the entire weight of the door. Find the resultant force exerted on the door at the hinges, the width of the door is h2, where h is the distance between the hinges.
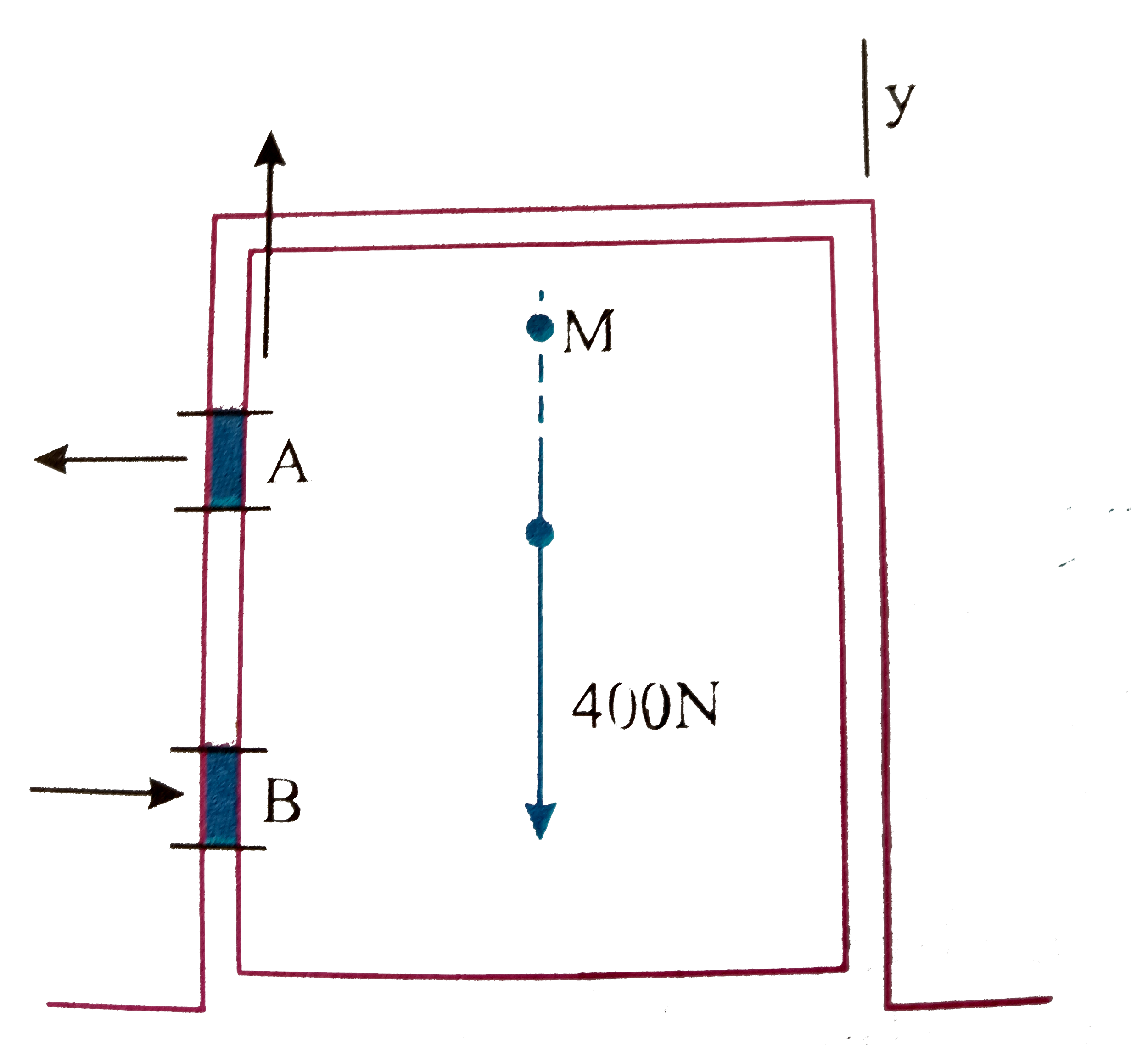 A312NB280NC412ND480N
A312NB280NC412ND480N - Question 2 - Select One
The figure shows the top view of a door that is 2 m wide. Two forces are applied to the door as indicated. What is the magnitude of the net torque on the door with respect to the hinge?
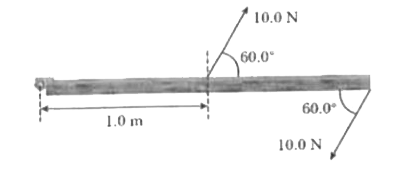 A0N⋅mB10.0N⋅mC5.0N⋅mD8.7N⋅m
A0N⋅mB10.0N⋅mC5.0N⋅mD8.7N⋅m - Question 3 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?View SolutionA uniform rod of mass M=2kg and length L is suspended by two smooth hinges 1 and 2 as shown in Fig. A force F=4N is applied downward at a distance L/4 from hinge 2. Due to the application of force F, hinge 2 breaks. At this instant, applied force F is also removed. The rod starts to rotate downward about hinge 1. (g=10m/s2)

The reaction at hinge 1, before hinge 2 breaks, isView SolutionA uniform rod of mass M=2kg and length L is suspended by two smooth hinges 1 and 2 as shown in Fig. A force F=4N is applied downward at a distance L/4 from hinge 2. Due to the application of force F, hinge 2 breaks. At this instant, applied force F is also removed. The rod starts to rotate downward about hinge 1. (g=10m/s2)

The reaction at hinge 1, just after breaking of hinge 2, isView SolutionA long rod ABC of mass "m" and length "L" has two particles of masses "m" and "2m" attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with A hinged at the bottom is
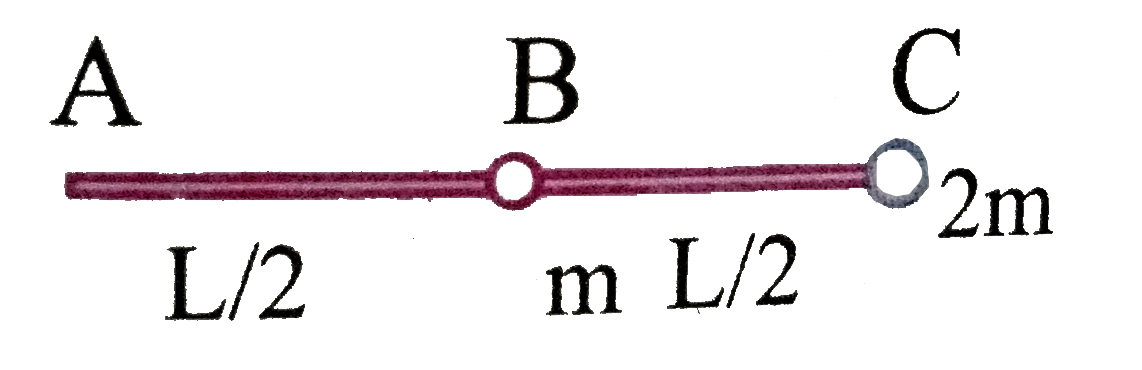 .View Solution
.View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
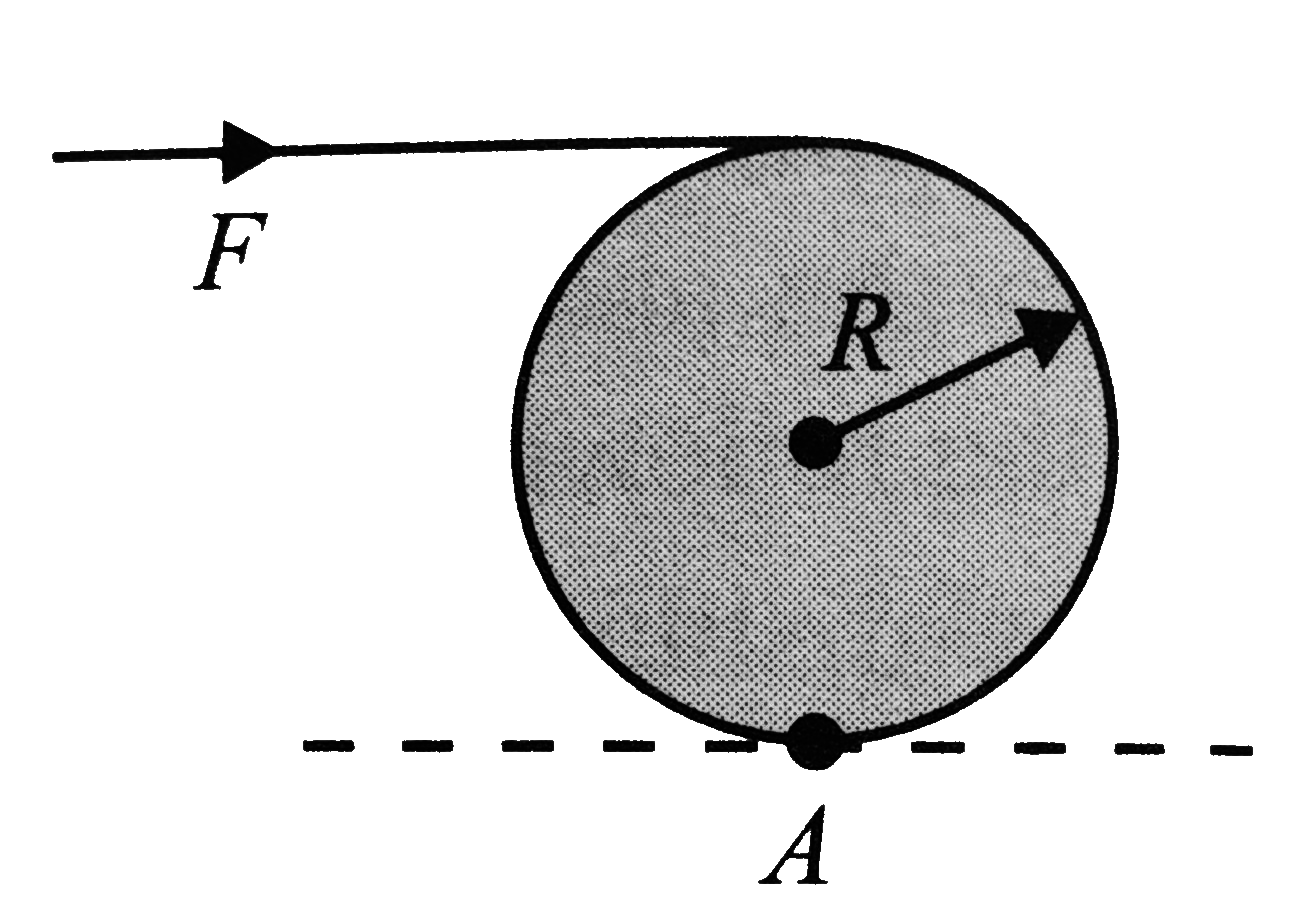
Component of reaction at the hinge in the horizontal direction isView Solution

