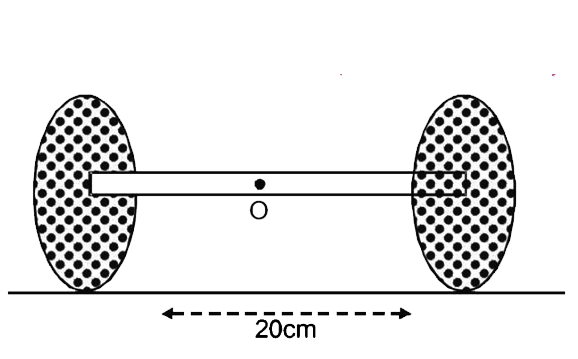
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors in the x,y, and z directions.
The correct Answer is:
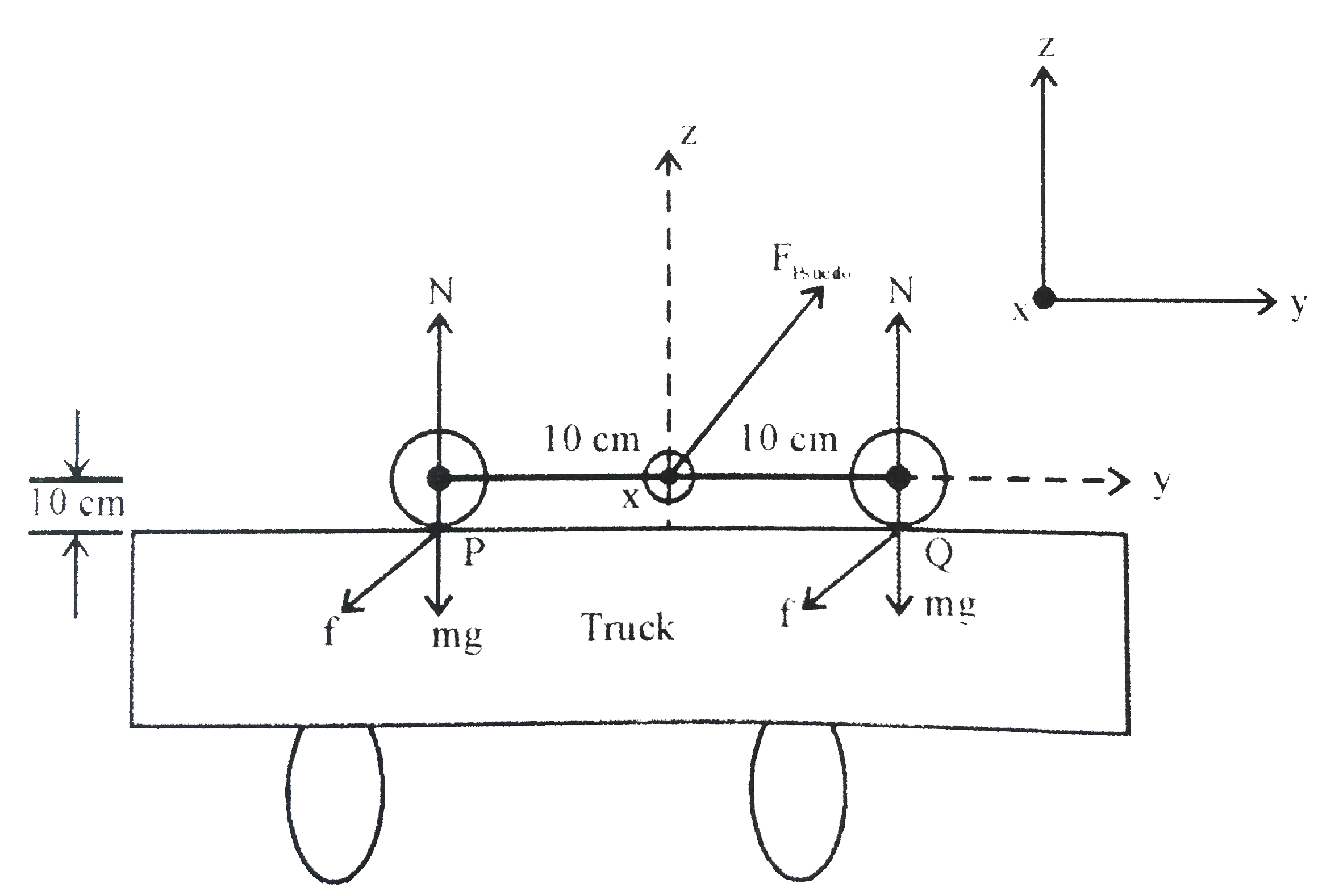
For translation motion
…(1)
For rotational motion
...(2)
From (1) and (2)
.
Similar Questions
The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about axis perpendicular to the rod through its end point is
View SolutionThe M.I. of a thin rod of length 1 about the perpendicular axis through its centre is I. The M.I. of square structure made by four such rods a perpendicular axis to the plane and through the centre will be:
View Solutionद्रव्यमान M व लम्बाई L की पतली छड़ की घूर्णन त्रिज्या छड़ की लम्बाई के लम्बवत् तथा छड़ के एक सिरे से गुजरने वाले अक्ष के परितः ज्ञात कीजिये।
View Solutionएक पतली वृत्ताकार चकती का द्रव्यमान 2kg एवं व्यास 0.2m है। चकती का जड़त्व आघूर्ण, इसके तल के लम्बवत् एवं किनारे से गुजरने वाली अक्ष के परितः होगा (kg−m2 में)
View Solution1kg द्रव्यमान तथा 2m त्रिज्या की वृत्तीय चकती के तल के लम्बवत्, द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण 2kgm2 है। चकती के सतह से गुजरने वाले अक्ष के समानान्तर जड़त्व आघूर्ण होगा (दिये गये चित्रानुसार)
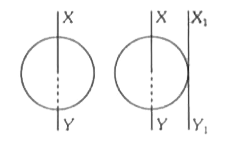
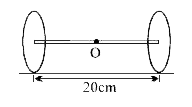
View Solution2kg द्रव्यमान तथा 10cm त्रिज्या की दो पतली वृत्ताकार चकतीयों 20cm लम्बाई की एक दृढ़ द्रव्यमानहीन छड़ द्वारा जुड़ी हुई है। छड़ का अक्ष चकतियों के केन्द्र के तलों के लम्बवत् है। वस्तु एक ट्रक पर इस प्रकार रखी हुई कि वस्तु का अक्ष क्षैतिज है तथा ट्रक की गति की दिशा के लम्बवत् है। यदि घर्षण ट्रक के फर्श के साथ बहुत अधिक है ताकि वस्तु बिना फिसले ट्रक पर लुढ़क सके। ट्रक की गति दिशा को x-अक्ष व उर्ध्वाधर ऊपर की दिशा को z-अक्ष के रूप में मानिए। यदि ट्रक का त्वरण 9m/s2 है, तो गणना कीजिए-
(a) प्रत्येक चकती पर घर्षण बल
(b) प्रत्येक चकती पर कार्यरत घर्षण बलाघूर्ण का परिमाण व दिशा वस्तु के द्रव्यमान केन्द्र O के परिता है। x-y व z दिशाओं में एकांक सदिशों के सदिश रूप में बलघूर्ण की व्याख्या कीजिए।
View SolutionFind the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m//s^2 Calculate: (i) The force fo friction on each disk, (ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors hati, hatj and hatk in the x,y, and z directions.
View Solution
