An endless cord consists of lengths 2l and and their masses per unit length are m and . It is placed in stable equilibrium over a smooth peg as shown in the figure. It is slightly displaced and left to itself. Show that motion is simple harmonic. Find the period of oscilattions.

The correct Answer is:
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:NN GHOSHChapter:SIMPLE HARMONIC MOTIONExercise:Eexercies
Explore 39 Videos
- SIMPLE AND COMPOUND PENDULUMBook:NN GHOSHChapter:SIMPLE AND COMPOUND PENDULUMExercise:Exercise
Explore 24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBook:NN GHOSHChapter:SPECIFIC HEAT CAPACITY OF GASESExercise:All Questions
Explore 17 Videos
Similar Questions
A system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
View Solution
Knowledge Check
A system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:
 A2π√√2l3gB2π√2√2l3gC2π√2l3gD3π√l3g
A2π√√2l3gB2π√2√2l3gC2π√2l3gD3π√l3gA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
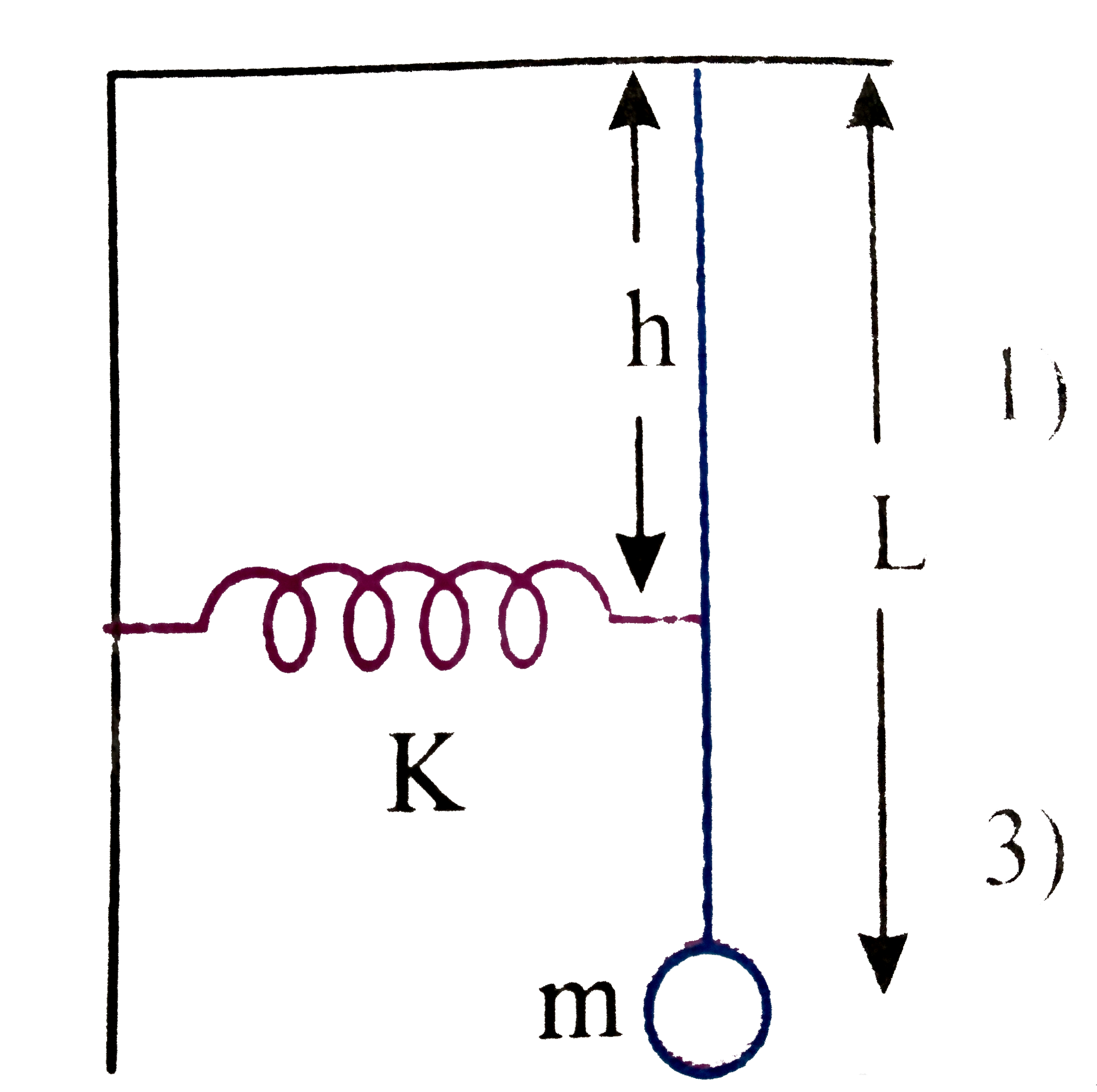 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.A(√2−1)mgB(√2+1)mgC(√3+1)mgD(√2+3)mg
A ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
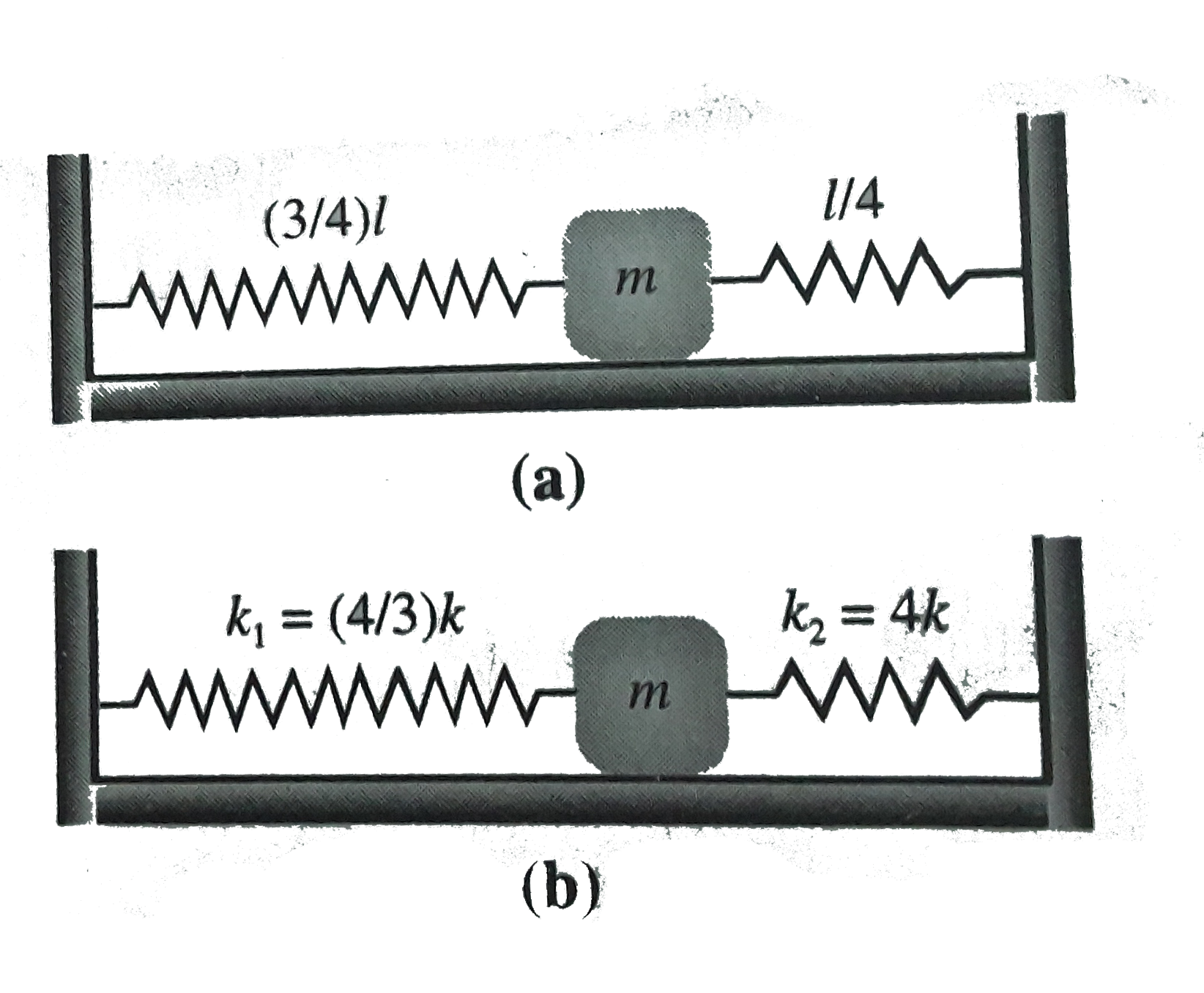
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.

View Solution
