A circle disc has a tiny hole in it, at a distance z from its center. Its mass is M and radius E(R>z). A horizontal shaft is passed through the hole and held fixed so that the disc can freely swing in the vertical plane. For small distrubance, the disc performs SHM whose time period is minimum for z=
R/2
R/3
R/√2
R/√3
The correct Answer is:C
Step by step video, text & image solution for A circle disc has a tiny hole in it, at a distance z from its center. Its mass is M and radius E(Rgtz). A horizontal shaft is passed through the hole and held fixed so that the disc can freely swing in the vertical plane. For small distrubance, the disc performs SHM whose time period is minimum for z= by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
In the figure shwon there is non-conducting disc of mass M=2k and radius R=4m. On its upper & lower part of circumference +Q and −Q charge are uniformly attached such that liner charge density is QπR. The disc can freely rotate about an horizontal axis passing through O. There is a uniform electric field ¯¯¯E in the vertical direction such that QE=mg. If the disc is rotated by a small angle it performs S.H.M. its time period is given by T=≈√πn then, P+n, is (Take π2=g)

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View Solution
Knowledge Check
A small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
AMR29B516MR2C916MR2D54MR2A uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
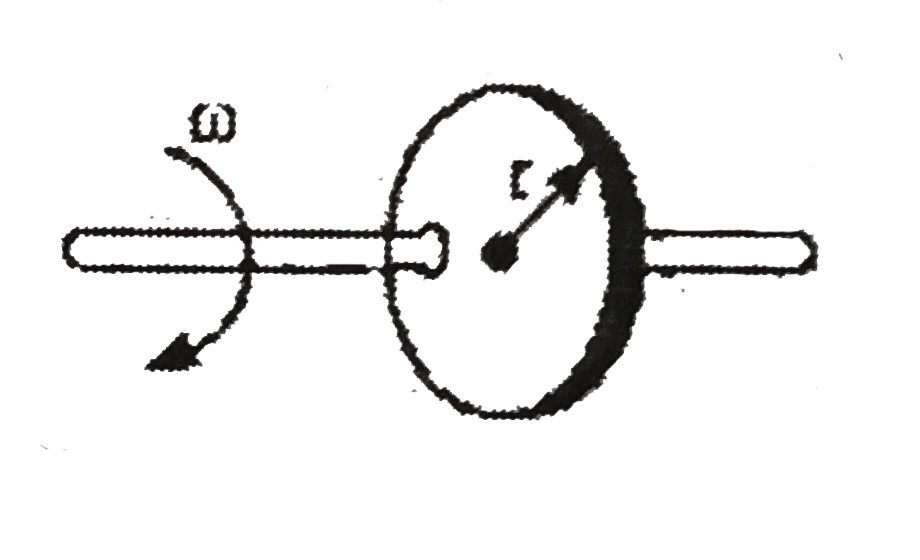 AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zero
AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zeroA uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)
A uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
View SolutionA uniform disc of radius R and mass M can rotate on a smooth axis passing through its centre and perpendicular to its plane. A force F is applied on its rim. See fig. What is the tangential acceleration
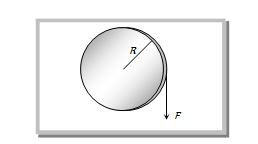
View SolutionA disc is hinged such that it can freely rotate in a vertical plane about a point on its radius. If radius of disc is 'R' , then what will be minimum time period of its simple harmonic motion ?
View SolutionA uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis, passing through the centre of the disc. A piece of disc from its rim detaches itself from the disc at the instant when it is, on the same horizontal with the centre of the disc and moving upwards. lien about the fixed axis, the angular speed of the
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View Solution
