A disc is hinged such that it can freely rotate in a vertical plane about a point on its radius. If radius of disc is 'R' , then what will be minimum time period of its simple harmonic motion ?
2π√Rg
2π√3R2g
2π√√2Rg
2π√R2g
The correct Answer is:C
For minimum time period
x=R√2
⇒T=2π
⎷mR22+mR22mgR√2=2π√√2Rg
i=⎡⎢
⎢
⎢⎣M(R√2)212+M(R√2)2⎤⎥
⎥
⎥⎦×4+mR2
=20kgm2.
(4M+m)gsinθ−F=(4M+m)a.
F.R.=I(aR)
Solving
a=7g24
F=20a≤μ(4M+m)gcos30
μ≥512√3
∴μmin=512√3

Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 765videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 778videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 747videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A uniform circular disc of radius R oscillates in a vertical plane about a horizontal axis. Find the distance of the axis of rotation from the centre of which the period is minimum. What is the value of this period?
View SolutionA disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A brass disc is rotating about its axis. If temperature of disc is increased then its
Aradius of gyration increases, but moment of inertia remains the sameBmoment of inertia increases but radius of gyration remains the sameCradius of gyration, moment of inertia both remain the sameDradius of gyration, moment of inertia both increase - Question 2 - Select One
A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant isAMg5(R2+2r2)×√9(R2+6r2)2+(4R2)2BMg5(R2+2r2)×3(R2+6r2)C4Mg5(R2+2r2)×R2DMg5(R2+2r2)×4R2 - Question 3 - Select One
A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
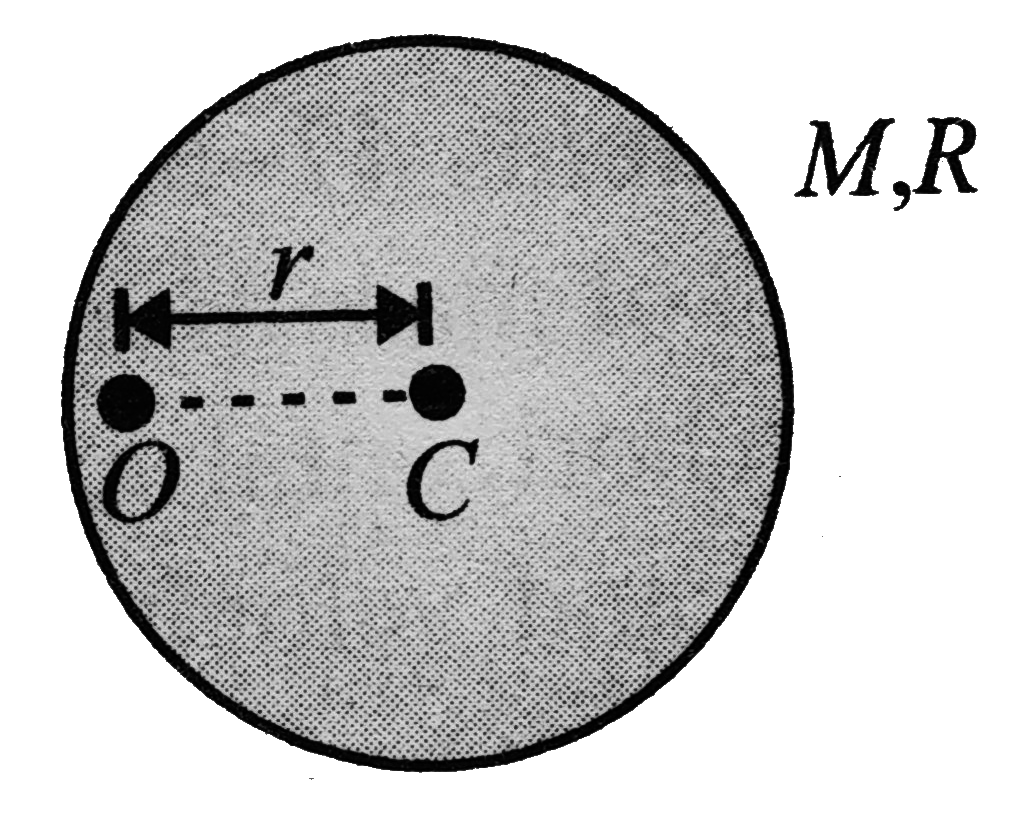
The angular velocity of the disc in the above described case isA√8gr5{R2+2r2]B√6gr5[R2+2r2]C√12gr5[R2+2r2]D√12gr5R2
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the centre of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ isView SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. The time period of small oscillations of remaining portion about O is -
 View Solution
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
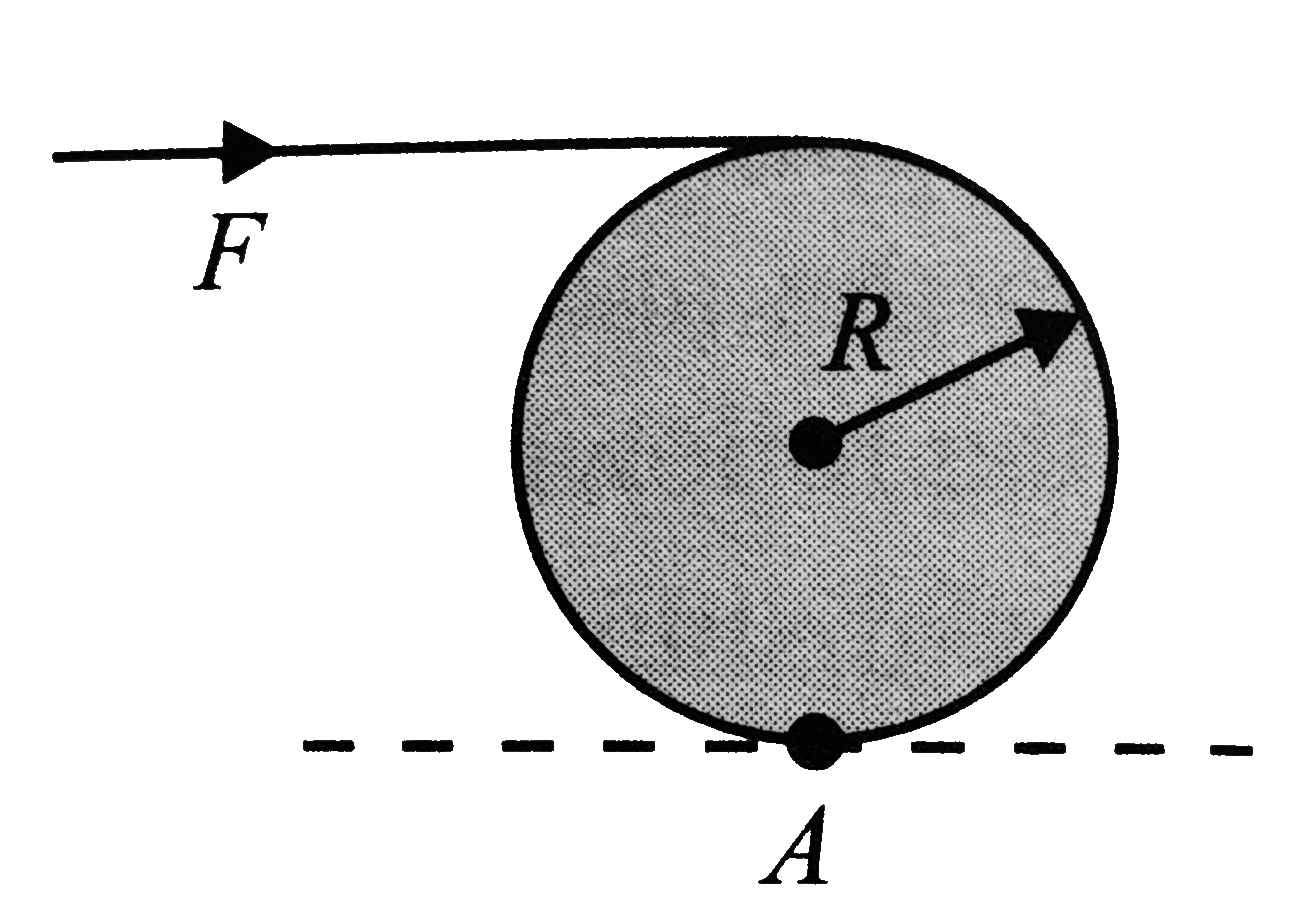
Component of reaction at the hinge in the horizontal direction isView SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
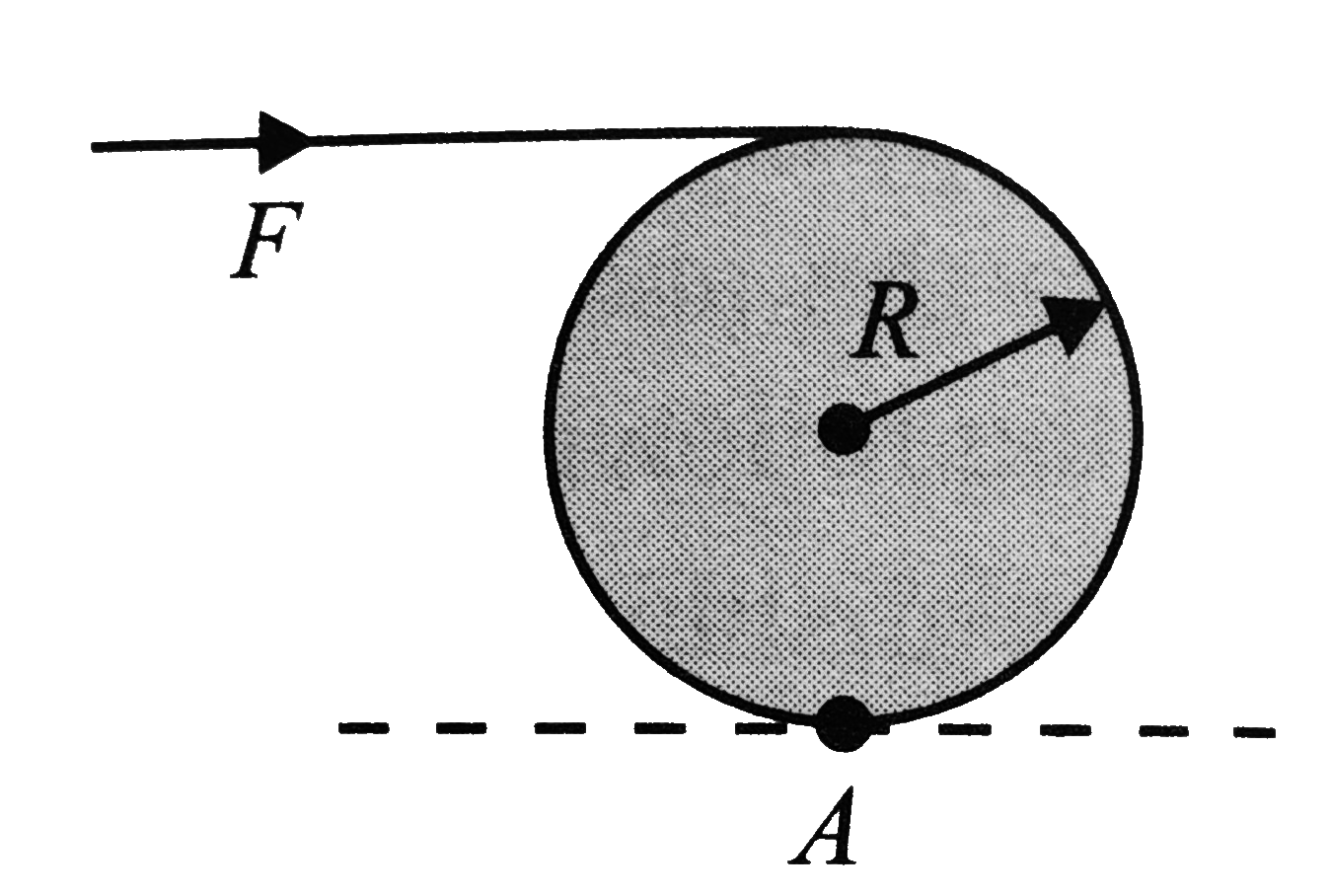
Tangential acceleration of the centre of mass isView Solution

