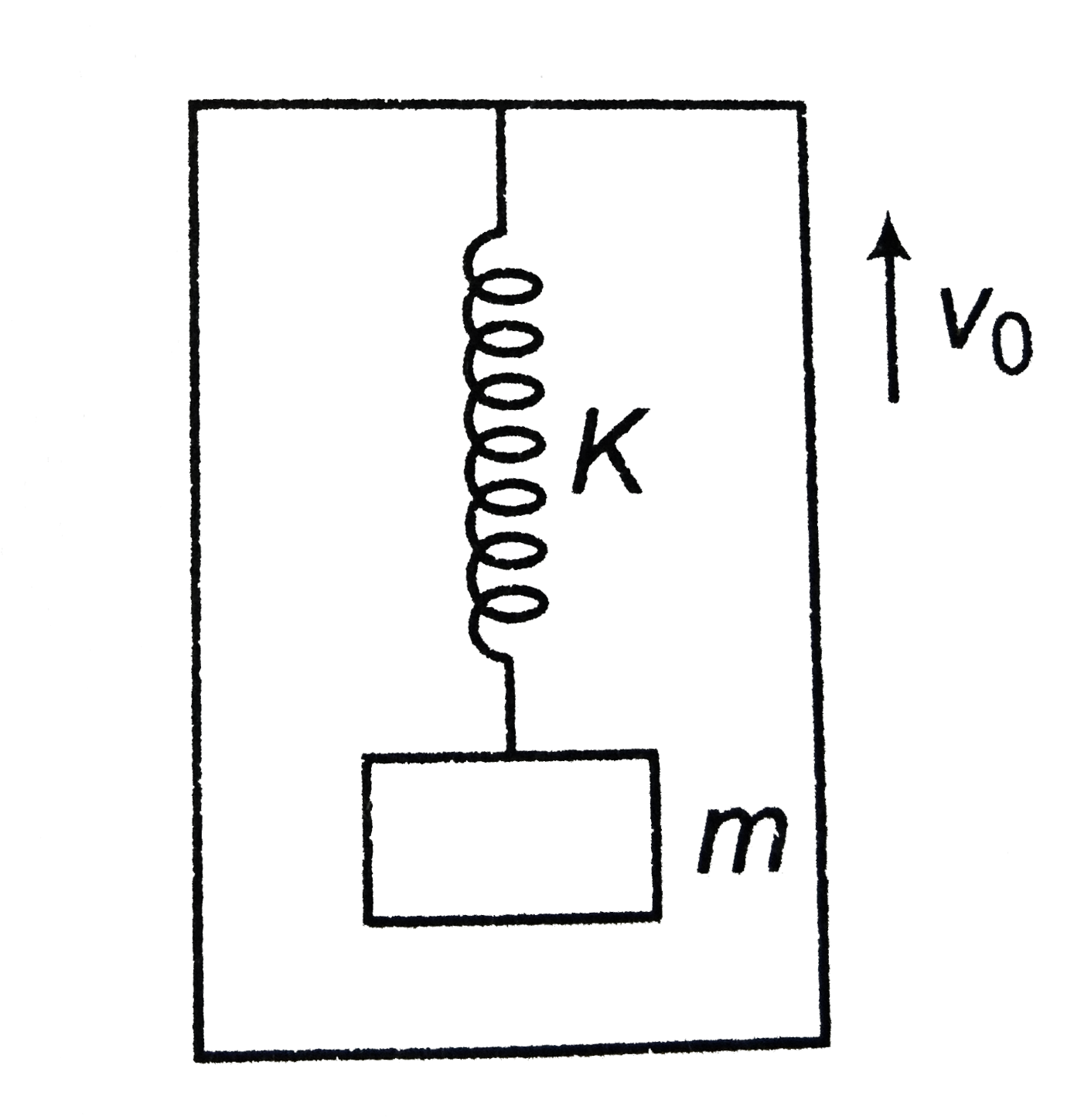
The angular frequency of a spring block system is ω0. This system is suspended from the ceiling of an elevator moving downwards with a constant speed V0. Ther block is at rest relative to the elevator. Lift is suddenly stopped. Assuming the downwards as a positive direction, choose the wrong statement:
The amplitude of the block is v0ω0
The initial phase of the block is π.
The equation of motion for the block is v0ω0sinω0t.
The maximum speed of the block is v0.
The correct Answer is:B
Figure
Similar Questions
The angular frequency of a spring block system is ω0. This system is suspended from the ceiling of an elevator moving downwards with a constant speed v0. The block is at rest relative to the elevator. Lift is suddenly stopped. Assuming the downward as a positive direction. Then
View SolutionA spring block system is kept inside a lift moving with a constant velocity v0 as shown in figure. Block is in equilibrium and at rest with respect to lift. The lift is suddenly stopped at time t=0. Taking upward direction as the positive direction, write x−t equation of the block.
View Solution
Knowledge Check
The angular frequency of a spring block system is ω0. This system is suspended from the ceiling of an elevator moving downwards with a constant speed v0. The block is at rest relative to the elevator. Lift is suddenly stopped. Assuming the downward as a positive direction. Then
AThe amplitude of the block is v0ω0BThe equation of motion for the block is (v0ω0)sinω0tCBoth are correctDBoth are wrongThe angular frequency of a spring block system is ω0. This system is suspeded from the ceilling of an elevator moving downwards with a constant speed v0. The block is at reast realtive to the elevator. Lift is suddenly stopped. Assuming the downward as a positive direction, choose the wrong statement :
Athe amplitude of the block is v0ω0Bthe initial phase of the block is πCthe equation of motion for the block is v0ω0sinω0tDthe maximum speed of the block is v0A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is
Aless than two secondsBequal to two secondsCgreater than two secondsDvery much greater than two seconds
A spring block system is kept inside a lift moving with a constant velocity v0 as shown in figure. Block is in equilibrium and at rest with respect to lift. The lift is suddenly stoped at time t=0. Taking upward direction as the positive direction, write x−t equation of the block.
View SolutionA particle that hangs from a spring oscillates with an angular frequency of 2rad/s. The spring particle system is suspended from the celling of an elevator car and hangs motionless (relative to the elevator car) as the car descends at a constant speed of 1.5m/s. The car then stops suddenly. (a) With what amplitude does the particle oscillate ? (b) What is the equation of motion for the particle ? (Choose upward as the position direction)
View SolutionA particle that hangs from a spring oscillates with an angular frequency of 2rad/s. The spring particle system is suspended from the celling of an elevator car and hangs motionless (relative to the elevator car) as the car descends at a constant speed of 1.5m/s. The car then stops suddenly. (a) With what amplitude does the particle oscillate ? (b) What is the equation of motion for the particle ? (Choose upward as the position diriction)
View SolutionA spring mass system is hanging from the ceiling of an elevator in equilbrium Elongation of spring is l. The elevator suddenly starts accelerating downwards with acceleration g/3 find.
(a) the frequency and
(b) the amplitude of the resulting SHM

View SolutionA spring block (force constant k=1000N/m and mass m=4kg) system is suspended from the ceiling of an elevator such that block is initially at rest. The elevator begains to move upwards at t=0. Acceleration tome graph of the elevator is shown in the figure. Draw the displacement X (from its initial position taking upwards as positive) vs time graph of the block with respect to the elevator starting from t=0 to t=1sec. Take π2=10.

View Solution
