Block A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
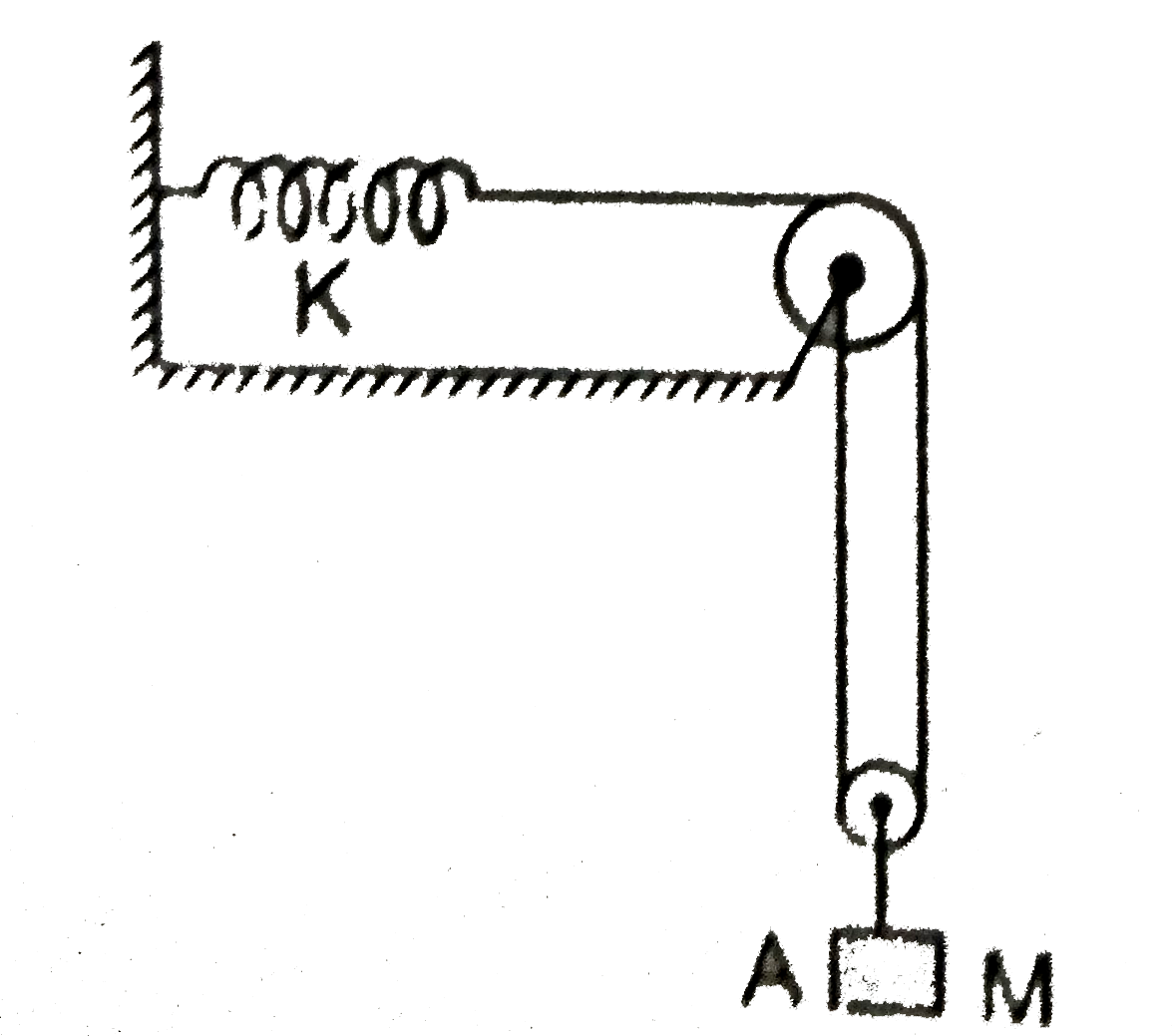
Mg/2k−x0
Mg/2k+x0
2Mg/k−x0
2Mg/k+x0
The correct Answer is:A
From work, energy theorem :
Wg+Ui0Uf=ΔK
Mgh+12K(x20−(x0+2h)2)=−Mgh
⇒12K(x0+x0+2h)(x0−x0−2h)=−Mgh
⇒12K2(x0+h)(−2h)=−Mgh
h=Mg2K−x0.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 417videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 427videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 393videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A body is given a velocity √2gr at the highest point of a half circular smooth track which is joined by a rough horizontal track whose co− efficient of friction is μ=0.5. Then the distance travelled by particle before it stops on horizontal track is :(r=1m)
 02:10View Solution
02:10View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 04:05View Solution
04:05View SolutionTwo objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time t=0. The distance moved by the object when one overtakes the
03:29View SolutionSpecific resistance of a wire depends on its
View SolutionA wire loaded by a weight of density 7.6gcm−3 is found to measure 90cm. On immersing the weight in water, the length decreases by 0.18cm. Find the original length of wire.
02:41View SolutionBlock A of the mass M in the figure is released from rest when the extension in the spring is x0. The maximum downwards displacement of the block is (assume x0<Mg/k).
 02:40View Solution
02:40View SolutionThe given arrangement is released from rest when spring is in natural length. Maximum extension in spring during the motion is x_(0). a_(1),a_(2) and a_(3) are accelerations of the blocks. Make the correct options
11:59View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :
 02:08View Solution
02:08View SolutionIn above question, speed of block A, when the extension in spring is xm2, is:
02:44View SolutionA block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
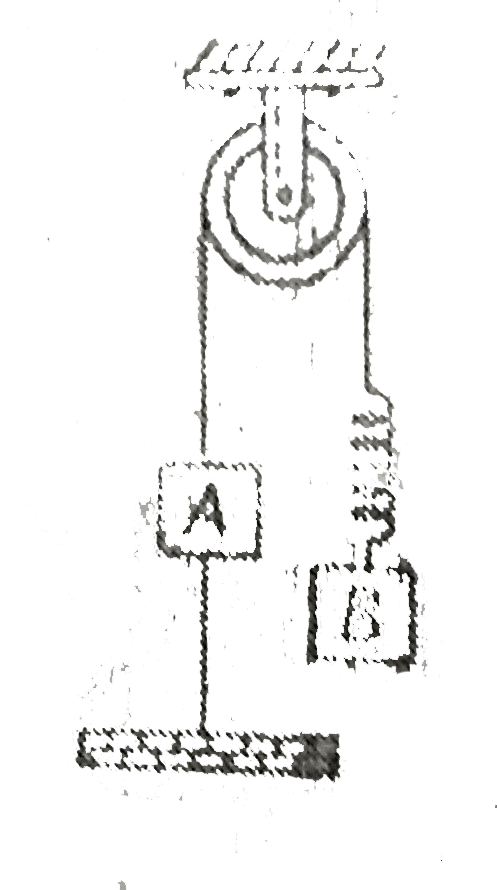 04:34View Solution
04:34View SolutionConsider the situation shown in figure. Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find (a) The maximum extension of the spring x_(m) (b) The speed of block A when the extension in the springt is x=(x_(m))/(2) (c ) The net acceleration of block B when extension in the spring is x=(x_(m))/(4).
02:18View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 02:42View Solution
02:42View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
03:17View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.
 07:57View Solution
07:57View Solution

