(a) Find the time period of oscillations of a torsinal pendulum, if the torsional, constant of the wire is K=10π2J/rad. The moment of inertia of rigid body is 10kgm2 about the axis of rotation.
(b) A simple pendulum of length l=0.5m is hanging from ceiling of a car. the car is kept on a horizontal plane. The car starts acceleration of 5m/s2. find the time period of oscillations of the pendulum for small amplitudes about the mean position.
The correct Answer is:(a) 2sec., (b) T=251/4sec
Step by step video, text & image solution for (a) Find the time period of oscillations of a torsinal pendulum, if the torsional, constant of the wire is K=10pi^(2)J//rad. The moment of inertia of rigid body is 10 kg m^(2) about the axis of rotation. (b) A simple pendulum of length l=0.5 m is hanging from ceiling of a car. the car is kept on a horizontal plane. The car starts acceleration of 5m//s^(2). find the time period of oscillations of the pendulum for small amplitudes about the mean position. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionA simple pendulum of length l and mass m is suspended in a car that is moving with constant speed v around a circle of radius r. Find the period of oscillation and equilibrium position of the pendulum.
View Solution
Knowledge Check
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
A1.90sB1.70sC2.30sD1.40sA simple · pendulum of length L is hanging from a rigid support on the ceiling of a stationary train. If the train moves forward with an acceleration a, then the time period of the pendulwn will be
A2π√L(g2+a2)1/2B2π√L(g2−a2)1/2C2π√L(g+a)D2π√L(g−a)A simple pendulum of length l is made to oscillate with an amplitude of 45 degrees. The acceleration due to gravity is g. Let T0=2π√l/g . The time period of oscillation of this pendulum will be -
AT0 irrespective of the amplitudeBslightly less than T0Cslightly more than T0Ddependent on whether it swings in a plane aligned with the north-south or east-west directions
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
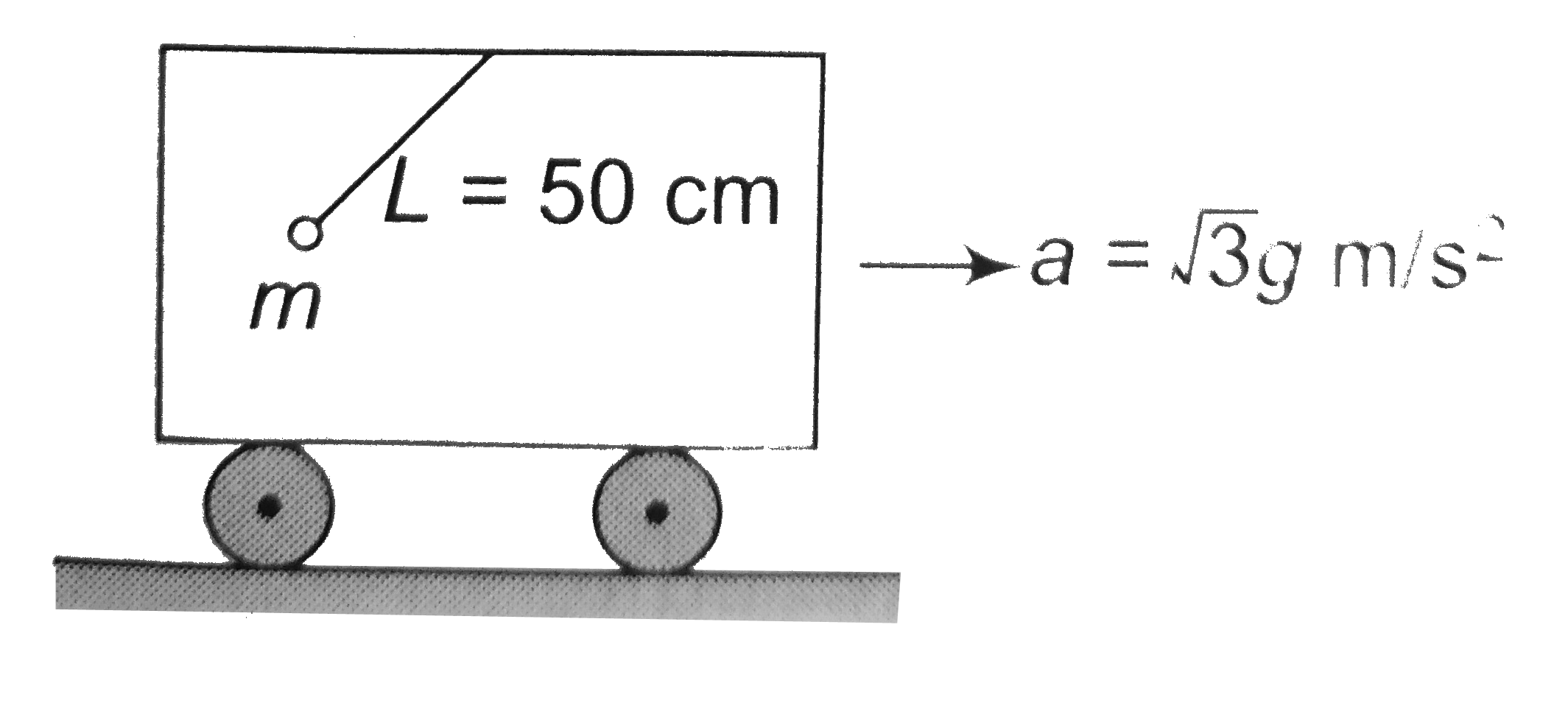
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
View SolutionThere is a simple pendulum hanging from the ceiling of a lift. When the lift is stand still, the time period of the pendulum is T . If the resultant acceleration becomes g/4 ,then the new time period of the pendulum is
View SolutionThe acceleration due to gravity at a place is π2m/s2. Then, the time period of a simple pendulum of length 1 m is
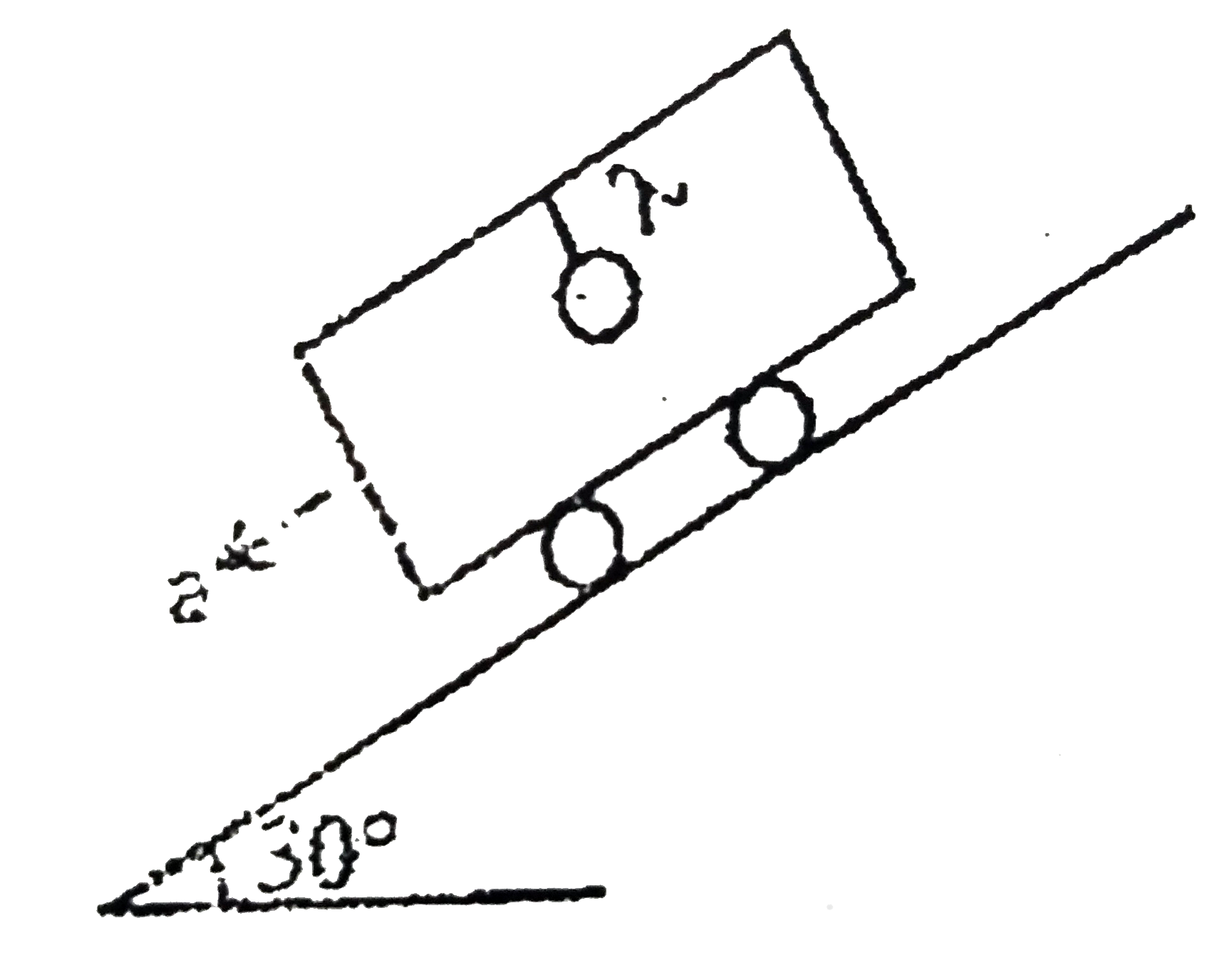
View SolutionA car is acclerating down on an inclined plane as shown in the figure with acceleration a=g. Now find time period of SHM of the pendulum present inside the car.
View Solution
