The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.

If x=2R,then the value of μis
1.5
2
3
none of these
The correct Answer is:C
μ2v−μ1u=μ2−μ1R⇒μ2R−1−2R=μ−12R
μ2R=μ−1R−12R⇒μ2R=2μ−2−12R
μ=2μ−3
μ=3
Similar Questions
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
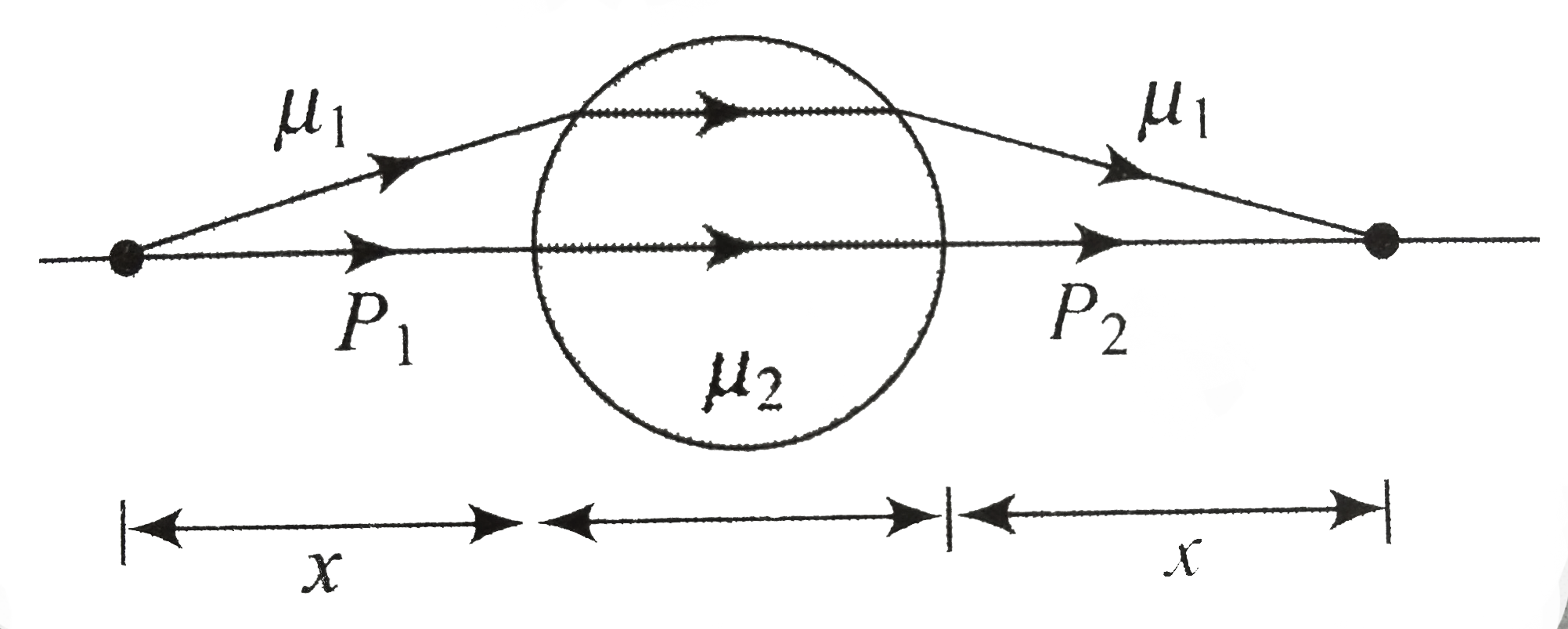 View Solution
View SolutionA transparent sphere of radius R and refractie index μ is kept in air. At what distance from the surface of the sphere shold a point object be placed so as to form a rea image at the same distance from the sphere?
View Solution
Knowledge Check
- Question 1 - Select One
The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
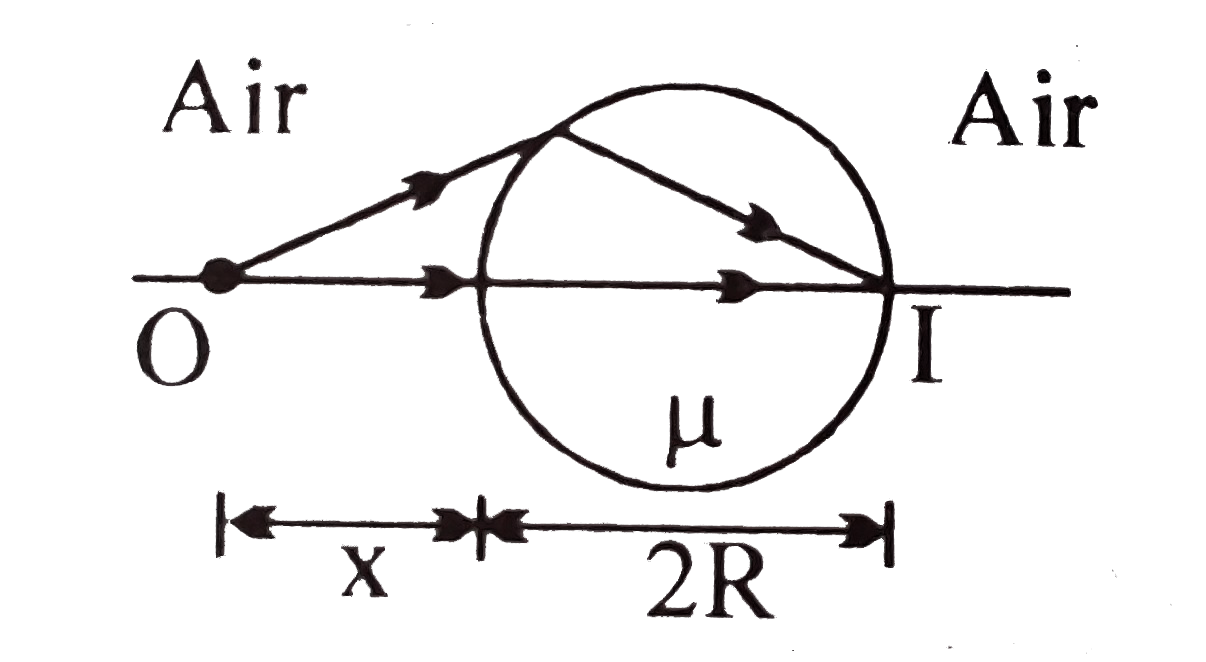 If x=∞,then the value of μ isA1.5B2C3DNone of these
If x=∞,then the value of μ isA1.5B2C3DNone of these - Question 2 - Select One
The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of these
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of these - Question 3 - Select One
There is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
ARμ−1BRμCR2−μD2Rμ−1
A hemishperical surface of radius R and refractive index μ=1.5 is polished as shown. At what distance x from point P a point object O be placed so that its image coincides with the object itself?
 View Solution
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:
 View Solution
View SolutionA point object is placed in air at a distance of 40 cm from a concave refracting surface of refractive index 1.5. If the radius of curvature of the surface is 20 cm, then the position of the image is –
View SolutionAn object is placed in front of a sphere of radius R at a distance x from the first surface. The value of x for which the light after refraction from the first surface becomes parallel to the axis is
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View Solution

