Calculate the electric potential at the center of a square of side √2m, having charges 100μc,−50μC,20μcand−60μC at the four corners of the square.
To calculate the electric potential at the center of a square with charges at its corners, we will follow these steps:
Step 1: Identify the charges and their positions
We have four charges located at the corners of a square:
- Charge at A: Q1=100μC=100×10−6C
- Charge at B: Q2=−50μC=−50×10−6C
- Charge at C: Q3=20μC=20×10−6C
- Charge at D: Q4=−60μC=−60×10−6C
Step 2: Calculate the distance from the center to each charge
The side of the square is given as √2m. The distance from the center of the square to any corner can be found using the diagonal:
- The diagonal AC of the square can be calculated using the Pythagorean theorem:
AC=√(√2)2+(√2)2=√2+2=√4=2m
- The distance R from the center to each charge is half of the diagonal:
R=AC2=22=1m
Step 3: Use the formula for electric potential
The electric potential V due to a point charge is given by:
V=14πϵ0QR
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
Step 4: Calculate the total electric potential at the center
The total electric potential Vtotal at the center due to all four charges is:
Vtotal=V1+V2+V3+V4
Substituting the values:
Vtotal=14πϵ0(Q1R+Q2R+Q3R+Q4R)
Since R=1m, we can simplify:
Vtotal=14πϵ0(Q1+Q2+Q3+Q4)
Substituting the charges:
Vtotal=14πϵ0(100×10−6−50×10−6+20×10−6−60×10−6)
Calculating the sum of charges:
=14πϵ0(100−50+20−60)×10−6
=14πϵ0(10×10−6)
Step 5: Calculate the numerical value
Using ϵ0≈8.85×10−12:
Vtotal=14π(8.85×10−12)×10×10−6
Calculating 14π(8.85×10−12)≈9×109:
Vtotal≈9×109×10×10−6
=9×104V=90,000V
Final Answer
The electric potential at the center of the square is approximately 90,000V or 9×104V.
We have four charges located at the corners of a square:
- Charge at A: Q1=100μC=100×10−6C
- Charge at B: Q2=−50μC=−50×10−6C
- Charge at C: Q3=20μC=20×10−6C
- Charge at D: Q4=−60μC=−60×10−6C
The side of the square is given as √2m. The distance from the center of the square to any corner can be found using the diagonal:
- The diagonal AC of the square can be calculated using the Pythagorean theorem:
AC=√(√2)2+(√2)2=√2+2=√4=2m
- The distance R from the center to each charge is half of the diagonal:
R=AC2=22=1m
The electric potential V due to a point charge is given by:
V=14πϵ0QR
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
The total electric potential Vtotal at the center due to all four charges is:
Vtotal=V1+V2+V3+V4
Substituting the values:
Vtotal=14πϵ0(Q1R+Q2R+Q3R+Q4R)
Since R=1m, we can simplify:
Vtotal=14πϵ0(Q1+Q2+Q3+Q4)
Substituting the charges:
Vtotal=14πϵ0(100×10−6−50×10−6+20×10−6−60×10−6)
Calculating the sum of charges:
=14πϵ0(100−50+20−60)×10−6
=14πϵ0(10×10−6)
Using ϵ0≈8.85×10−12:
Vtotal=14π(8.85×10−12)×10×10−6
Calculating 14π(8.85×10−12)≈9×109:
Vtotal≈9×109×10×10−6
=9×104V=90,000V
The electric potential at the center of the square is approximately 90,000V or 9×104V.
Similar Questions
Define the term electric potential due to a point charge .
Calculate the electric potential at the centre of a square , of side √2 m , having charges 100μC,−50μC,20μC and −60μC at the four corners of this square .
View SolutionFind the electric field and potential at the centre of a square of side d = 10 cm. Four identical charges of q=2μC each are kept at the four corners of a square.
View Solution
Knowledge Check
Electric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
A1.8 VB1.8×106VC1.8×105VD1.8×104VA particle carrying charge + q is held at the center of a square of each side arranged on the square as shown in Fig. If q = 2 muC, what is the net force on the particle?
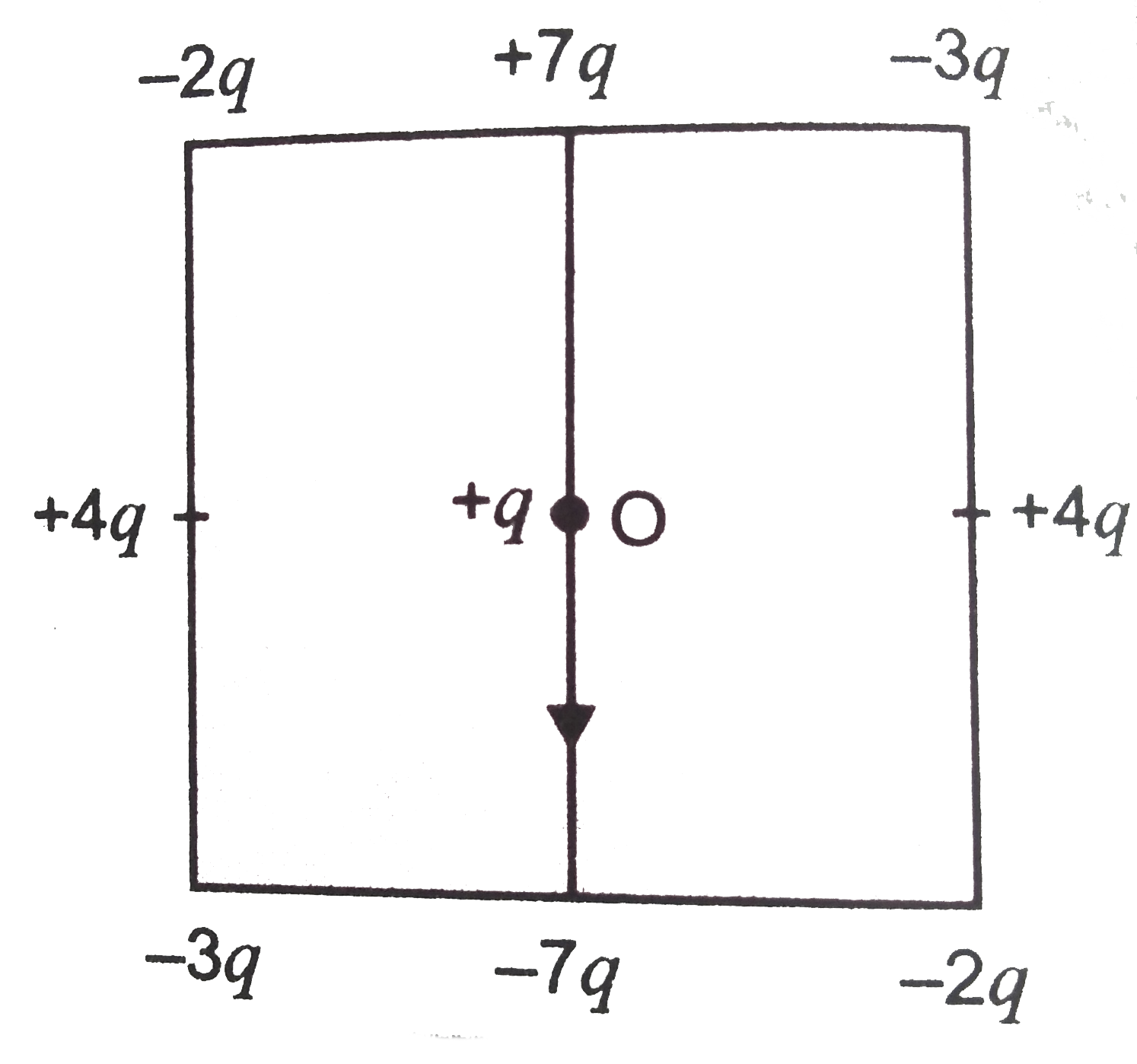 A36×14×4×10−3NB16×14×4×10−3NC26×14×4×10−3ND6×14×4×10−3N
A36×14×4×10−3NB16×14×4×10−3NC26×14×4×10−3ND6×14×4×10−3NA charge of 10μC lies at the centre of a square. Work done in carrying a charge of 2μC from one corner of square to the diagonally opposite corner is
A20JB5JCZeroD20μJ
Calculate the electric potential at the centre of a metallic ring with charge 0.02 μC made from a wire of length 12 cm.
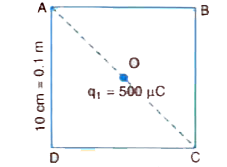
View SolutionA500μC charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10μC between two diagonally opposite points on the square.
View SolutionCalculate the electric field intensity due to an electric dipole of length 10 cm having charges of 100μC at a point 20 cm from each charge on equatorial line.
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View Solution
