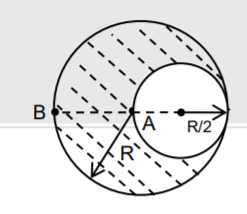
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
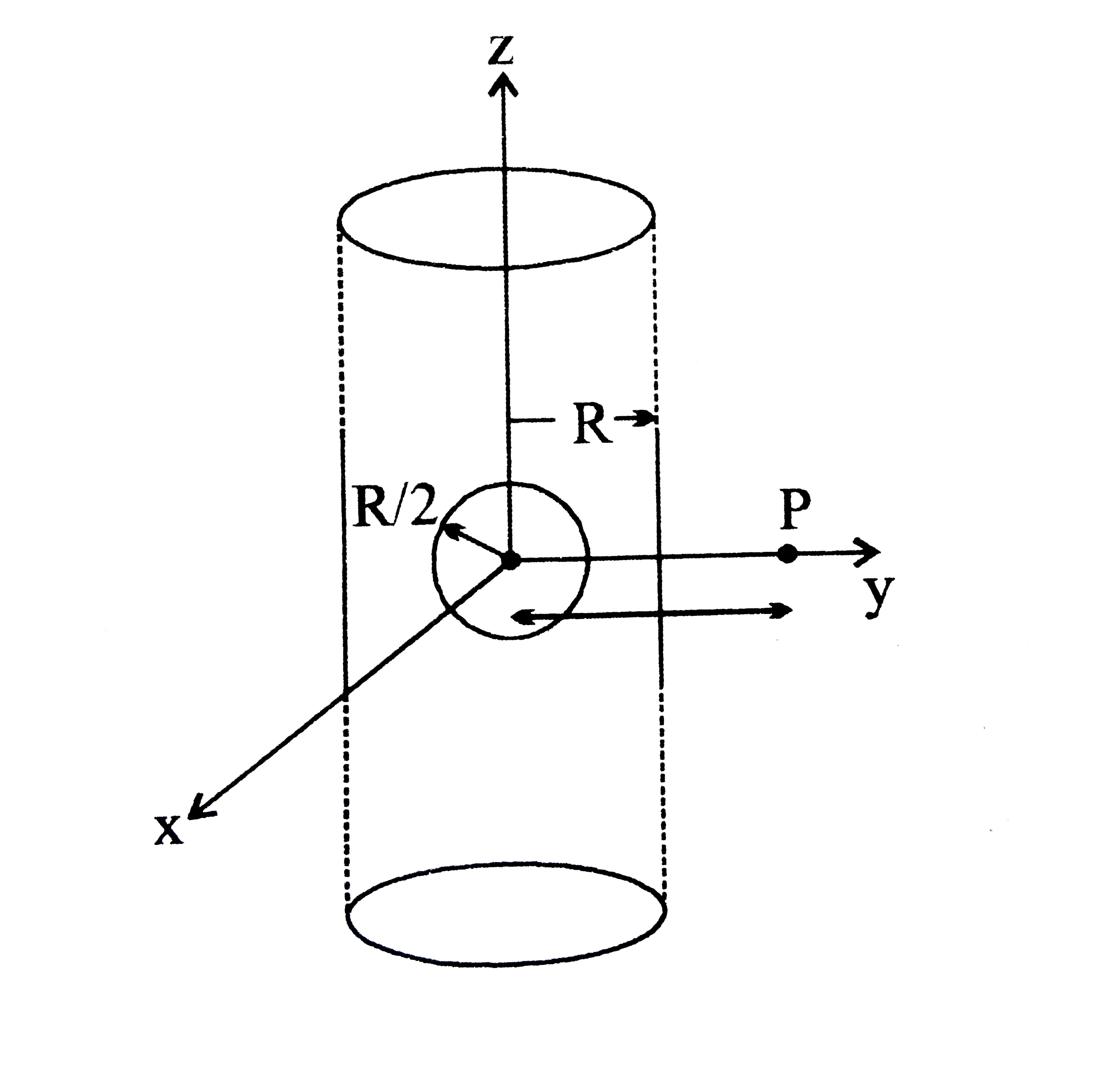 .
.
The correct Answer is:2
Due to symmetry of charge distribution the electric field at a point outside the cylinder is ⊥r to the axis of cyclinder , outwards. Let −→E1 be the electric field intensity at P due to charge on solid cylinder.
Draw a cylinderical gaussain surface of radius 2R and height R as shown in Fig, so that point P lies on the curved surface of gaussain cylindrical.
Electric flux over the gaussain cylindrical surface =∮−→E1.→ds=1∈0× charge enclosed by the surface
∴E1(2π×2R)R=1∈0(πR2)Rρ
=1∈0πR3ρ
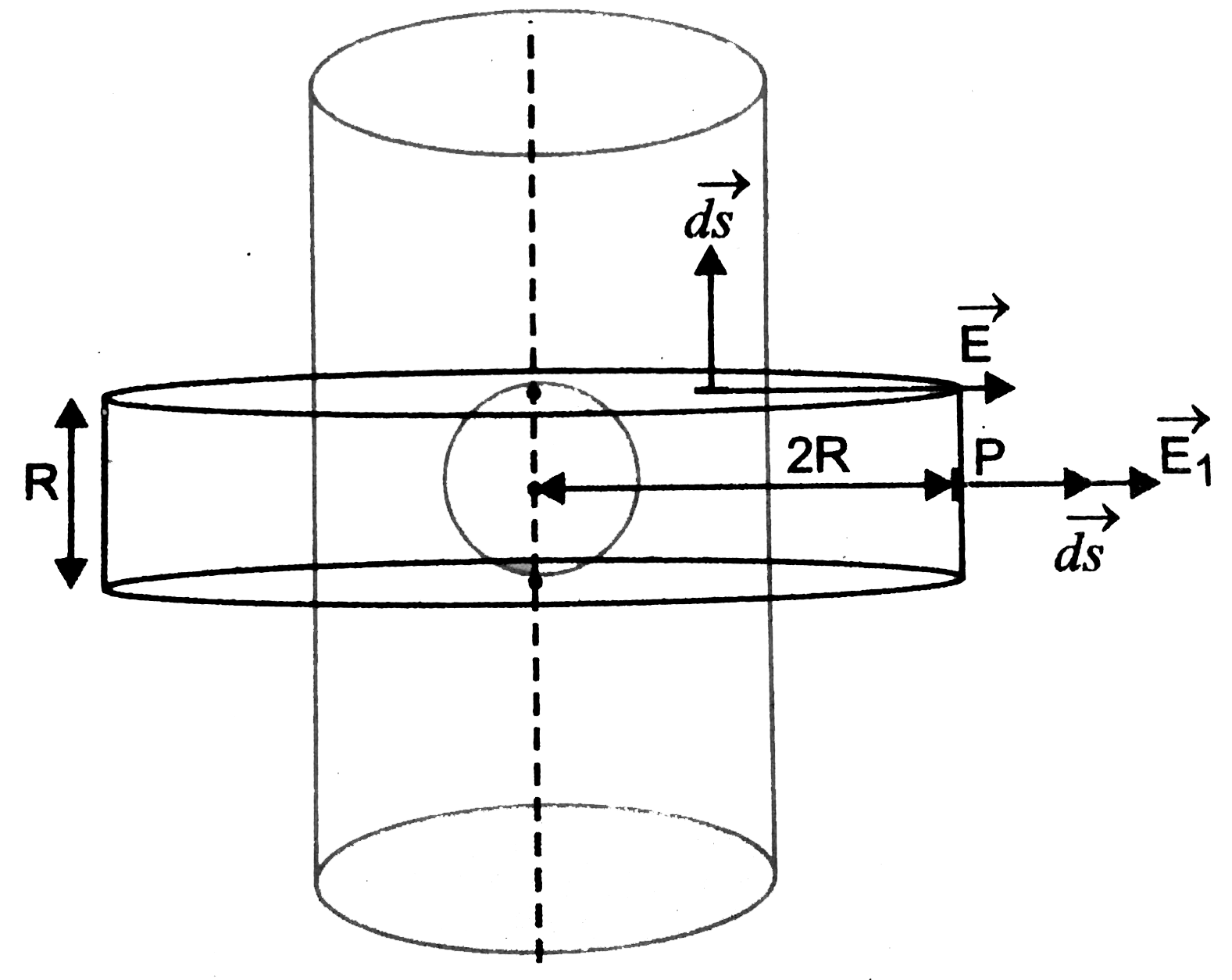
or E1=1∈0πR3ρ4πR2=Rρ4∈0 ..(i)
Charge on cavity of radius R/2,
q=43π(R/2)3ρ=πR3ρ/6
Electric fiedl intensity at P due to charge on spherical cavity is
E2=14π∈0=q(2R)2=14π∈0×πR3ρ/64R2
=Rρ96∈0 ...(i)
Hence net electric field, E=E1−E2
=Rρ4∈0−Rρ96∈0=23ρR96∈0
As per question, =23ρR96∈0=23ρR16k∈0
∴16k=96 or k=6
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
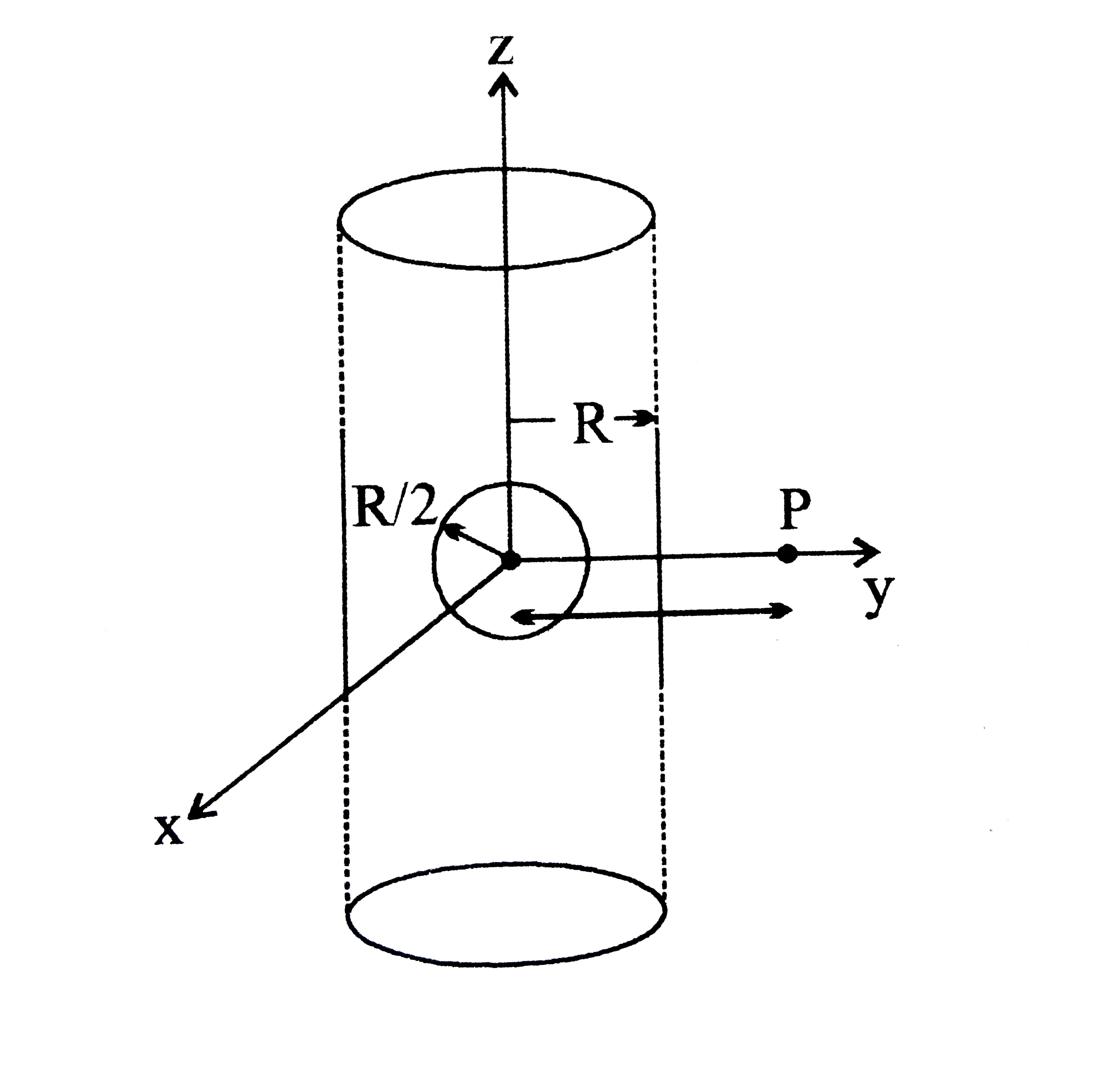 .
.
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R2 with its center on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which at a distance 2 R (from the axis of the cylinder, is given by the expression 23ρR16nɛ0, The value of n is
'(##CEN_KSR_PHY_JEE_C18_E01_040_Q24##)'
View Solution
Knowledge Check
Inside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
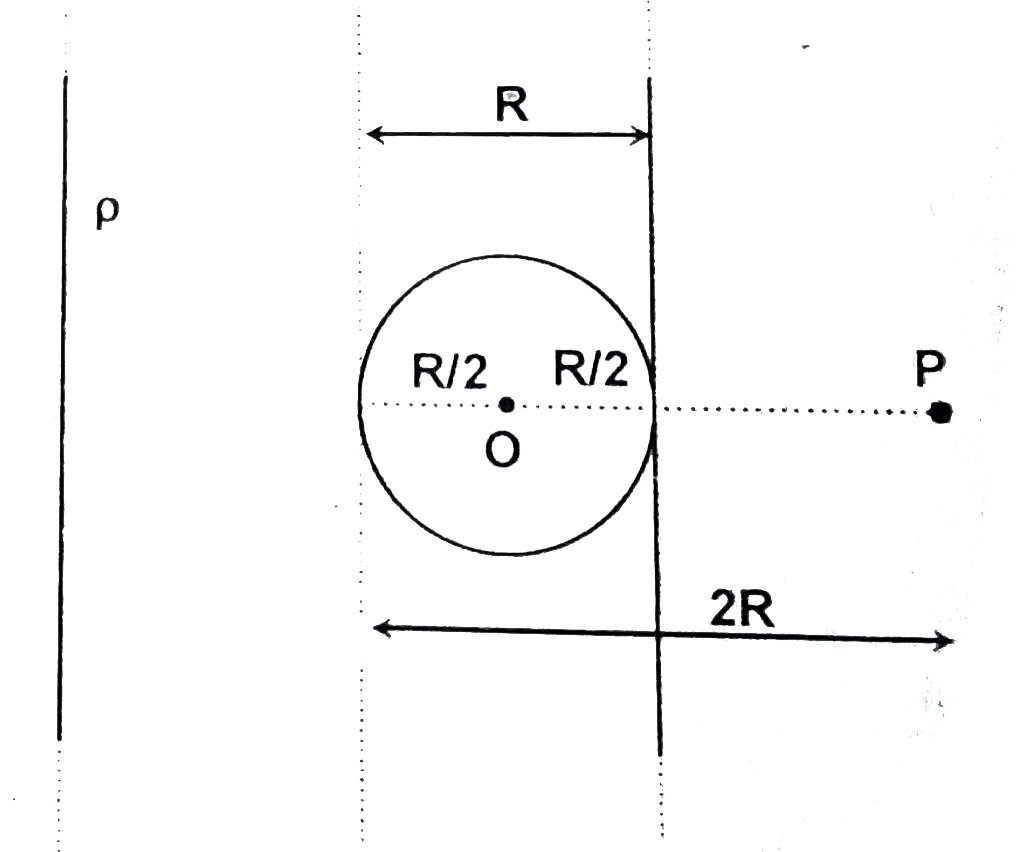 A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0
A23rhpR54ɛ0B23rhpR108ɛ0C25ρR54ɛ0D25ρR108ɛ0A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of theseA positively charged sphere of radius r0 carries a volume charge density ρE (Figure). A spherical cavity of radius r0/2 is then scooped out and left empty, as shown. What is the direction and magnitude of the electric field at point B?
 A17ρr054∈0leftBρ06∈0leftC17ρr054∈0rightDρr06∈0right
A17ρr054∈0leftBρ06∈0leftC17ρr054∈0rightDρr06∈0right
An infinitely long solid cylinder of radius R with uniform volume charge density ρ has a spherical cavity of radius R2 with its centre on the axis of the cylinder as shown in the figure. The magnitude of the electric field at a point P which is at a distance 2R from the axis of the cylinder is given by 23ρR6Kε0. What is the value of K ?
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
View SolutionAn insulated sphere of radius R has a uniform volume charge density λ. The electric field at a point A, which is at distance r from its center is given by (R>r)
View Solution
