Question

A point charge $q=1C$ and mass $1kg$ is projected with speed $10m/s$ in the perpendicular direction of unifrom electric field $E=100V/m$. The value of latus rectum of the path followed by charged particle (in meter) is :

Answer

2

Explanation

Here, `q = 1 C, m = 1 kg`
`v = 10 m//s, E = 100 V//m`.
In fig, `E` is along `OX` and velocity `v` is along `OY`.
Let `P (x,y)` be the position of point charge at any time `t :. Y = v t` or `t = (y)/(v) = (y)/(10)`

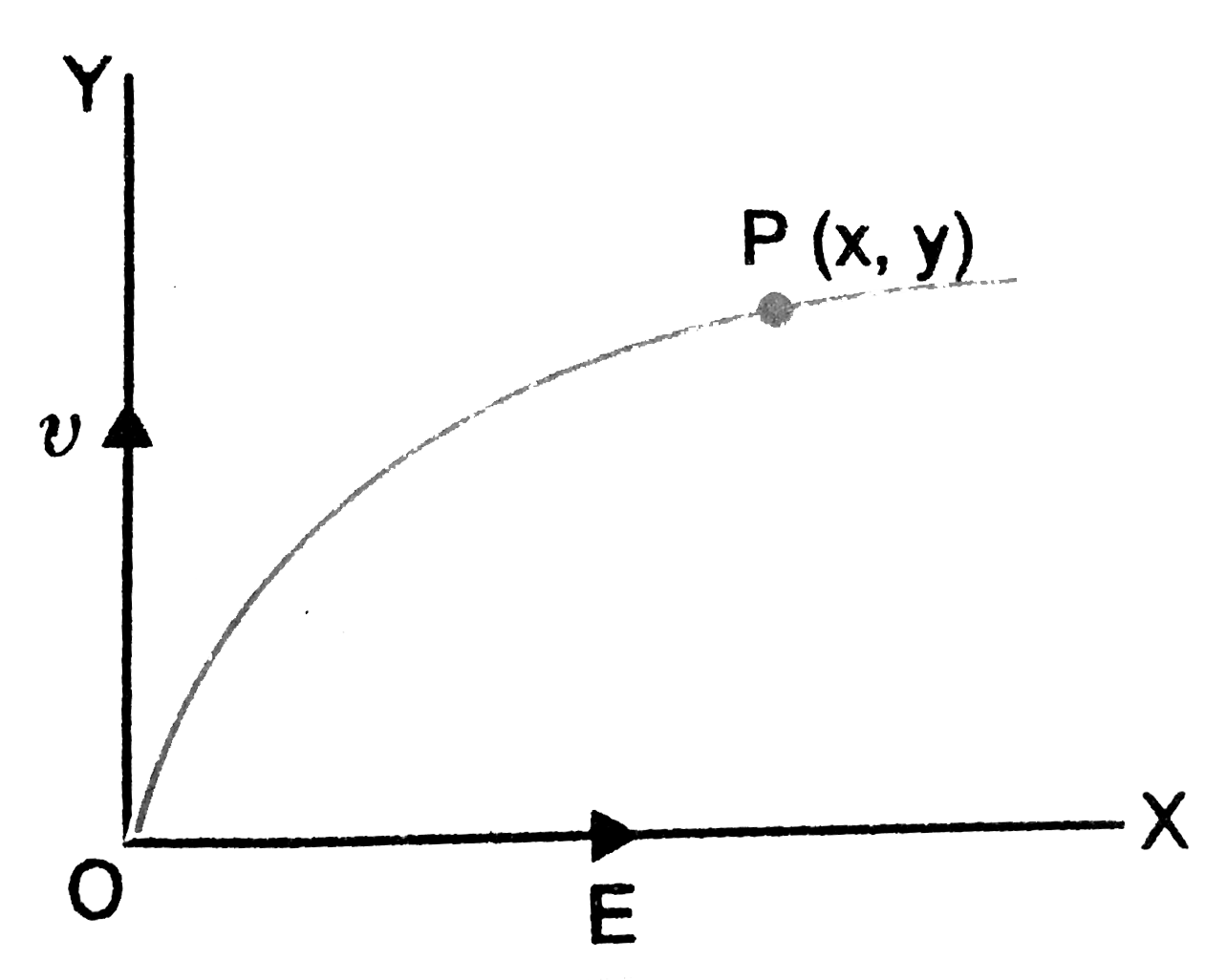
Acceleration along X-axis
`a_(x) = (q E)/(m) = (1xx100)/(1) = 100 m//s^(2)`
As `x = (1)/(2) a_(x) t^(2)`
`:. x = (1)/(2) xx100t^(2) = 50 ((y)/(10))^(2) = (y^(2))/(2)`
`:. y^(2) = 2x`
Which is the equation of a parabola. Comapare with the stantdard equaction of parabola , `y^(2) = 4 ax`, we find `4a = 2m`, which is the length of latus rectum of parabola.