Two conductors of conductnaces G1 and G2 are connected in series. They are connected in parallel to another conductor of conductance G3. Determine their equivalent conductance.
Let R1,R2 and R3 be the resistances of conductors of conductances G1,G2 and G3 respectively.
Here R1=1G1,R2=1G2,R3=1G3 The effective resistance between A to B is
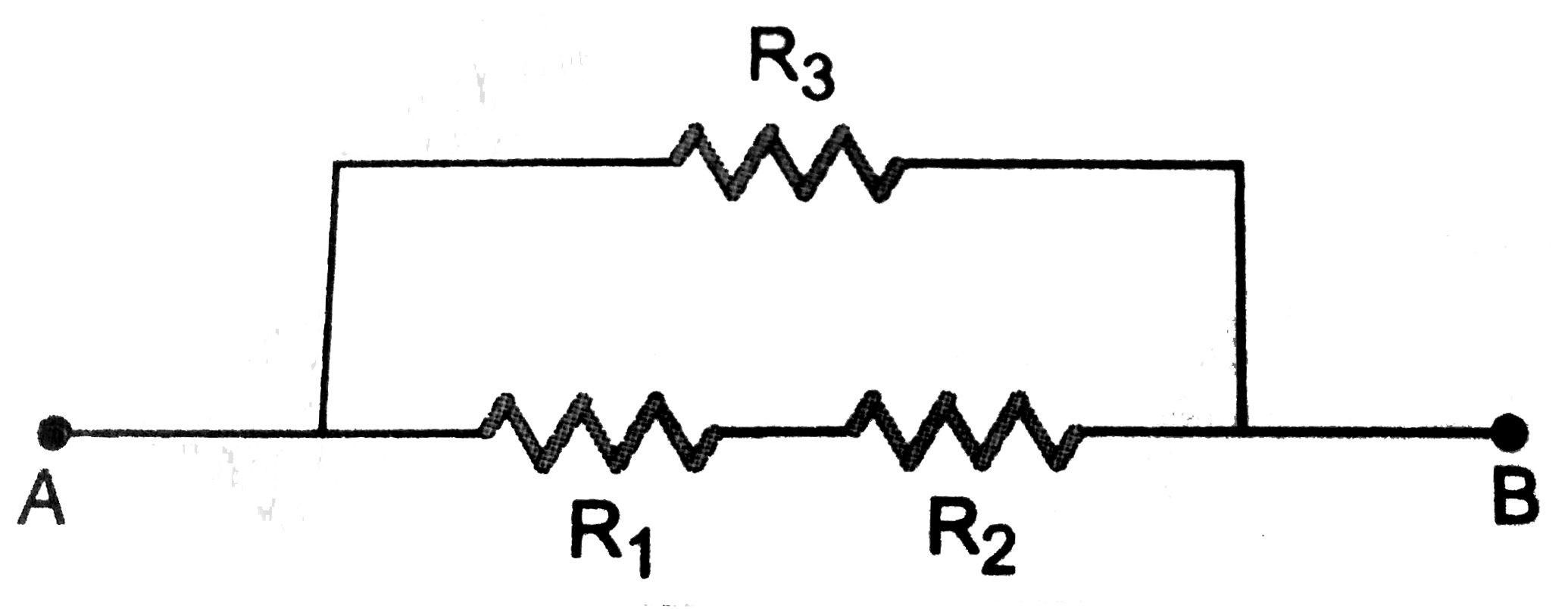
R=R3×(R1+R2)R3+(R1+R2)
∴ Effective conductance,
G=1R=R3+(R1+R2)R3×(R1+R2)
∴G=1G3+1G1+1G21G3×(1G1+1G2)
G1G2+G2G3+G1G3(G2+G1)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
2, 4 and 6 S are the conductance of three conductors. When they are joined in parallel, their equivalent conductance will be
A12 SB(1/12)SC(12/11)SD(11/12)SThree identical condensers are connected together in four different ways. First all of them are connected in series and the equivalent capacity is C1. Next all of them are connected in parallel and the equivalent capacity is C2. Next two of them are connected in series and the third one connected in parallel to the combination and the equivalent capacity is C3. Next two of them are connected in parallel and the third one connected in series with the combination and the equivalent capacity is C4. Which of the following is correct ascending order of yhe equivalent capacities ?
AC1<C3<C4<C2BC1<C4<C3<C2CC2<C3<C4<C1DC2<C4<C3<C1 Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2AStatement I is true, Statement II is true and Statement II is the correct explanation for statement I.BStatement I is true, statement II is true and statement II NOT the correct explanation for Statement ICStatement I is true, Statement II is false.DStatement I is false, statement II is true.
Two conductors of resistance R1(50±2) ohm and R2=(100±4) ohm are connected in (a) series and (b) parallel. Find the equivalent resistance.
View Solution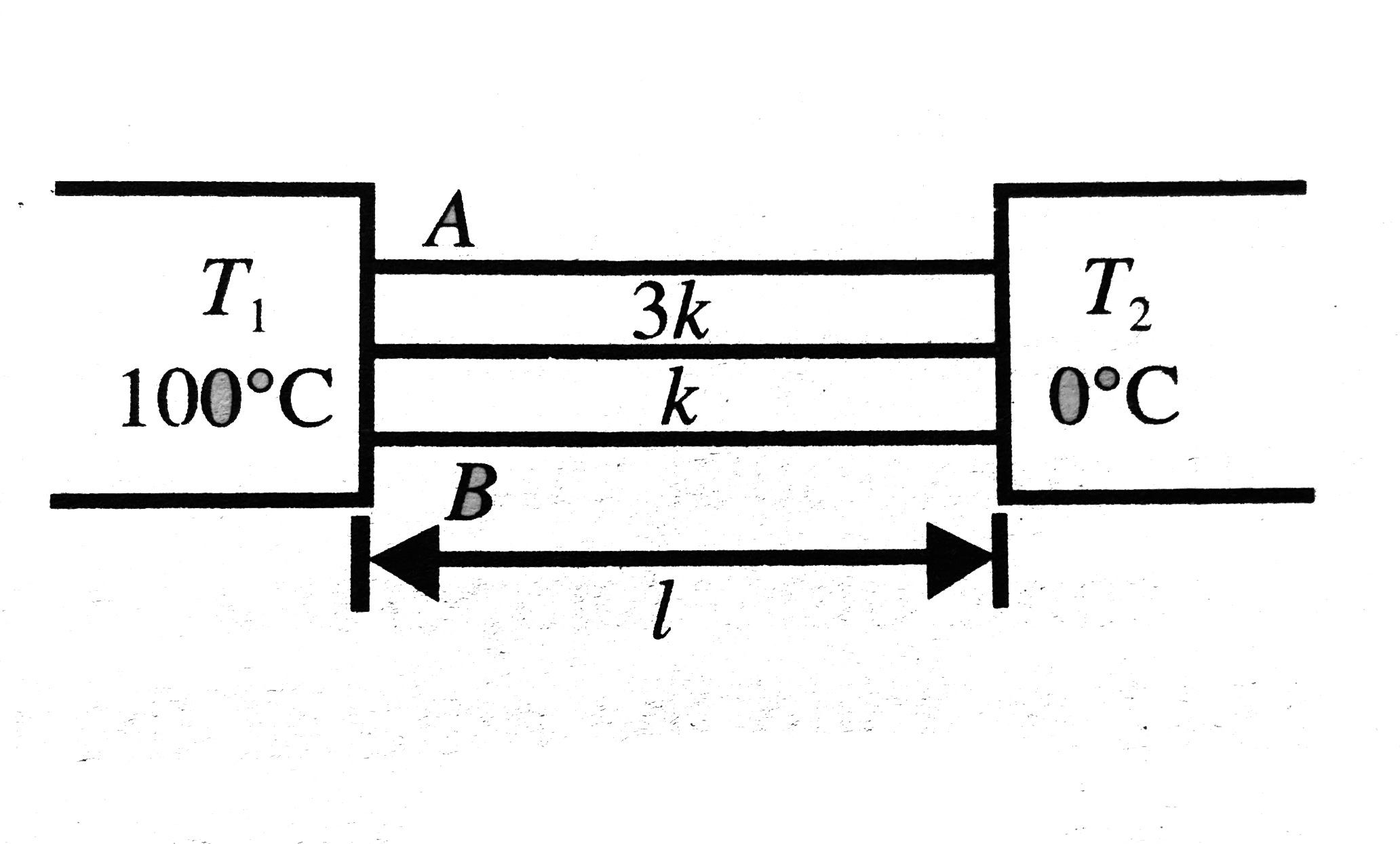
Two conductors A and B given in previous problem are connected in parallel as shown in Fig.
i. Determine the equivalent thermal resistance.
ii. Determine the heat current in each rod.
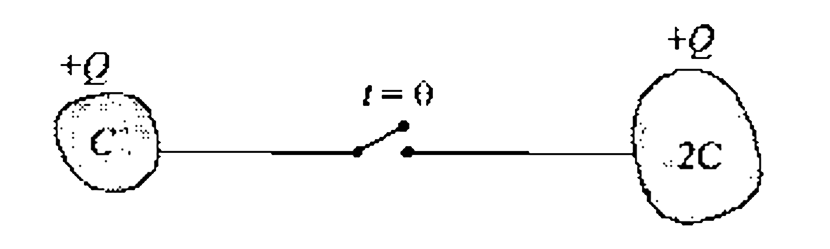
View SolutionThere are two conductors of capacitance C and 2C are charged equally with charge +Q each and connected with a thin conducting wire and a switch as shown in figure. Find the final charges on the conductors after closing the switch.
View SolutionTwo small conductors A and B are given charges q1andq2 respectively. Now they are placed inside a hollow metallic conductor C carrying a charge Q. If all the three conductors A, B and C are connected by a conducting wire as shown, the charges on A,B and C will be respectively :

View SolutionTwo identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
View Solution
