A battery has an emf E and internal resistance r. A variable resistance R is connected across the terminals of the battery. Find the value of R such that (a) the current in the circuit id maximum (b) the potential difference across the terminals is maximum.
To solve the problem, we need to analyze the circuit consisting of a battery with an electromotive force (emf) E and internal resistance r, connected to a variable resistance R. We will find the value of R for two scenarios: (a) when the current in the circuit is maximum, and (b) when the potential difference across the terminals is maximum.
1. Understanding the Circuit:
The total resistance in the circuit is the sum of the internal resistance r and the variable resistance R. The current I flowing through the circuit can be expressed using Ohm's law:
I=ER+r
2. Maximizing the Current:
To maximize the current I, we need to minimize the total resistance R+r. Since r is a fixed value (the internal resistance of the battery), we should set R to its minimum value. The minimum value of R is 0 (short circuit condition).
3. Conclusion:
Therefore, for maximum current:
R=0Ω
Part (b): Finding R for Maximum Potential Difference
1. Potential Difference Across R:
The potential difference V across the variable resistance R can be expressed as:
V=I⋅R=(ER+r)R
Simplifying this gives:
V=ERR+r
2. Maximizing the Potential Difference:
To find the value of R that maximizes V, we can differentiate V with respect to R and set the derivative to zero. However, we can also use the concept of the maximum power transfer theorem, which states that maximum power (and thus maximum potential difference across R) occurs when the load resistance R is equal to the internal resistance r.
3. Conclusion:
Therefore, for maximum potential difference:
R=r
Final Answers:
- (a) For maximum current, R=0Ω.
- (b) For maximum potential difference, R=r.
The total resistance in the circuit is the sum of the internal resistance r and the variable resistance R. The current I flowing through the circuit can be expressed using Ohm's law:
I=ER+r
To maximize the current I, we need to minimize the total resistance R+r. Since r is a fixed value (the internal resistance of the battery), we should set R to its minimum value. The minimum value of R is 0 (short circuit condition).
Therefore, for maximum current:
R=0Ω
The potential difference V across the variable resistance R can be expressed as:
V=I⋅R=(ER+r)R
Simplifying this gives:
V=ERR+r
To find the value of R that maximizes V, we can differentiate V with respect to R and set the derivative to zero. However, we can also use the concept of the maximum power transfer theorem, which states that maximum power (and thus maximum potential difference across R) occurs when the load resistance R is equal to the internal resistance r.
Therefore, for maximum potential difference:
R=r
- (a) For maximum current, R=0Ω.
- (b) For maximum potential difference, R=r.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems3videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A7videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-29videos
COMMUNICATION SYSTEMS
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Shown n batteries connected to form a circuit. The resistances denote the internal resistances of the batteries which are related to the emf's as ri=k(ε)iwhere K is a constant. The solid dots represent the terminals of the batteries. Find (a)the current through the circuit and (b) the potential difference between the terminals of the ith battery.
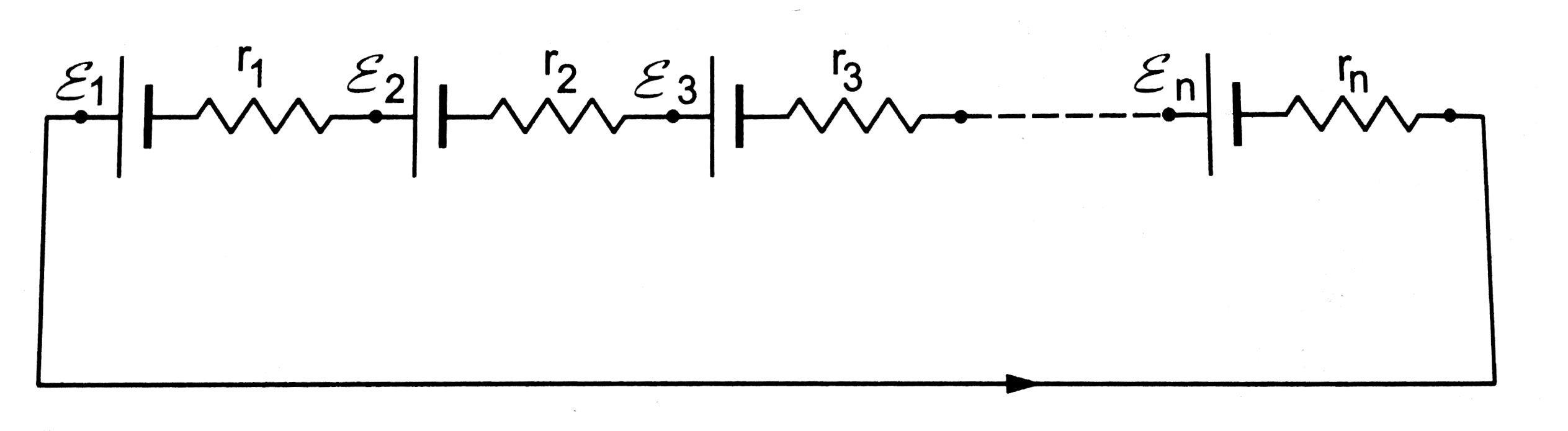 View Solution
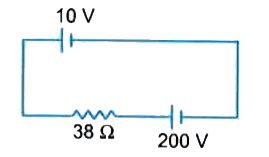
View SolutionA 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38 Ω as shown in the Fig. Find the value of the current in circuit.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A battery is of emt E and internal resistance r. The value of external resistance R so that the power across eternal resistance is maximum :
ARB2RCR/2DR/4 - Question 2 - Select One
A battery of emf E has an internal resistance r. A variable resistacne R is connected to the terminals of the battery. A current i is drawn from the battery. V is the terminal potential difference. If R alone is gradually reduced to zero, which of the following best describes i and V?
Ai approaches zero, V approaches EBi approaches Er, V approaches zeroCi approaches Er, V approaches EDi approaches infinity, Er, V approaches E - Question 3 - Select One or More
A battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
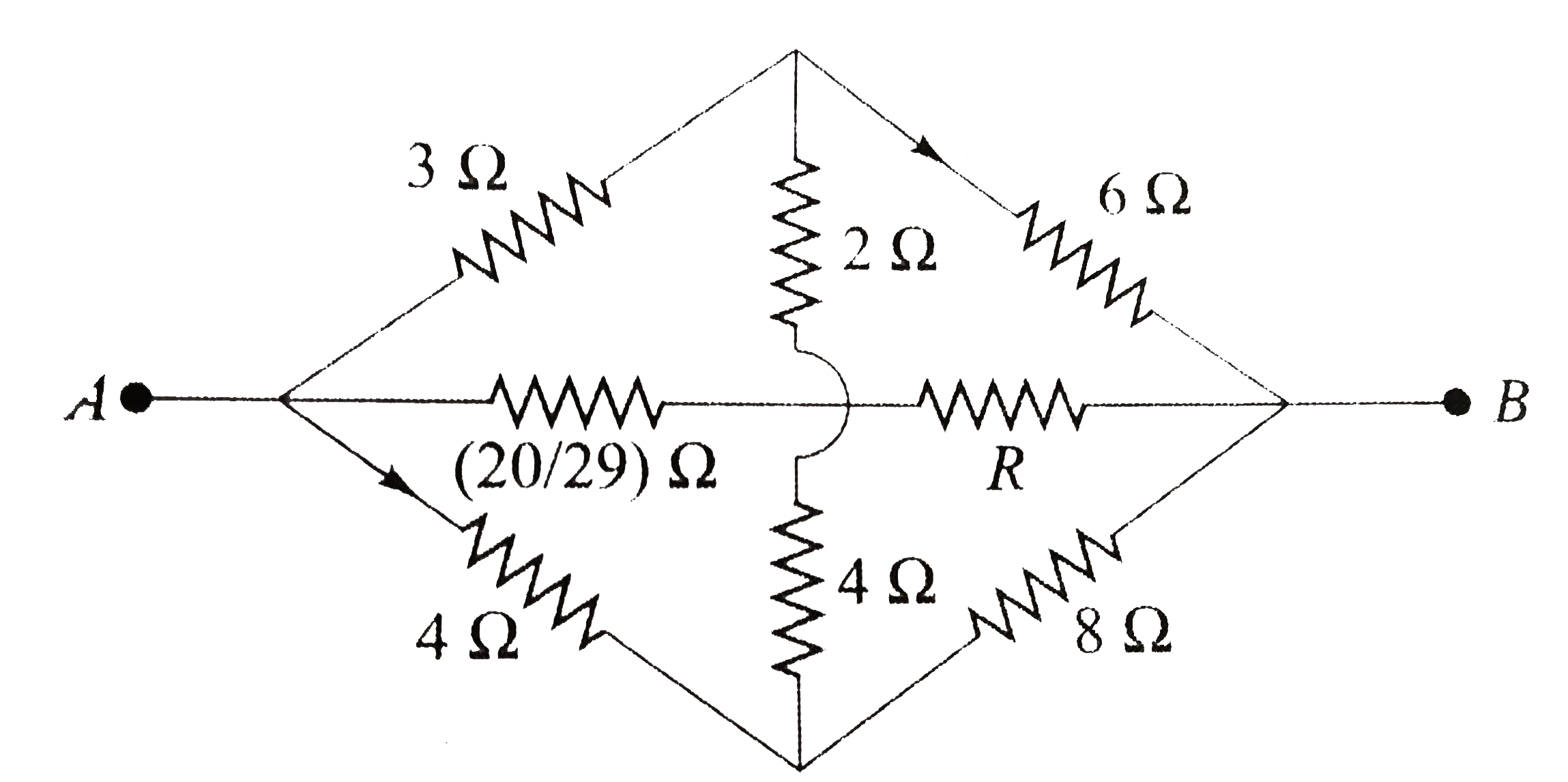 . AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
. AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
A battery of emf E and internal resistance r is connected to a variable resistor R as shown in figure. Which one of the following is true ?
 View Solution
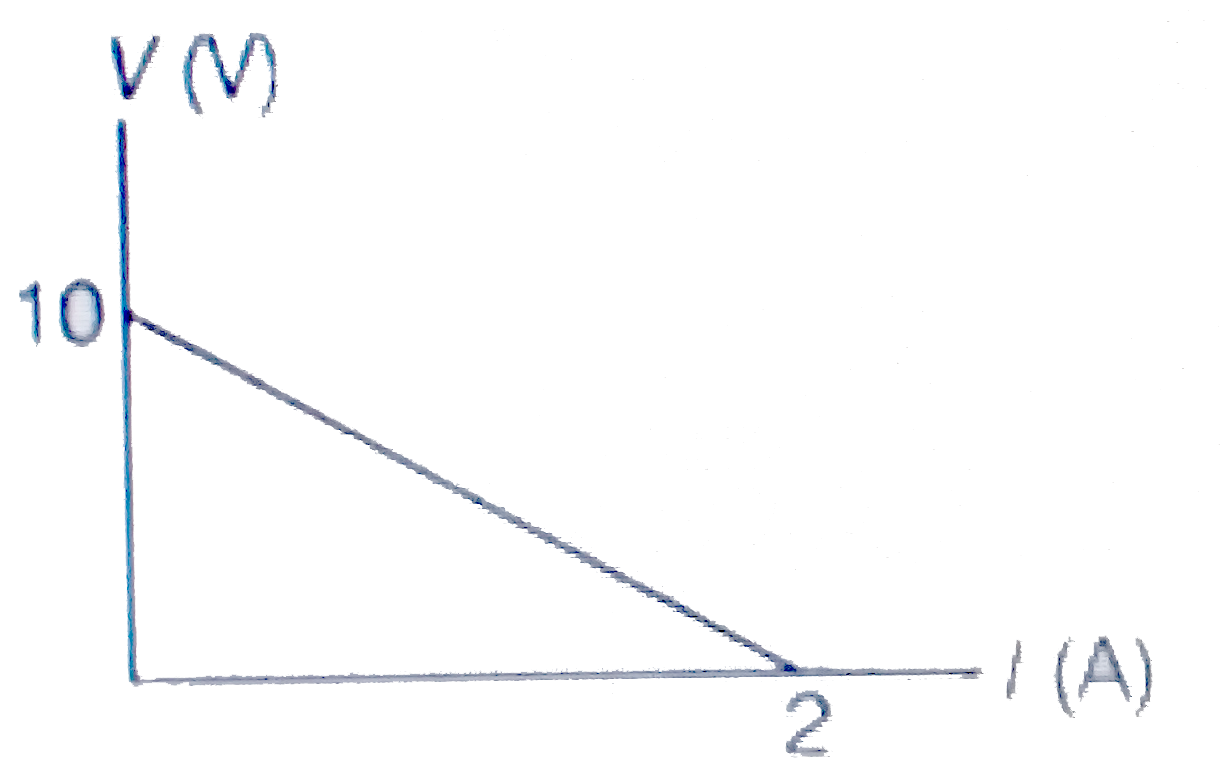
View SolutionA battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference across the termainals of the battery (V). Maximum power developed across the resistance R is
 View Solution
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionCell A has emf 2 E ad internal resistance 4 r. Cell B has emf E and internal resistance r. The negative of A is connected to the positive of B and a load resistance of R is connected across the battery formed. If the terminal potential difference across A is zero, then R is equal to
View SolutionA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View Solution

