A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, versesR.
To solve the problem of plotting the potential difference (P.D.) across an external resistance R connected to a cell with an electromotive force (EMF) E and internal resistance r, we can follow these steps:
Step 1: Understand the Circuit
We have a circuit consisting of a cell with EMF E and internal resistance r connected to an external resistor R. The total resistance in the circuit is R+r.
Step 2: Write the Expression for Current
The current I flowing through the circuit can be expressed using Ohm's Law:
I=ER+r
Step 3: Write the Expression for Potential Difference
The potential difference V across the external resistor R can be calculated using the formula:
V=I⋅R
Substituting the expression for I:
V=(ER+r)R
This simplifies to:
V=ERR+r
Step 4: Analyze the Equation
The equation V=ERR+r shows how the potential difference V varies with the external resistance R. Here, E and r are constants.
Step 5: Plotting the Graph
To plot the graph of V versus R:
1. Choose fixed values for E and r. For example, let E=5V and r=2Ω.
2. Calculate V for various values of R (e.g., R=0,1,2,3,4,5,10Ω).
3. Plot these values on a graph with R on the x-axis and V on the y-axis.
Step 6: Interpret the Graph
- As R increases, V initially increases.
- However, as R becomes very large compared to r, V approaches E but never exceeds it.
- The graph will show a curve that rises initially and then levels off, approaching the value of E.
Final Graph Characteristics
- The graph will start from the origin (0,0) and rise to a maximum value of E as R increases.
- The slope of the graph will decrease as R increases, indicating diminishing returns in potential difference as resistance increases.
We have a circuit consisting of a cell with EMF E and internal resistance r connected to an external resistor R. The total resistance in the circuit is R+r.
The current I flowing through the circuit can be expressed using Ohm's Law:
I=ER+r
The potential difference V across the external resistor R can be calculated using the formula:
V=I⋅R
Substituting the expression for I:
V=(ER+r)R
This simplifies to:
V=ERR+r
The equation V=ERR+r shows how the potential difference V varies with the external resistance R. Here, E and r are constants.
To plot the graph of V versus R:
1. Choose fixed values for E and r. For example, let E=5V and r=2Ω.
2. Calculate V for various values of R (e.g., R=0,1,2,3,4,5,10Ω).
3. Plot these values on a graph with R on the x-axis and V on the y-axis.
- As R increases, V initially increases.
- However, as R becomes very large compared to r, V approaches E but never exceeds it.
- The graph will show a curve that rises initially and then levels off, approaching the value of E.
- The graph will start from the origin (0,0) and rise to a maximum value of E as R increases.
- The slope of the graph will decrease as R increases, indicating diminishing returns in potential difference as resistance increases.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
.A cell of emf E and internal resistance r is connected across a variable resistor. Plot a graph showing variation of terminal voltage V of cell versus the current.
View SolutionA cell of emf ' ε ' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing the variation of terminal potential 'V' with resistance R. Predict from the graph the condition under which 'V' becomes equal to 'ε'
View Solution
Knowledge Check
A cell of internal resistance r connected across an external resistance R can supply maximum current when
AR=rBR>rCR=r2DR=0A cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
A1/nB1/(n+1)Cn/(n+1)D(n+1)/nA cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
A B
B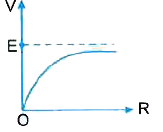 C
C D
D
A cell of emf 'ε' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing variation of terminal voltage 'V' of the cell versus the current 'l'. Using the plot, show how the emf of the cell and its internal resistance can be determined.
View SolutionA cell of emf ε and internal resistance r is connected across a variable resistor R. Plot a graph showing variation of terminal voltage V of the cell versus the current I. Using the plot, show how the emf of the cell and its internal resistance can be determined.
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution
