Question

In order to increase the resistance of a given wire of uniform cross section to four times its value, a fraction of its length is stretched uniformly till the full length of the wire becoes $\frac{3}{2}$ times the original length. What is the value of this fraction?

Explanation

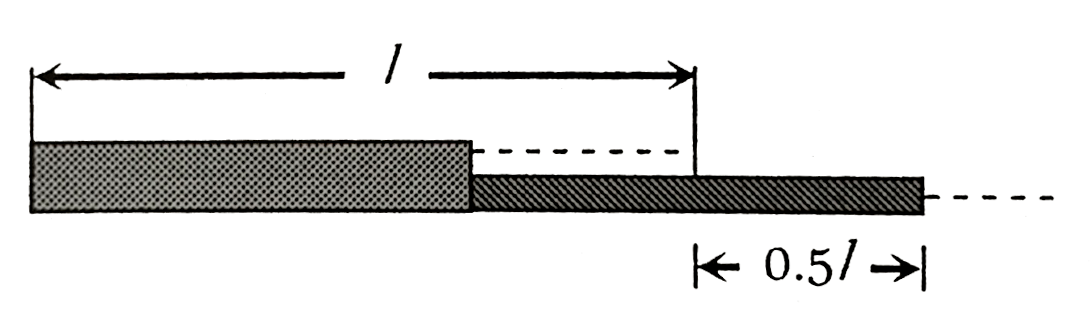
Let `l` be the origin length of the wire suppose a portion `(l -x)` of the wire is streched so that the final length of the whole wire becomes `1.5 l` Fig.2 (HT).6.
Let `R_(1),R_(2)` = resistance of the wire before and after stretching.
`A_(1),A_(2)` = Area of cross section of the wire of portion of length x and `(1.5 l -x)` respectively after stretching.
`rho` = resistivity of the material of the wire.
As per question `= R_(2) = 4 R_(1) = 4 rho l//A_(1)`
But, `R_(2)=(rho(1.5l-x))/(A_(2))+(rhox)/(A_(1))=(4 rhol)/(A_(1))`
On stretching the wire, the total volume of the wire remains constant, therefore
`A_(1)l=A_(2) (1.5 l -x)+ A_(1) x`....(iii)
On solving (ii) and (iii), we get, `x//l = 7//8`
`:.` Fraction of length of wire elongated `= (l-x)/(l)=1 - (x)/(l) =-(7)/(8) = (1)/(8)`