At 0∘C the electron of conductor of a conductor B is n times that of conductor A temperature coefficient of resistance for A and B are α1andα2 respectively the temperature coefficient of resistance of a circuit segment constant A and B in series is
nα1+nα21+n
nα1−nα21+n
α1+nα21+n
α2+nα11+n
The correct Answer is:C
Let R1 and R2 be the resistance of A and B at 0∘C and R'1 and R'2 be the resistances of A and B at t∘C. Then
R2=nR1,R'1=R1(1+α1t),R'2=R2(1+α2t)
When resistances are connected in series, then
R's=R'1+R'2=R1(1+α1t),R'2=R2(1+α2t)
or R's=R1[(1+n)+(α1+nα2)t]......(i)
Let αs be the temp. coeff. of resistance of Standard equation for series combination is
R's=(R1+R2)(1+αst)=(R1+nR1)(1+αst)
=R1(1+n)(1+αst)
=R1[(1+n)+(1+n)αst)....(ii)
Comparing (i) and (ii), we have
(α1+nα2)=(1+n)αsorαs=α1+nα21+n
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
At the tempearture 0∘C the electric resistance of conductor 2 is η times that of conductor 1. Thier temperatures coeficients of resistance are equal to α2 and α1 respectively. Find the tempearture coefficient of resistance of a circuit segment consisting of these two conductors when they are connected
(a) In series , (b) In parallel .
View SolutionAt the temperature 0∘C the electron of conductor B is n times that of condoctor A temperaturte coefficient of resistance are equal to α2andα1 respectively find the resistance and A temperaturte coefficient of resistance of a segment of these two condustore when they are conected in series
View Solution
Knowledge Check
The temperature coefficient of resistance of a conductor is
APositive alwaysBNegative alwaysCzeroDInfiniteThe temperature coefficient of resistance of a semi conductor is
AIs always positiveBIs always negativeCIs zeroDMay be positive or negative or zeroTwo conductors have the same resistance at 0∘C but the temperature coefficients of resistance are α1andα2 The respective temperature coefficients of their series and parallel combinations are nearly
Aα1+α22,α1+α2Bα1+α2,α1+α23Cα1+α23,α1+α2Dα1+α22,α1+α22
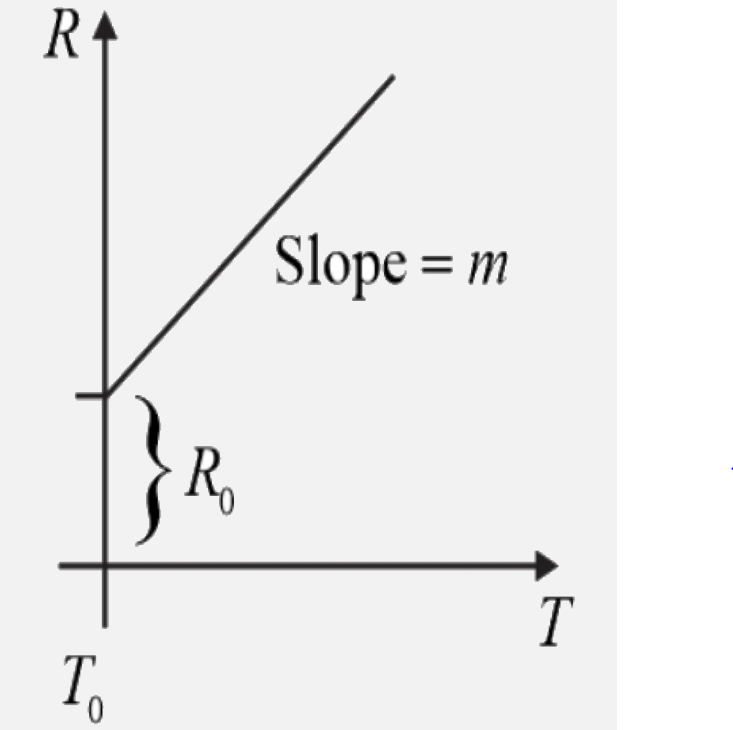
Variation of resistance of the conductor with temperature is shown . Temperature coefficient of the conductor is
View SolutionTwo conductors have the same resistance at 0∘C but their temperature coefficient of resistanc are α1andα2. The respective temperature coefficients of their series and parallel combinations are nearly
View SolutionTwo wires of resistance R1 and R2 have temperature coeficient of resistance α1 and α2 respectively. These are joined in series. The effeictive temperature coefficient of resistance is
View SolutionCoefficient of linear expnsion of material of resistor is α . Its temperature coefficient of resistivity and resistance are αp and αR respectively , the correct relation is .
View SolutionThe ratio of the resistances of a conductor at a temperature of 15∘C to its resistance at a temperature of 37.5∘C is 4:5. The temperature coefficient of resistance of the conductor is
View Solution