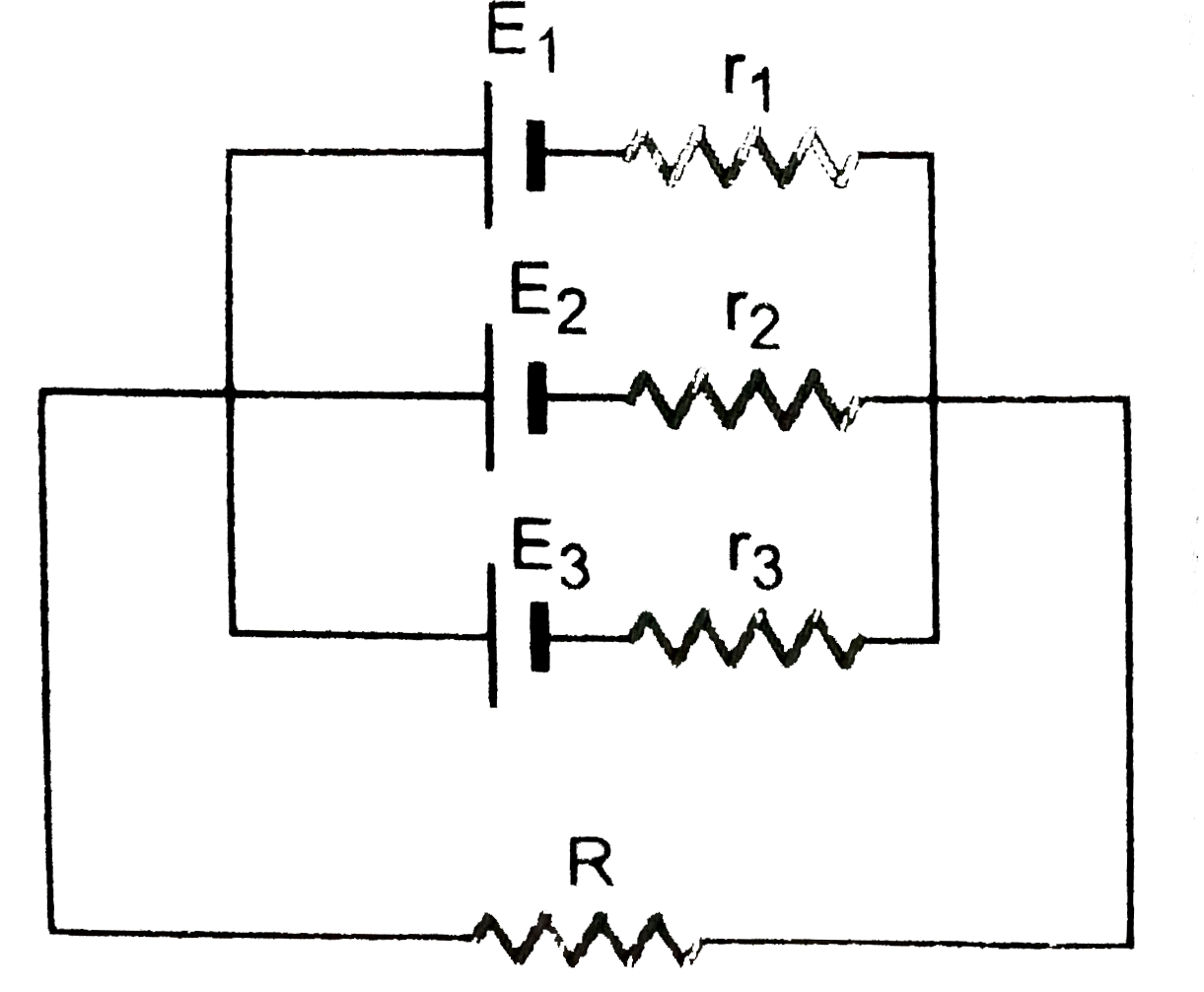
Three cell are connected in parallel with their like poles connected together with wires of negligible resistance .If the emf of the internal resistance are 4,3and2Ω respectively, Find the current through each cell
The correct Answer is:l1=−213A;l2=−713Aandl3=913A
To solve the problem of finding the current through each cell in a parallel circuit with given internal resistances, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have three cells connected in parallel with their like poles connected together. The EMF (electromotive force) and internal resistances of the cells are given as follows:
- Cell 1: EMF = 4V, Internal Resistance = 4Ω
- Cell 2: EMF = 3V, Internal Resistance = 3Ω
- Cell 3: EMF = 2V, Internal Resistance = 2Ω
Step 2: Apply Kirchhoff's Current Law
According to Kirchhoff's Current Law, the total current entering a junction must equal the total current leaving the junction. Let the currents through the cells be:
- I1 for Cell 1
- I2 for Cell 2
- I3 for Cell 3
Thus, we can write:
I1+I2+I3=0
(assuming the currents are flowing out of the junction).
Step 3: Apply Kirchhoff's Voltage Law
For each cell, we can apply Kirchhoff's Voltage Law to set up equations based on the voltage drops across the internal resistances. The voltage drop across each cell can be expressed as:
- For Cell 1: 4−I1⋅4=0
- For Cell 2: 3−I2⋅3=0
- For Cell 3: 2−I3⋅2=0
Step 4: Rearranging the Equations
From the equations above, we can express the currents in terms of the EMF and internal resistance:
1. I1=44=1 A
2. I2=33=1 A
3. I3=22=1 A
Step 5: Solve the System of Equations
Now we can substitute these values into the first equation:
I1+I2+I3=0
This leads us to:
1+1+1=0
This indicates that we need to consider the direction of the currents. Since they are flowing in opposite directions, we can assign negative values:
- I1=−1 A
- I2=−1 A
- I3=−1 A
Step 6: Final Result
Thus, the currents through each cell are:
- Current through Cell 1: I1=−1 A
- Current through Cell 2: I2=−1 A
- Current through Cell 3: I3=−1 A
We have three cells connected in parallel with their like poles connected together. The EMF (electromotive force) and internal resistances of the cells are given as follows:
- Cell 1: EMF = 4V, Internal Resistance = 4Ω
- Cell 2: EMF = 3V, Internal Resistance = 3Ω
- Cell 3: EMF = 2V, Internal Resistance = 2Ω
According to Kirchhoff's Current Law, the total current entering a junction must equal the total current leaving the junction. Let the currents through the cells be:
- I1 for Cell 1
- I2 for Cell 2
- I3 for Cell 3
I1+I2+I3=0
(assuming the currents are flowing out of the junction).
For each cell, we can apply Kirchhoff's Voltage Law to set up equations based on the voltage drops across the internal resistances. The voltage drop across each cell can be expressed as:
- For Cell 1: 4−I1⋅4=0
- For Cell 2: 3−I2⋅3=0
- For Cell 3: 2−I3⋅2=0
From the equations above, we can express the currents in terms of the EMF and internal resistance:
1. I1=44=1 A
2. I2=33=1 A
3. I3=22=1 A
Now we can substitute these values into the first equation:
I1+I2+I3=0
This leads us to:
1+1+1=0
This indicates that we need to consider the direction of the currents. Since they are flowing in opposite directions, we can assign negative values:
- I1=−1 A
- I2=−1 A
- I3=−1 A
Thus, the currents through each cell are:
- Current through Cell 1: I1=−1 A
- Current through Cell 2: I2=−1 A
- Current through Cell 3: I3=−1 A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Three cells are connected in parallel with their like poles connected together with wires of negligible resistance. If the emfs of the cells are 2, 1 an 4 V respectively and their internal resistances are 4,3 and 2Ω respectively, find the current through each cell.
View SolutionThree cells are connected in parallel, with their like poles connected together, with wires of negligible resistance. If the emf of the cell are 2V, 1V and 4V and if their internal resistance are 4Ω,3Ωand2Ω respectively, find the current through each cell.
View Solution
Knowledge Check
Two cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
A0.87 AB1.29 AC1.00 AD2.29 AThree cells are connected to an external resistance as shown in the figure. Each of the cells has emf 10 V and internal resistance 2Ω.
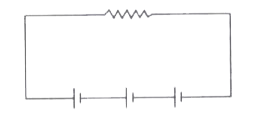
If the external resistance is 6Ω. Find the current in the circuit.A2AB2.5 AC3AD3.5 AIn a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
A5/22 AB15/22 AC3/7 AD5/9 A
If three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
View SolutionA bulb of resistance 5Ω is connected to a battery of emf 4.2 V and internal resistance 1Ω. Find the current through the bulb.
View SolutionFour resistors of 12Ω each are connected in parallel . Three such combinations are then connected in series. What is the total resistance ? If a battery of 9 V emf and negligible internal resistance is connected across the networks, find the current flowing through of each resistors.
View SolutionTwo identical cells, whether connected in series or in parallel with each other send the same current through an external resistance R. The internal resistence of each cell is
View SolutionTwo identical cells whether connected in parallel or in series gives the same current, when connected to an external resistance 1.5Ω. Find the value of internal resistance of each cell.
View Solution
