Prism 1 of mass m1 and width angle α (see figure) rests on a horizontal surface. Bar 2 of mass m2 is placed on the prism. Assuming the friction to be negligible, find the acceleration of the prism.

Let us draw the force diagram of each body, and on this basic we observe that the prism moves towards right say with an acceleration →w1 and the bar 2 of mass m2 moves down the plane with respect to 1, say with acceleration →w21, then, →w2=→w21+→w1 (figure).
Let us write Newton's second law for both bodies in projection form along positive y2 and x1 axes as shown in the figure.
m2gcosα−N=m2w2(y2)=m2[w21(y2)+w1(y2)]=m2[0+w1sinα]
or, m2gcosα−N=m2w1sinα (1)
and Nsinα=m1w1 (2)
Solving (1) and (2), we get
w1=m2gαcosαm1+m2sin2α=gsinαcosα(m1/m2)+sin2α

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum82videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A heavy mass m slides down a triangular prism of mass M . The prism lies on a horizontal surface and can move along it without friction . What will be the direction of motion of m if the inclination of the hypotenuse of the prism is α with the horizontal ?
View SolutionIn the figure-2.61 a bar of mass m is on the smooth inclined face of the wedge of mass M,the inclination to the horizontal being 0.The wedge is resting on a smooth horizontal plane.Assuming the pulley to be smooth and the string is light and inextensible. Find the acceleration of M,when M and m are always in contact.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
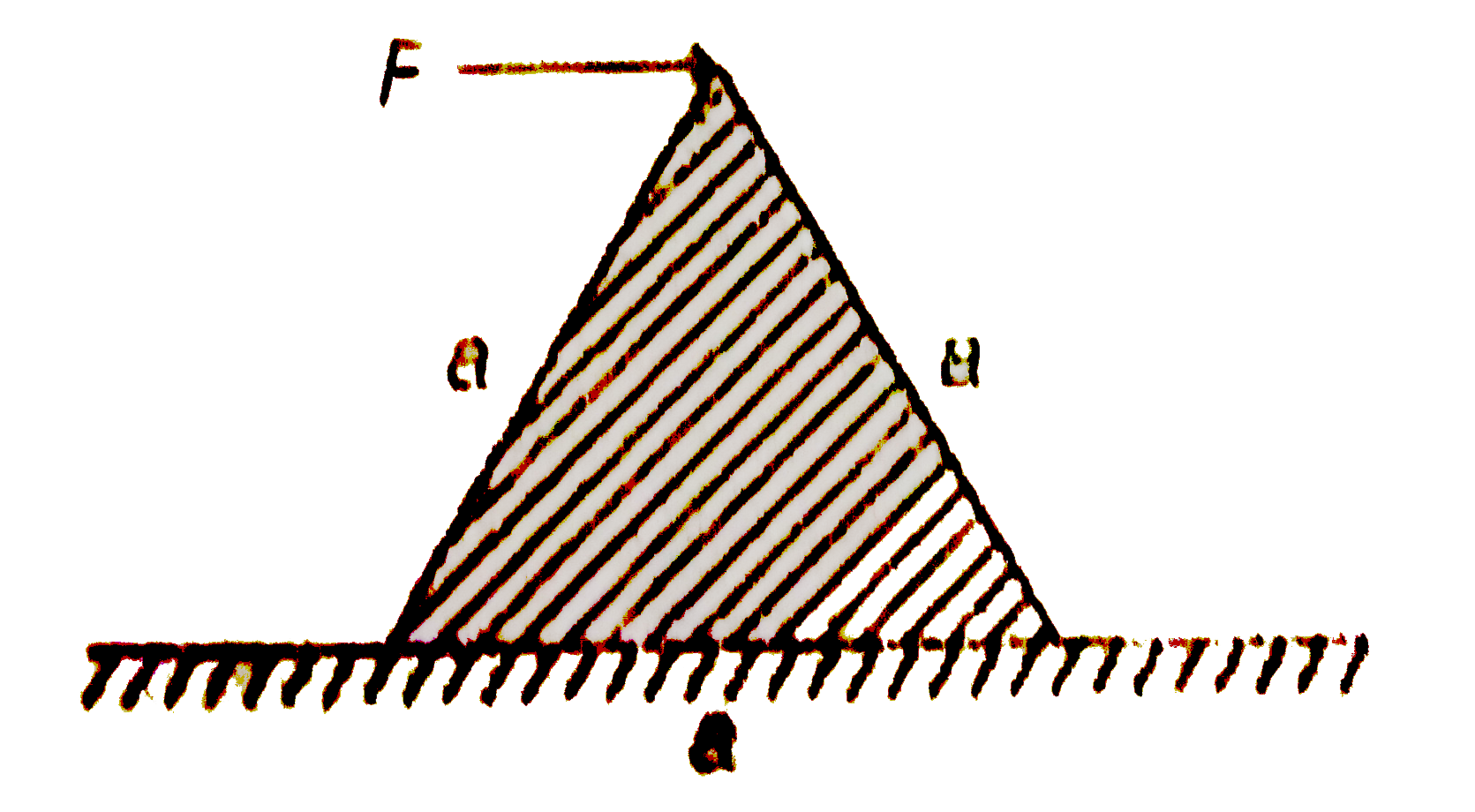 Amg√3Bmg4Cμmg√3Dμmg4
Amg√3Bmg4Cμmg√3Dμmg4 - Question 2 - Select One
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of these - Question 3 - Select One
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
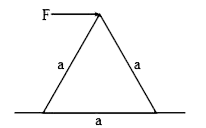 Amg√3Bmg4Cμmg√3Dμmg4
Amg√3Bmg4Cμmg√3Dμmg4
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
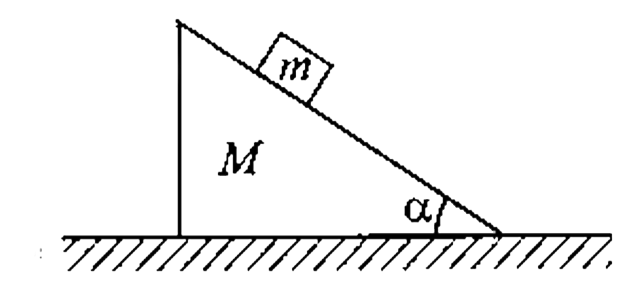 View Solution
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
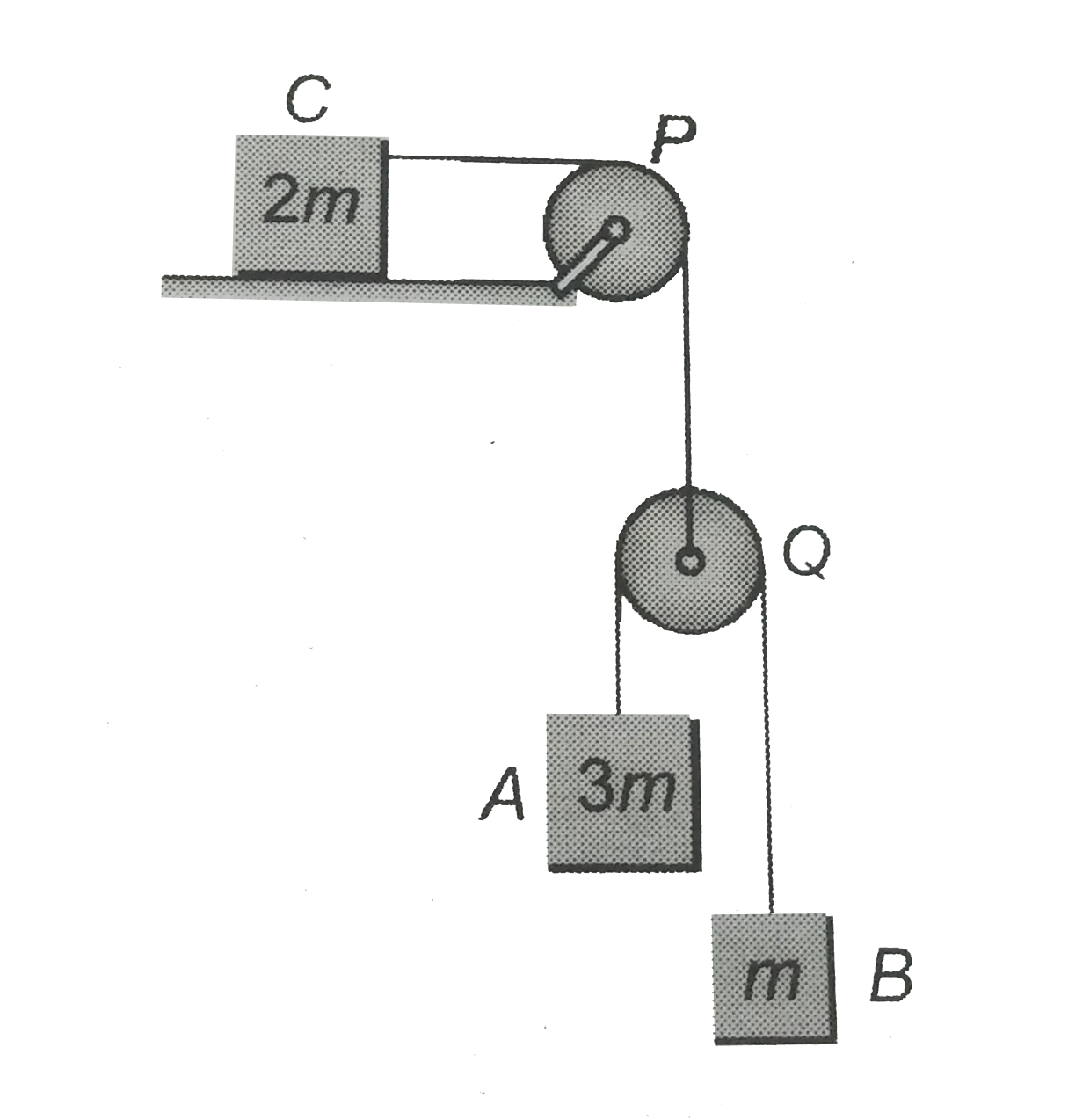 View Solution
View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1
 View Solution
View SolutionAll the surfaces shownin figure are assumed to be frictionless. The block of mass m slides on the prism which in turn slides backwasrd on the horizontal surface. Find the aceleration of the smaller block with respect to the prism.
 View Solution
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
 View Solution
View Solution

