A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of , the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
Let us depict the forces acting on the small sphere m, (at an arbitrary position when the thread makes an angle from the vertical) and write equation via projection on the unit vectors and . From , we have
(as vertical is reference line of angular position)
or
Integrating both the sides:
or,
Hence .(1)
(Eq. (1) can be easily obtained by the conservation of mechanical energy).
From
Using (1) we have
(2)
Again from the Eq. :
or (3)
Hence (using 1 and 3)
(b) Vertical component of velocity
So, (using 1)
For maximum or ,
which yields
Therefore from (2)
(c) We have thus
But in accordance with the problem
So,
or,
or , or,

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum
82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
a small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
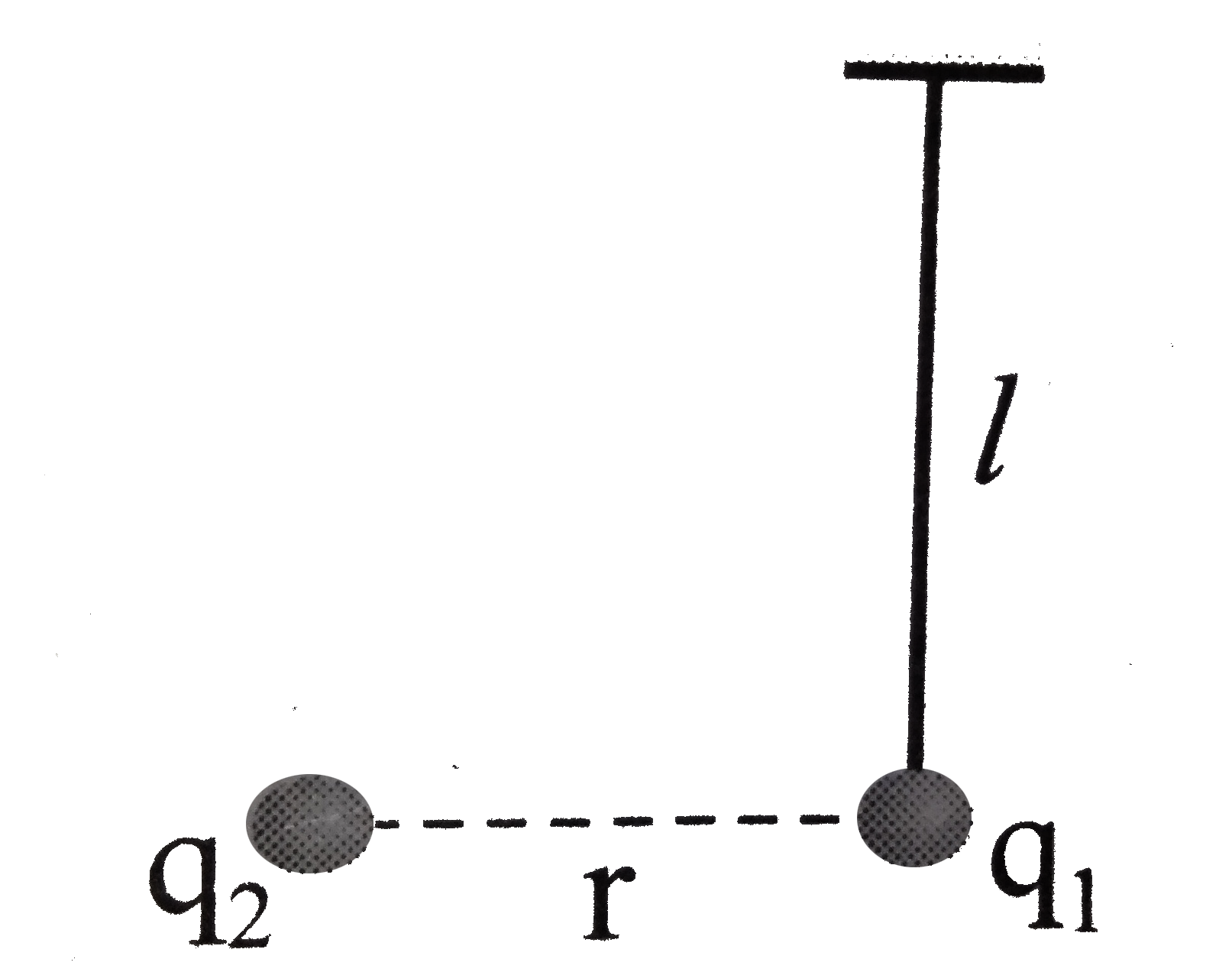
View Solution
Knowledge Check
A small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg.A small sphere of mass m is supended by a thread of length l. It is raised upto the height of suspension with thread fully stretched and released. Then, the maximum tension in thread will be
AmgB2 mgC3 mgD6 mgIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
Aε0(mgq)tanθBε0(2mgq)tanθCε0(mgq)tanθDε0(mg3q)tanθ
A small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View SolutionIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere the surface charge density of the plate -
View SolutionIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
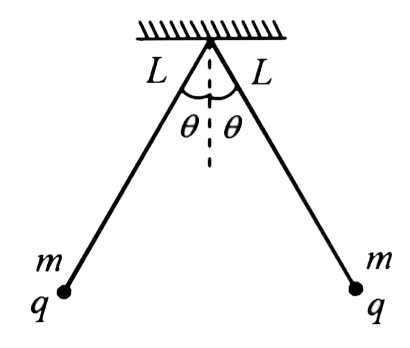
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.

View Solution
