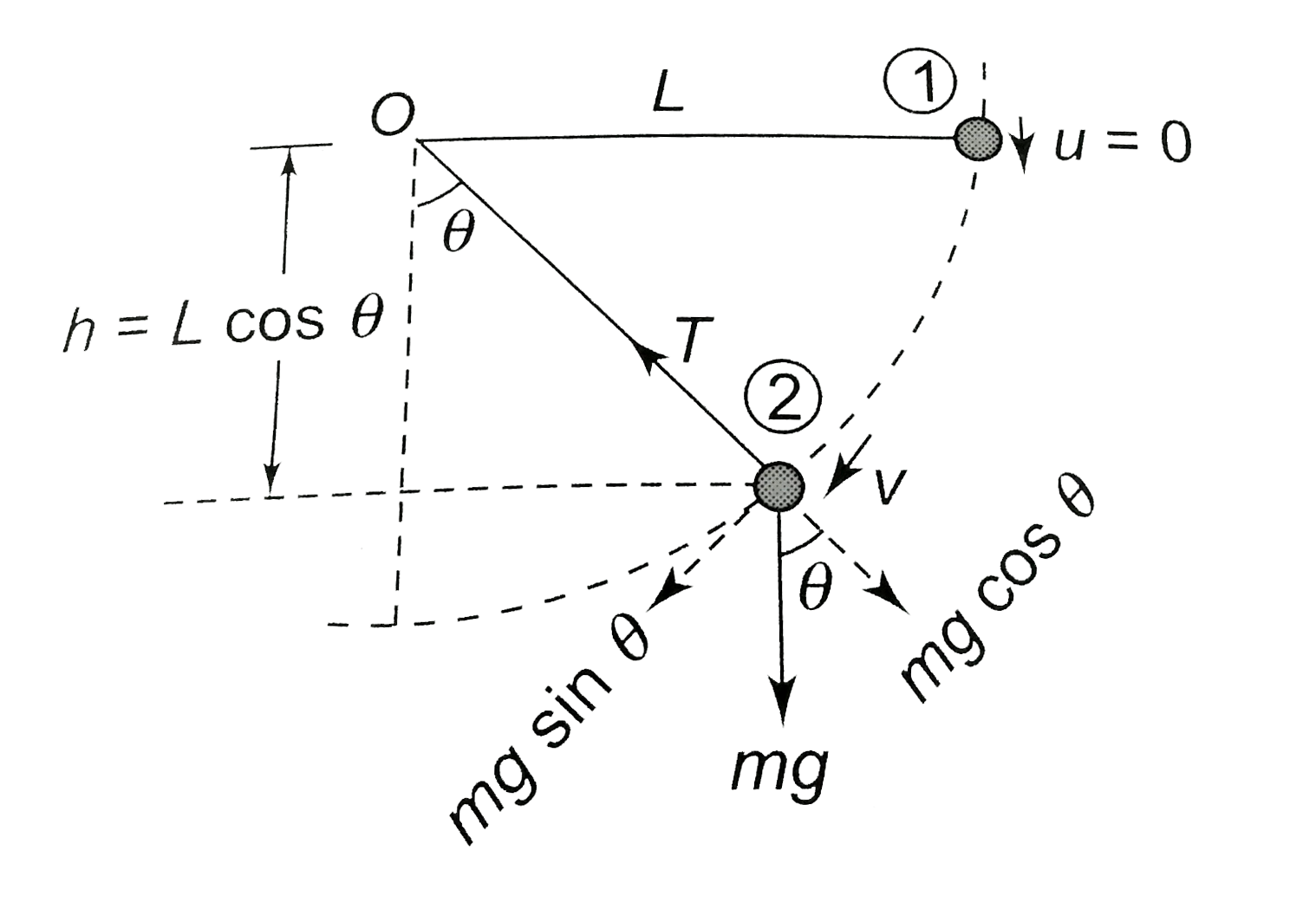
a small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
(a) v2=u2+2gh=0+2gLcosθ
ac=v2L=2gcosθ
at=gsinθ
a=√a2c+a2t=g√1+3cos2θ
Total acceleration: a=g√1+3cos2θ
T−mgcosθ=mv2L=2mgcosθ
T=3mgcosθ
accosθ=atsinθ
2gcos2θ=gsin2θ
implies tan2θ=2
tanθ=√2
cosθ=1√3
θ=cos−1(1√3)
(ii) when θ=0∧(∘), i.e., when the sphere is at the lowest postion, at=0, (since at=gsinθ)
a=ac, directed vertically upwards
(iii) when θ=90∘, i.e., when the string is horizontal,
ac=0(sinceac=u2L)
a=at=gsin90∘=g, directed vertically downwards


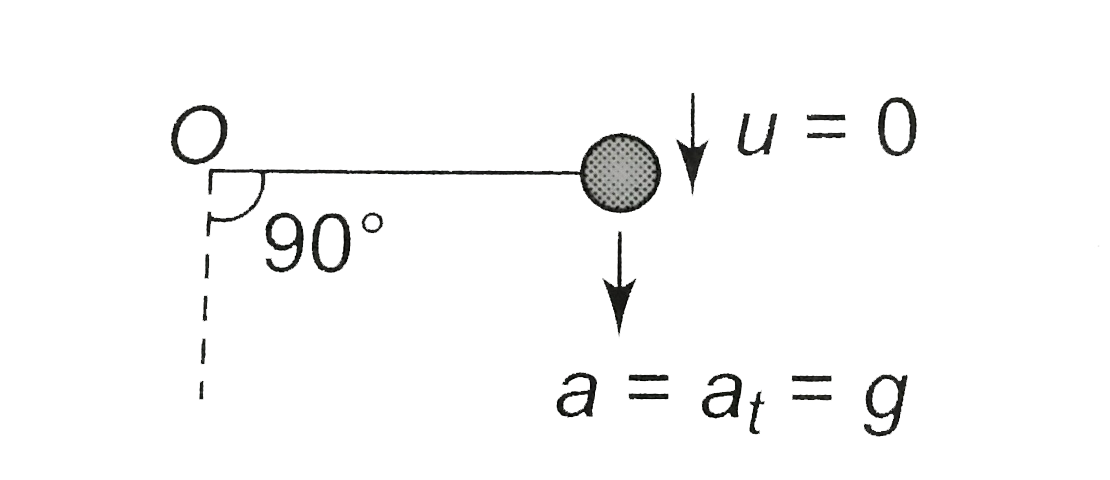
Topper's Solved these Questions
Similar Questions
A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.View SolutionA small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View Solution
Knowledge Check
- Question 1 - Select One or More
A small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg. - Question 2 - Select One
A small sphere of mass m is supended by a thread of length l. It is raised upto the height of suspension with thread fully stretched and released. Then, the maximum tension in thread will be
AmgB2 mgC3 mgD6 mg - Question 3 - Select One
If a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vectical charged conductinb plate, then for equilibrium of sphere the surface charge density of the plate -
Aε0mgtanθqB(2ε0mgtanθ)/qCε0mgqtanθDε0mgtanθ3q
A block of mass M lies on a plane inclined at an angle α to the horizontal. A wieght a mass m is connected to the block by a thread slung over a pulley (Fig.).
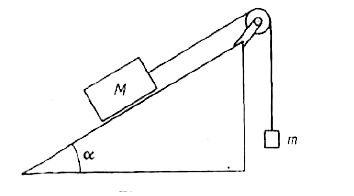
Find the acceleration of the weight and the tension of the thread. Friction, the mass of the pulley and of the thread are to be neglected.View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
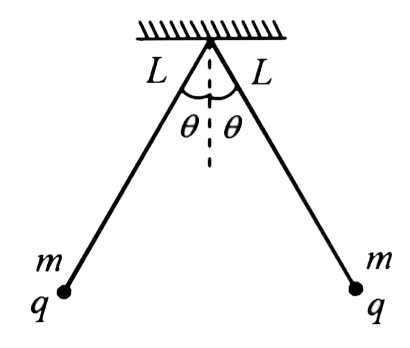 View Solution
View SolutionA weight of mass m hangs on a thread. The thread is deflected by an angle α0 and let go. Find the tension of the thread as a function of the angle α .
View SolutionIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
View SolutionIn shown figure, the trolley starts accelerating with acceleration a. The maximum angle deflected by thread from vertical will be:
 View Solution
View Solution

