A rifle was aimed at the vertical line on the target located precisely in the northern direction, and then fired. Assuming the air drag to be negligible, find how much off the line, and in what direction, will the bullet hit the target. The shot was fired in the horizontal direction at the latitude $φ = 60^{\circ}$ , the bullet velocity $v = 900 m / s$ , and the distance from the target equals $s = 1.0 k m$ .

Text Solution

Verified by Experts

Define the axes as shown with z along the local vertical, x due east and y due north. (We assume we are in the northern hemisphere). Then the Coriolis force has the componets.
${\to F}_{c or} = - 2 m (\to ω \times \to v)$
$= 2 m ω [v_{y} cos θ - v_{x} sin θ) \to i - v_{x} cos θ \to j + v_{x} cos θ \to k] = 2 m ω (v_{y} cos θ - v_{x} sin θ) \to i$
since $v_{x}$ is small when the direction in which the gun is fired is due north. Thus the equation of motion (neglecting centrifugal forces) are
$. . x = 2 m ω (v_{y} sin φ - v_{x} cos φ)$ , $. . y = 0$ and $. . z = - g$
Integrating we get $. y = v$ (constant), $. z = - g t$
and $. x = 2 ω v sin φ t + ω g t^{2} cos φ$
Finally,
$x = ω v t^{2} sin φ + \frac{1}{3} ω g t^{3} cos φ$
Now $v > > g t$ in the present case. so,
$x \approx ω v sin φ {(\frac{s}{v})}^{2} = ω sin φ \frac{s^{2}}{v}$
$\approx 7 c m$ (to the east).

Updated on:21/07/2023

A bullet fired from a rifle travels at an average speed of 2520 km/hr. It hits the target after 0.2 seconds. How far (in m) is the target from the rifle ?
A70
B140
C100
D200
A bullet is fired from a rifle that is held 1.6 m above the ground in a horizontal position. The initial speed of the bullet is 1100 m/s. Find the time it takes for the bullet to strike the ground and the horizontal distance traveled by the bullet.
A0.24 s, 693 m
B0.57 s, 630 m
C0.32 s, 440 m
D0.63 s, 352 m
A bullet with muzzle velocity $100 m s^{- 1}$ is to be shot at a target $30 m$ away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
.
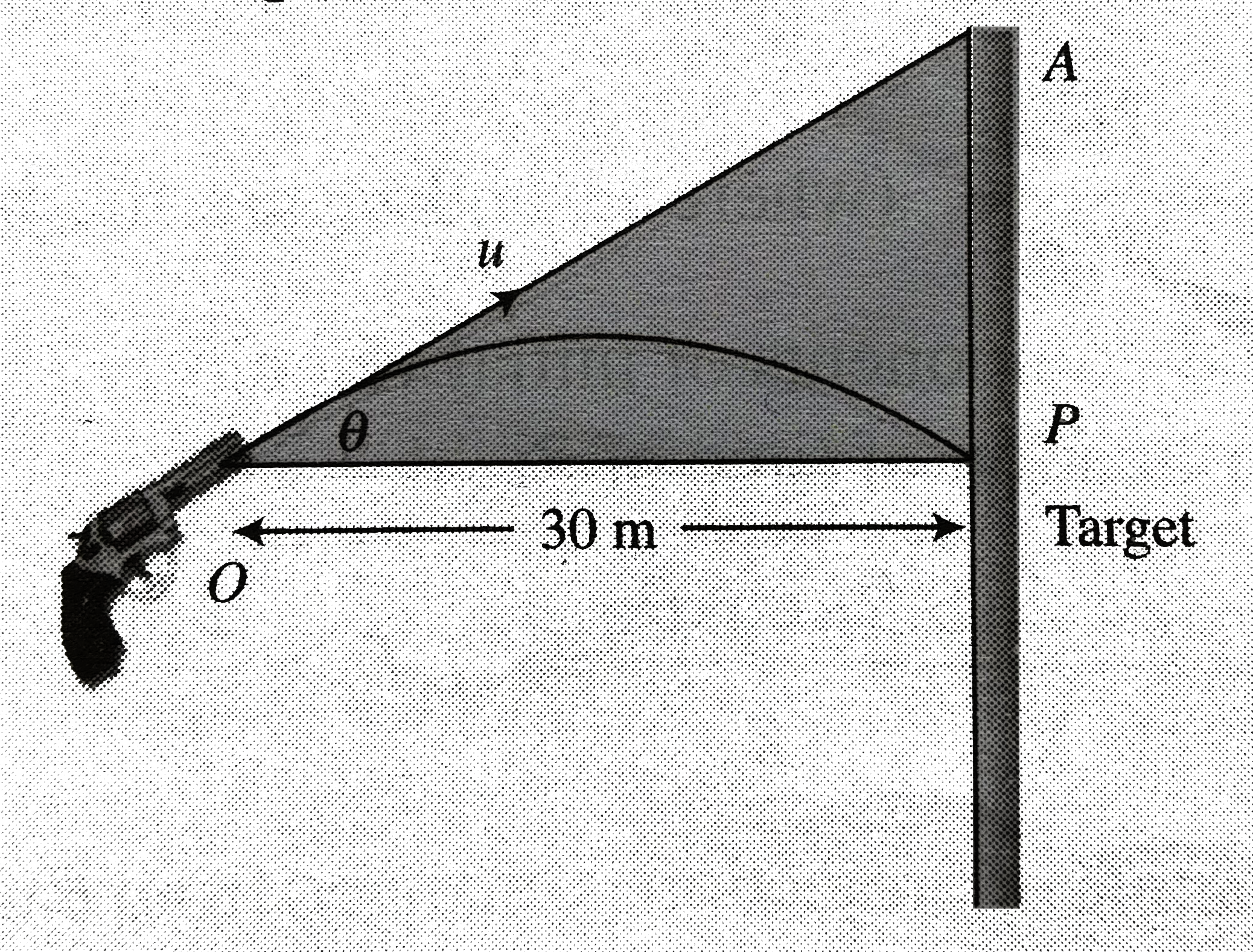A0
B0.45cm
C45cm
D90cm