A chain of mass and length rests on a rough-surfaced table so that one of its ends hangs over the edge. The chain starts sliding off the table all by itself provided the overhanging part equals of the chain length. What will be the total work performed by the friction forces acting on the chain by the moment it slides completely off the table?
To solve the problem, we need to analyze the situation step by step. The chain is resting on a rough table, with part of it hanging off the edge. When a certain portion of the chain (1/3 of its total length) hangs off the edge, it begins to slide off due to gravity. We need to calculate the total work done by the friction forces acting on the chain until it slides completely off the table.
1. Identify the parameters:
- Mass of the chain, m=0.80kg
- Length of the chain, l=1.5m
- Overhanging length, η=13l=13×1.5m=0.5m
2. Determine the mass of the overhanging part:
- The mass per unit length of the chain, λ=ml=0.80kg1.5m=815kg/m
- Mass of the overhanging part, moverhang=λ⋅η=815⋅0.5=415kg
3. Calculate the gravitational force acting on the overhanging part:
- The gravitational force, Fg=moverhang⋅g=415⋅9.81m/s2≈2.613N
4. Determine the frictional force acting on the chain:
- The frictional force Ff can be expressed as Ff=μ⋅N, where N is the normal force acting on the part of the chain that is still on the table.
- The normal force N=mremaining⋅g=(m−moverhang)⋅g=(0.80−415)⋅9.81
5. Calculate the work done by friction:
- The work done by the friction force as the chain slides off the table can be calculated using the formula W=Ff⋅d, where d is the distance the chain slides.
- The total distance d that the chain slides is equal to the length of the chain l=1.5m.
6. Combine the results to find the total work done:
- Substitute the values into the work done formula to find W.
Final Calculation:
1. Calculate N:
N=(0.80−415)⋅9.81≈(0.80−0.267)⋅9.81≈0.533⋅9.81≈5.23N
2. Calculate Ff:
Ff=μ⋅N
(Assuming a coefficient of friction μ is provided or can be assumed for rough surfaces.)
3. Calculate the work done:
W=Ff⋅d=Ff⋅1.5
- Mass of the chain, m=0.80kg
- Length of the chain, l=1.5m
- Overhanging length, η=13l=13×1.5m=0.5m
- The mass per unit length of the chain, λ=ml=0.80kg1.5m=815kg/m
- Mass of the overhanging part, moverhang=λ⋅η=815⋅0.5=415kg
- The gravitational force, Fg=moverhang⋅g=415⋅9.81m/s2≈2.613N
- The frictional force Ff can be expressed as Ff=μ⋅N, where N is the normal force acting on the part of the chain that is still on the table.
- The normal force N=mremaining⋅g=(m−moverhang)⋅g=(0.80−415)⋅9.81
- The work done by the friction force as the chain slides off the table can be calculated using the formula W=Ff⋅d, where d is the distance the chain slides.
- The total distance d that the chain slides is equal to the length of the chain l=1.5m.
- Substitute the values into the work done formula to find W.
1. Calculate N:
N=(0.80−415)⋅9.81≈(0.80−0.267)⋅9.81≈0.533⋅9.81≈5.23N
Ff=μ⋅N
(Assuming a coefficient of friction μ is provided or can be assumed for rough surfaces.)
W=Ff⋅d=Ff⋅1.5
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A chain of mass m and length l rests on a roung surfced table so that one of its ends hangs over the edge. The chain starts sliding off the table all by itself provided the overhanging part equals 1/3of the chain length. What will be the total work performed by the fricition forces acting on the chain by the moment is slides completely off the table ? Friction cofficient is μ
View SolutionA uniform chain of mass m0 and length l rests on a rough incline with its part hanging vertically as shown in the fig. The chain starts sliding up the incline (and hanging part moving down) provided the hanging part equals η times the chain length (η lt 1). What is the work performed by the friction force by the time chain slides completely off the incline. Neglect the dimension of pulley and assume it to be smooth.
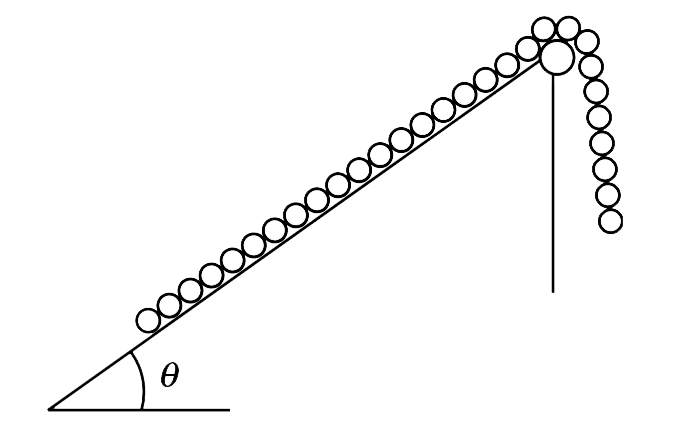 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36 - Question 2 - Select One
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36 - Question 3 - Select One
A uniform chain has a mass m and length l . It is held on a frictionless table with one - sixth of its length hanging over the edge. The work done in just pulling the hanging part back on the table is :
Amgl72Bmgl36Cmgl12Dmgl6
A chain of mass m and length 1 lies on a rough table. The chain just starts to slip when the overhaning part equals nth fraction of the chain length. If the chain is slightly distributed so that it completely slips off the table, what is the work performed by the friction forces.
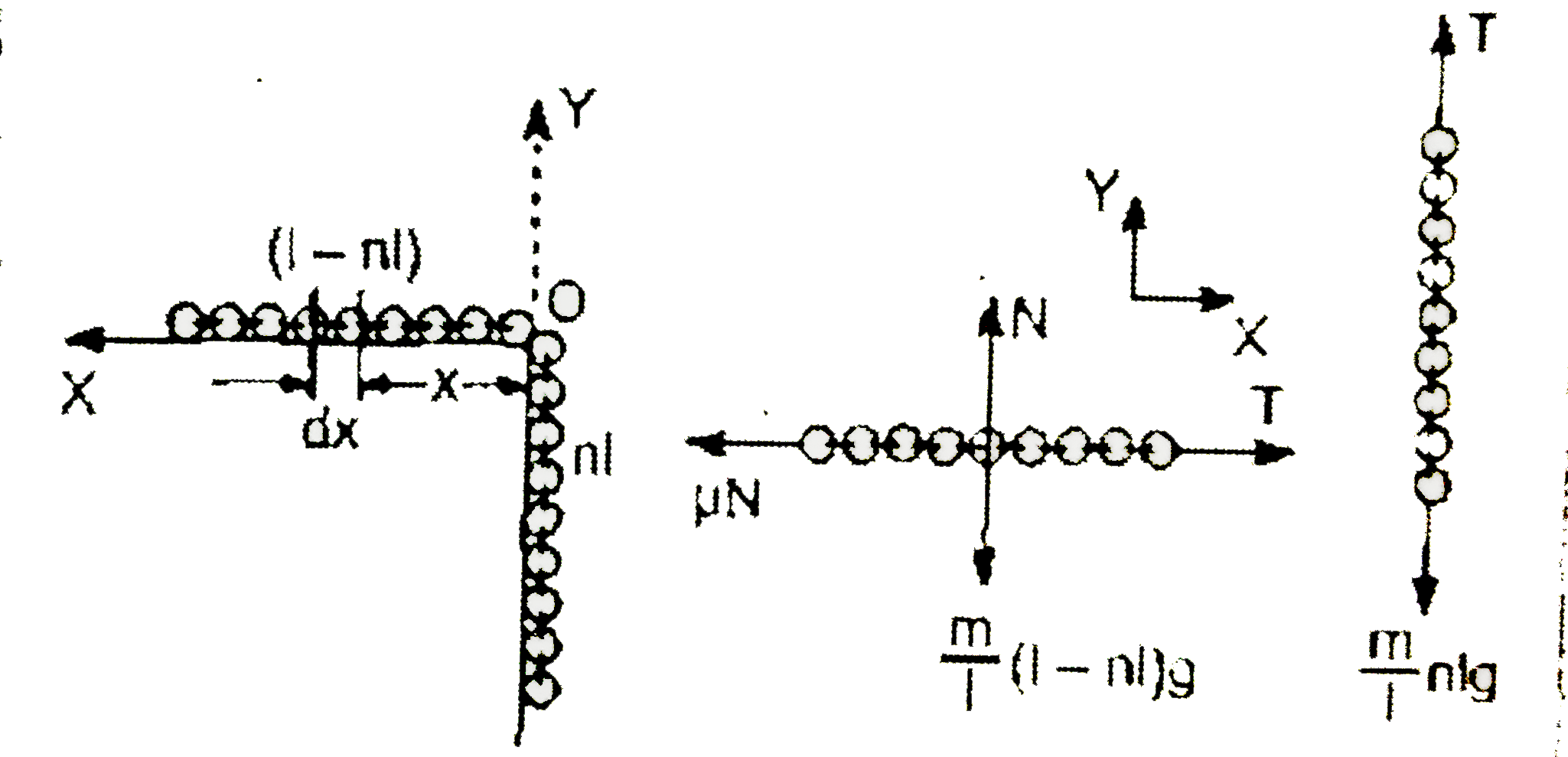 View Solution
View SolutionA chain of linear density 3 kg /m and length 8 m is lying on the table with 4 m of chain hanging from the edge. The work done in lifting the chain on the table will be -
View SolutionA uniform chain of length l is placed on a rough table, with length l/3 hanging over the edge. If the chain just begins to slide off the table by itself from this portion, the coefficient of friction between the chain and the table is 1/K. Then find the value of K.
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?View SolutionA uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View Solution

