A uniform solid cylinder of mass and radius is set in rotation about its axis with an angular velocity , then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to . Find
() how long the cylinder will move with sliding,
() the total work performed by the sliding friction force acting on the cylinder.
(a) Let us depict the forces acting on the cylinder and their point of applications for the cylinder and indicate positive direction of and as shown in the figure. From the equations for the plane motion of a solid and :
or (1)
or (2)
Let the cylinder starts pure rolling at after releasing on the horizontal floor at . From the angular kinematical equation.
,
or (3)
From the equation of the linear kinematics,
or (4)
But at the moment , when pure rolling starts
so,
Thus

(b) As the cylinder pick, up speed till it starts rolling, the point of contact has a purely translatory movement equal to in the forward directions but there is also a backward movment of the point of contant of magnitude . Because of slipping the net displacement is backwards. The total work done is then,
The same result can also be obtained by the work-energy theorem, .
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?
 View Solution
View SolutionA uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity ω0(=40√π rad s−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=2). Then, how many rotations will the cylinder make before it comes to rest?
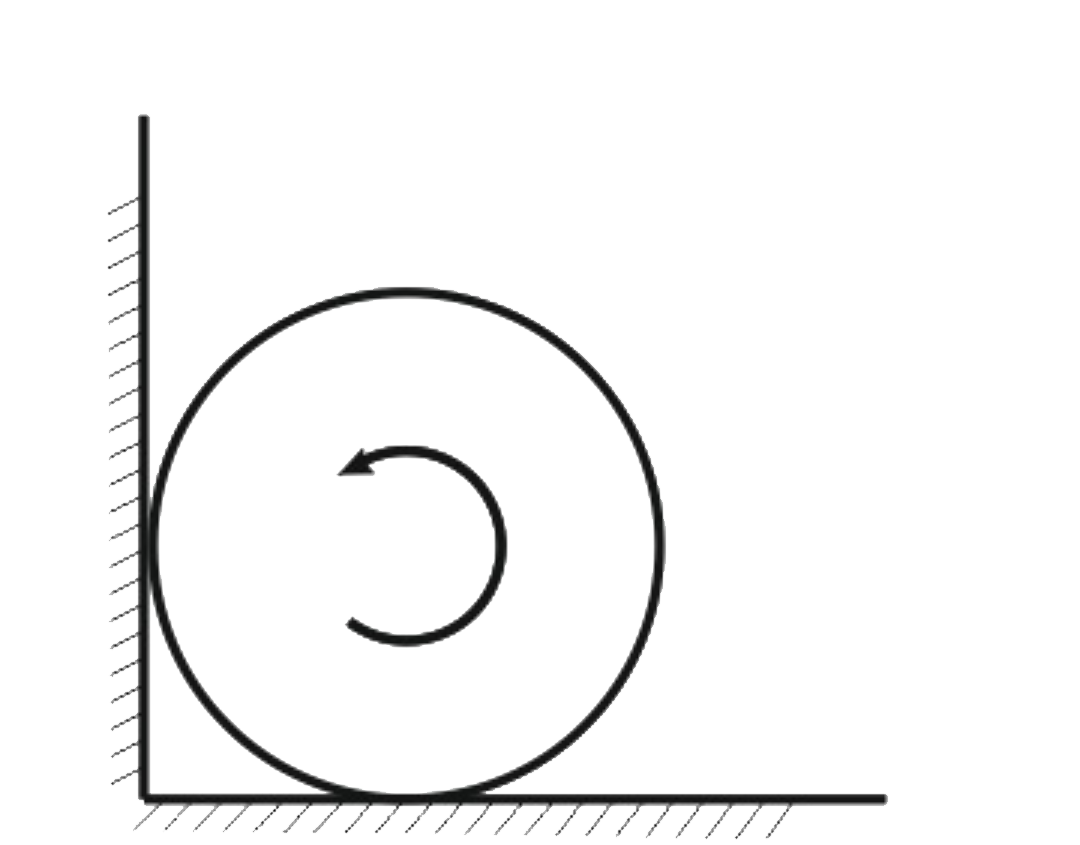 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2 - Question 2 - Select One
An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
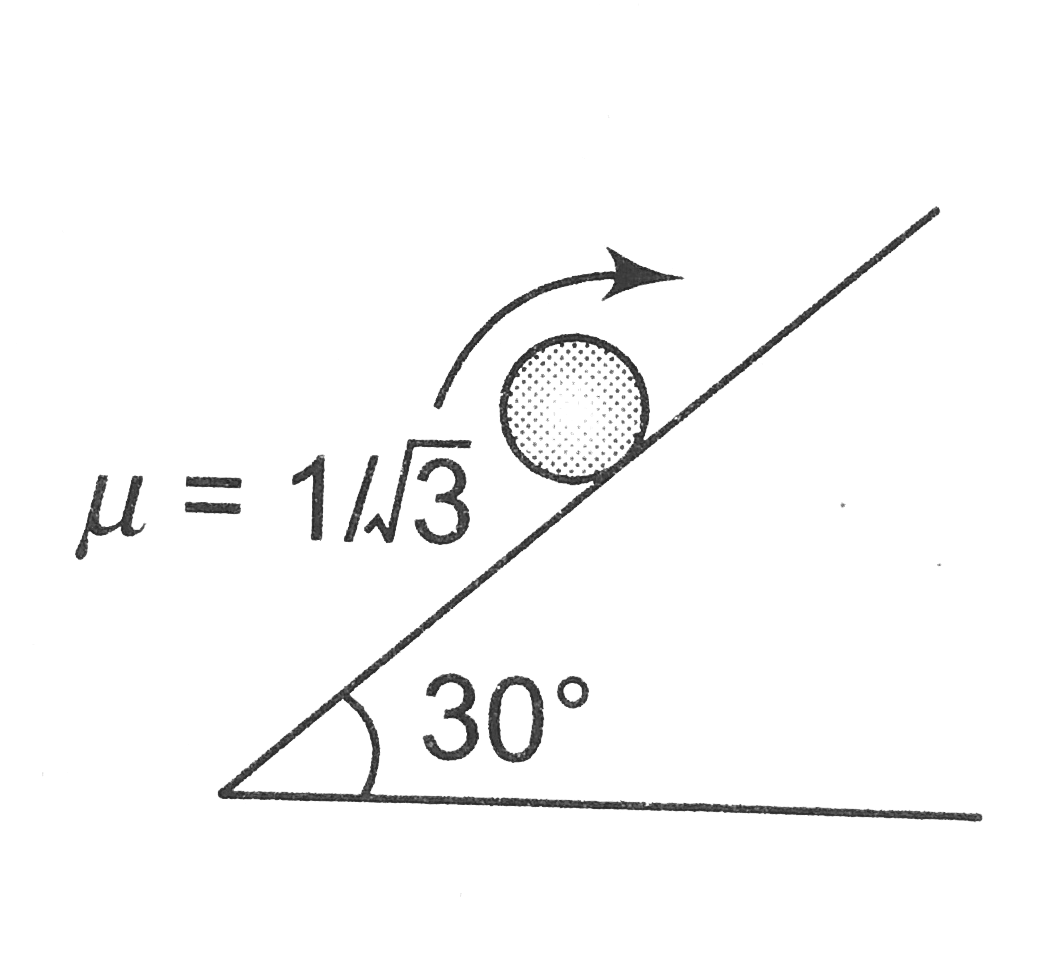 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward. - Question 3 - Select One
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
A cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View SolutionAn solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is.
View Solution
