Proceeding from the fundamental equation of relativistic dynamics, find:
(a) under what circumstances the acceleration of a particle coincides in direction with the force F acting on ti,
(b) the proportionality factors relating the force F and the acceleration w in the cases when F⊥v and F∣∣v, where v is the velocity of the particle.
→F=ddt⎛⎜
⎜⎝m0→v√1−v2c2⎞⎟
⎟⎠=m0→v√1−v2c2+m0→vc2→v⋅→v1(1−v2c2)3/2
Thus →F⊥=m0→w√1−β2,→w=→v,→w⊥→v
→F∣∣=m0→w(1−β2)3/2,→w=→v,→w∣∣→v
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
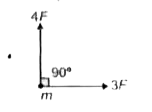
View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View Solution
Knowledge Check
When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
 AaB2aC5aD8a
AaB2aC5aD8aForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
A√ktmB√2ktmC2√ktmDnone of theseA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
A√km+v2B√2Wm+v2C√2Wk+v2D√W2m+v2
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particles of mass m moving in a circle of radius r with unform speed v. The force F acting on a particle is proportional ot mavbrc. Find the values of a, b and c.
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
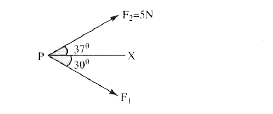
View SolutionIf v is the velocity and f is the acceleration of a particle, at time t, such that t=v22, then : −dfdt=
View Solution
