Find the rate v with which helium flows out of a thermally insulated vessel into vacuum through a small hole. The flow rate of the gas inside the vessel is assumed to be negligible under these conditions. The temperature of helium in the vessel is T=1.000K.
From energy conservation as in the derivation of Bernoullis theorem it reads
pρ+12v2+gz+u+Qd=constant ….(1)
In the Eq.(1) u is the internal energy per unit mass and in this case is the thermal energy per unit mass of the gas. As the gas vessel is thermally insulated Qd=0, also in our case.
Just inside the vessel u=CVTM=RTM(γ−1)alsopρ=RTM. inside the vessel v=0 also. Just outside p=0, and u=0. Ingeneral gz is not very significant for gases.
Thus applying Eq. (1) just inside and outside the hole, we get
12v2=pρ+u
=RTM+RTM(γ−1)=γaRTM(γ−1)
Hence v2=2γRTM(γ−1) or, v=√2γRTM(γ−1)=3.22km/s.
The velocity here is the velocity of hydrodynamic flow of the gas into vaccum.This requires that the diameter of the hole is not too small (D> mean free l). In the opposite case (D<<l) the flow is called effusion. Then the above result does not apply and kinetic theory methods are needed.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases51videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy47videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
A thermally insulated vessel containing a gas, whose molar mas is equal to M and specific heat capacity ratio γ, moves with a velocity V. Find the temperature rise when the vessel is stopped suddenly.
View SolutionThree insulated vessels of equal volumes V are connected by thin tubes that can transfer gas but do not transfer heat. Initially all the vessels are filled with the same type of gas at a temperature T0 and pressure P0. Then the temperature in the first vessel is doubled and the temperature in the second vessel is tripled. The temperature in the thin vessel remains unchanged. If initial pressure is 77cm of Hg, then find the final pressure (in cm of Hg ) in the system.
View Solution
Knowledge Check
- Question 1 - Select One or More
A thermally insulated vessel containing diatomic gas of molar mass M is moving with velocity v. the temperature of gas is T. if it is suddenly stopped, then
AInternal energy of gas is equal to 5nRT2 when vessel is movingBThere is no change in temperature if vessel is suddenly stoppedCThere is rise in temperature if vessel is suddenly stoppedDTemperature increase is due to heat input - Question 2 - Select One
A certain gas effuses through a small opening of a vessel at a rate which is exactly one-fifth the rate at which helium does the same. Thus, the molecular weight of the gas is :
A100B75C50D25 - Question 3 - Select One
Two thermally insulated vessel 1 and 2 are filled with air at temperature (T1T2),volume(V1V2) and pressure (P1P2) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
AT1T2(P1V1+P2V2)/(P1V1T2+P2V2T1)B(T1+T2)/2CT1+T2DT1T2(P1V1+P2V2)/(P1V1T1+P2V2T2)
Two vessels A and B of equal volume (V0) are connected by a narrow tube which can be closed by a value. The vessels are fitted with piston which can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (CpCv=γ) at atomspheric pressures(P0) and atmoshpeheric temperature (T0). The walls of the vessels A are diathermic and those of B are adiabatic. The value is now closed and the pistons are slowly pulled out to increase the volumes of the of the vessels to dobuled the original value.(a) Find the temperatures and pressures in the two vessels. (b) The value is now opened for sufficeint time so that the gases acquire a common tempertures and pressures . Find the new values of the temperatuere and the pressures.
View SolutionA vessel containing one gram -mole of oxygen is enclosed in a thermally insulated vessel. The vessel is next moved with a constant speed v0 and then suddenly stopped. The process results in a rise in the temperature of the gas by 1∘c. Calculate the speed v0.
View SolutionTwo adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
View SolutionIn the figure shown, water flows into the open vessel through pipe A at a constant rate. The water can flow out of the vessel by pipe B. The maximum flow-rate fo the water in pipe B is slightly more than that in pipe A. Final height of the water level in the vessel would be
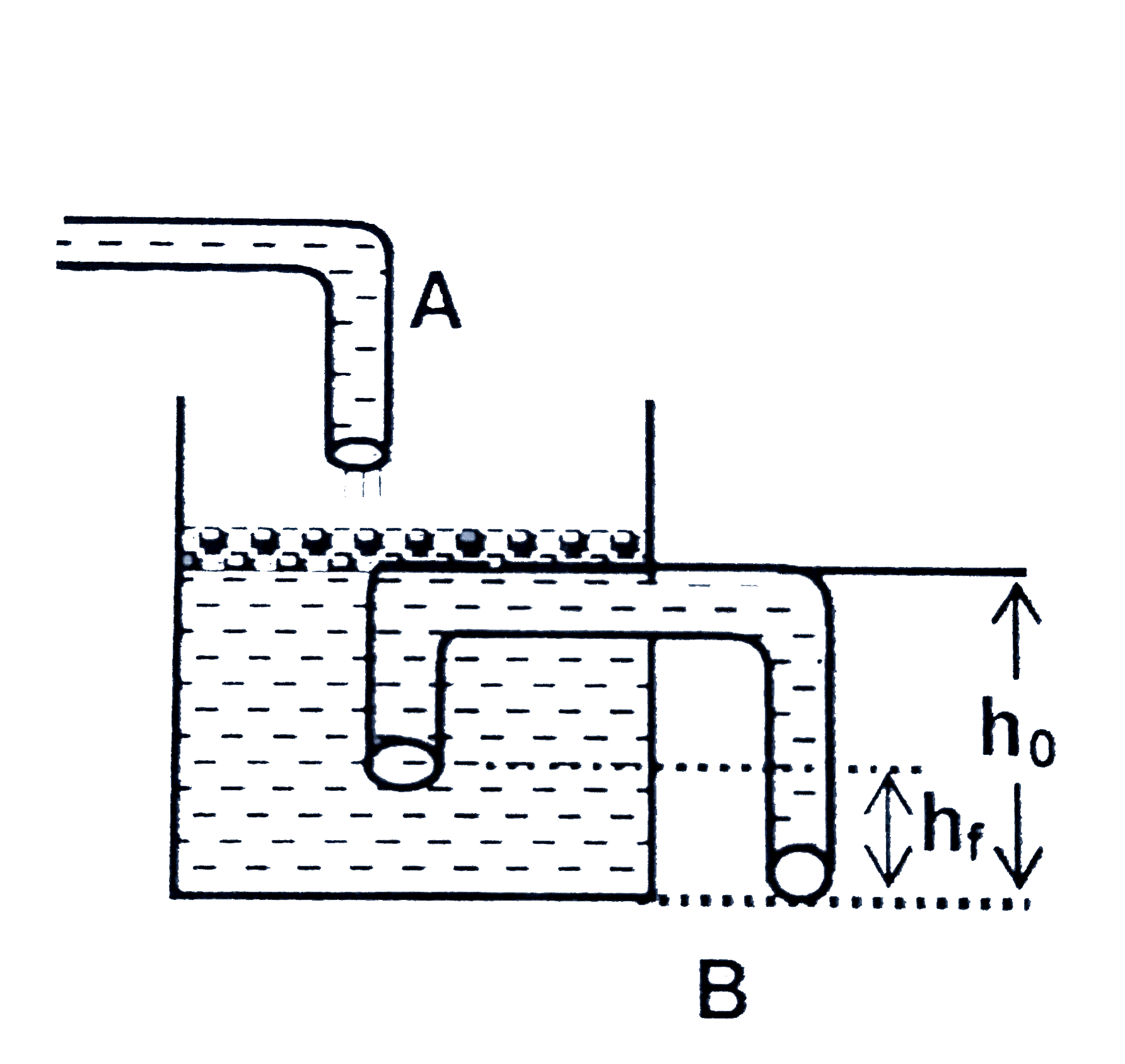 View Solution
View SolutionA 4:1 mixture of helium and methane contained in a vessel at 10 bar pressure. During a hole in the vessel, the gas mixture leaks out. The composition of the mixture effusing out initially is
View Solution

