Find the temperature distribution in a substance palced between two pa

The efficiency of an ideal heat engine working between the temperature $T_{1}$ and $T_{2} (T_{1} > T_{2})$ is
A $1 - \frac{T_{1}}{T_{2}}$
B $1 - \frac{T_{2}}{T_{1}}$
C $1 + \frac{T_{2}}{T_{1}}$
D $\frac{T_{2}}{T_{1}}$
$χ_{1}$ and $χ_{2}$ are susceptinilities of diamagnetic substance at temperatures $T_{1} K$ and $T_{2} K$ respectively. Then
A $χ_{1} T_{1} = χ_{2} T_{2}$
B $χ_{1} = χ_{2}$
C $χ_{1} \sqrt{T_{1}} = χ_{2} \sqrt{T_{2}}$
D $χ_{1} T_{2} = χ_{2} T_{1}$
The figure shows a system of two concentric spheres of radii $r_{1} and r_{2}$ are kept at temperature $T_{1} and T_{2}$ , respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

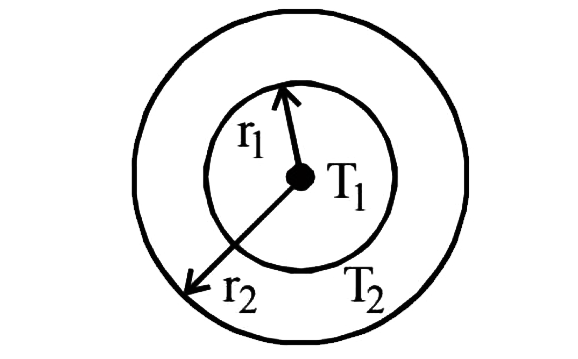A $I n (\frac{r_{2}}{r_{1}})$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}}$
C $(r_{1} - r_{2})$
D $\frac{r_{1} r_{2}}{r_{2} - r_{1}}$

Find the temperature distribution in a substance palced between two parallel plates kept at temperatures $T_{1}$ and $T_{2}$ . The plate separation is equal to $l$ , the heat conductivity coefficient of the substance $x ¯ ¯¯¯¯ ¯ \propto V ¯ ¯ ¯ T$ .