Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
The arrangment of the rings are as shwon in Figure. Now, potential at the point 1, φ1 = potential at 1 due to the ring 1+ potential at 1 due to the ring 2.
=q4πε0R+−q4πε0(R2+a2)1/2
Similarly, the potential at point 2,
φ2=−q4πε0R+q4πε0(R2+a2)1/2
Hence, the sought potentail differnce,
φ1−φ2=Δφ=2(q4πε0R+−q4πε0(R2+a2)1/2)
=q2πε0R⎛⎜
⎜⎝1−1√1+(a/R)2⎞⎟
⎟⎠

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Knowledge Check
Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
A(a) q2π∈0[1R−1√R2−d2]B(b) qR4π∈0d2C(c) q4π∈0[1R−1√R2+d2]D(d) zeroA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R>r0. The potential difference between the two is
AProportional to QBProportional to qCDependent on both Q and qDIndependent of both Q and qA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
Aproportional to QBProportional to qCDependent on both Q and qDindependent of both Q and q
Two identical thin rings, each of radius R, are coaxially placed a distance R apart. Q1 and Q2 are respectively the charges uniformly spread on the two rings. The work done in moving a charge q fróm the centre of one ring to that of the other is (√x−y)q(Q2−Q1)4√2πɛ0R. Find (x−y)
View SolutionA ring of radius R carries a charge q uniformly distribited over it. A long thin wire carrying charge λper unit length of it is held along its axis with one end coinciding with the centre of the ring. Find the interaction force between the ring and the thread.
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
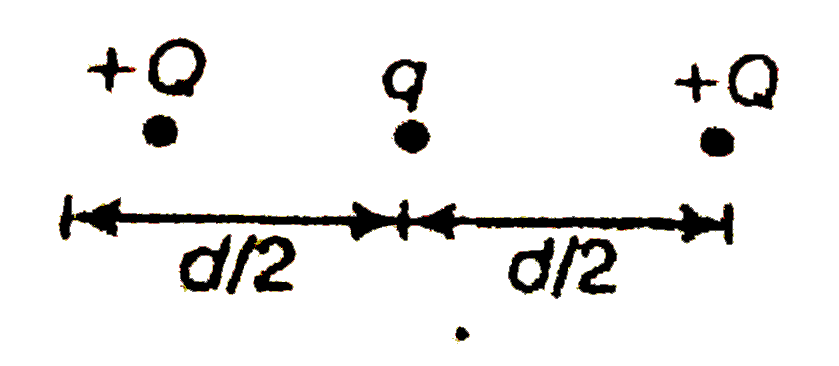
View SolutionTwo positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
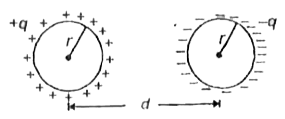
View SolutionTwo similar conducting balls having charges + q and - q are placed at a separation d from each other in air. The radius of each ball is r and the separation between their centres is d (d >> r ). Calculate the capacitance of the two ball system
View Solution
