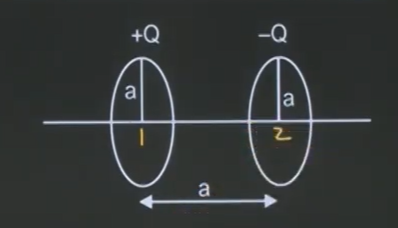
The two oppositely charged rings of radii a are seprated by s . Find the potential difference between center of the ring ?
To find the potential difference between the centers of two oppositely charged rings of radius a separated by a distance s, we can follow these steps:
1. Define the Setup:
- Let the first ring (Ring 1) have a positive charge +Q and the second ring (Ring 2) have a negative charge −Q.
- The distance between the centers of the two rings is s.
2. Potential at the Center of Ring 1:
- The potential V1 at the center of Ring 1 (which is at a distance 0 from itself) due to its own charge is given by the formula:
V1=kQa
- Here, k is Coulomb's constant (k=14πϵ0).
3. Potential at the Center of Ring 1 due to Ring 2:
- The potential V1,2 at the center of Ring 1 due to Ring 2 (which is at a distance s from Ring 1) is given by:
V1,2=k−Q√s2+a2
- This is because the center of Ring 2 is at a distance s from the center of Ring 1, and we include the negative sign for the negative charge.
4. Total Potential at the Center of Ring 1:
- The total potential V1 at the center of Ring 1 is:
V1=kQa+k−Q√s2+a2=kQ(1a−1√s2+a2)
5. Potential at the Center of Ring 2:
- The potential V2 at the center of Ring 2 due to its own charge is:
V2=k−Qa
- The potential V2,1 at the center of Ring 2 due to Ring 1 (which is at a distance s) is:
V2,1=kQ√s2+a2
6. Total Potential at the Center of Ring 2:
- The total potential V2 at the center of Ring 2 is:
V2=k−Qa+kQ√s2+a2=kQ(−1a+1√s2+a2)
7. Potential Difference:
- The potential difference V between the centers of the two rings is given by:
V=V1−V2
- Substituting the expressions for V1 and V2:
V=kQ(1a−1√s2+a2)−kQ(−1a+1√s2+a2)
- Simplifying this gives:
V=kQ(2a−2√s2+a2)=2kQ(1a−1√s2+a2)
Final Expression for Potential Difference:
V=2kQ(1a−1√s2+a2)
- Let the first ring (Ring 1) have a positive charge +Q and the second ring (Ring 2) have a negative charge −Q.
- The distance between the centers of the two rings is s.
- The potential V1 at the center of Ring 1 (which is at a distance 0 from itself) due to its own charge is given by the formula:
V1=kQa
- Here, k is Coulomb's constant (k=14πϵ0).
- The potential V1,2 at the center of Ring 1 due to Ring 2 (which is at a distance s from Ring 1) is given by:
V1,2=k−Q√s2+a2
- This is because the center of Ring 2 is at a distance s from the center of Ring 1, and we include the negative sign for the negative charge.
- The total potential V1 at the center of Ring 1 is:
V1=kQa+k−Q√s2+a2=kQ(1a−1√s2+a2)
- The potential V2 at the center of Ring 2 due to its own charge is:
V2=k−Qa
- The potential V2,1 at the center of Ring 2 due to Ring 1 (which is at a distance s) is:
V2,1=kQ√s2+a2
- The total potential V2 at the center of Ring 2 is:
V2=k−Qa+kQ√s2+a2=kQ(−1a+1√s2+a2)
- The potential difference V between the centers of the two rings is given by:
V=V1−V2
- Substituting the expressions for V1 and V2:
V=kQ(1a−1√s2+a2)−kQ(−1a+1√s2+a2)
- Simplifying this gives:
V=kQ(2a−2√s2+a2)=2kQ(1a−1√s2+a2)
V=2kQ(1a−1√s2+a2)
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
A(a) q2π∈0[1R−1√R2−d2]B(b) qR4π∈0d2C(c) q4π∈0[1R−1√R2+d2]D(d) zeroTwo circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
A60KVB81KVC43KVD71KVTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
AzeroBQ4πε0[1R−1√R2+d2]CQ4πε0d2)DQ2πε0[1R−1√R2+d2]
Two rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
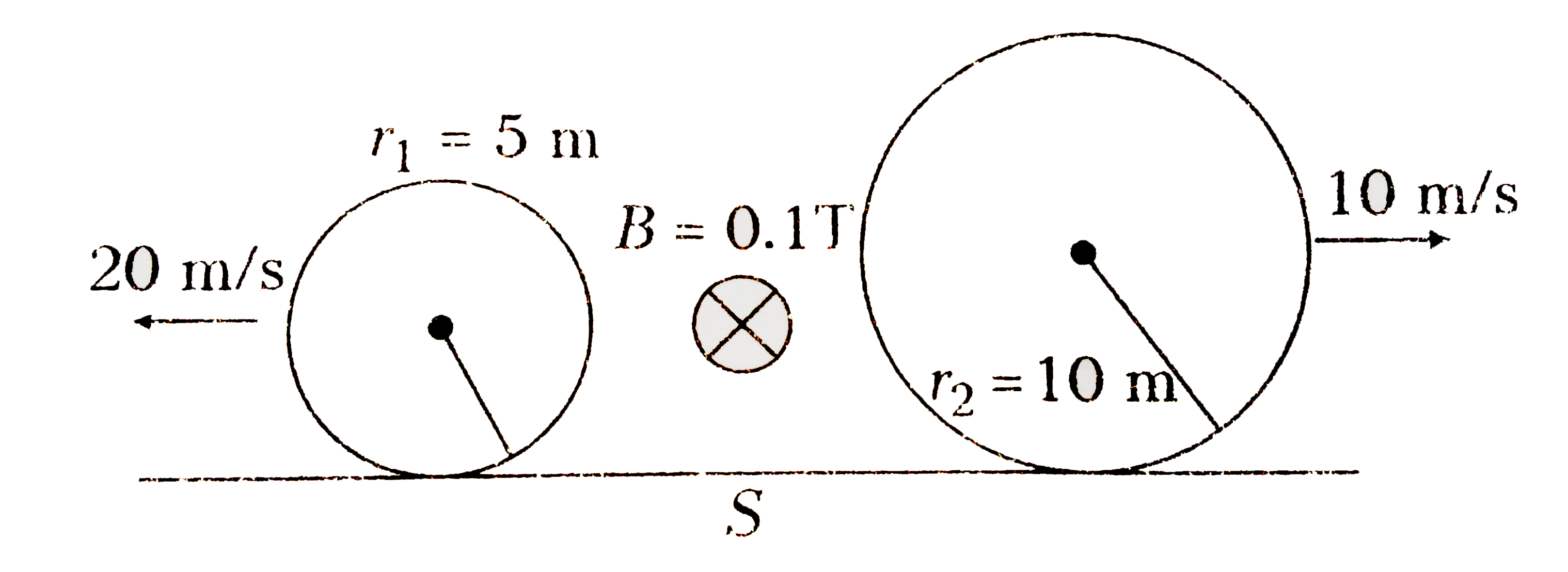
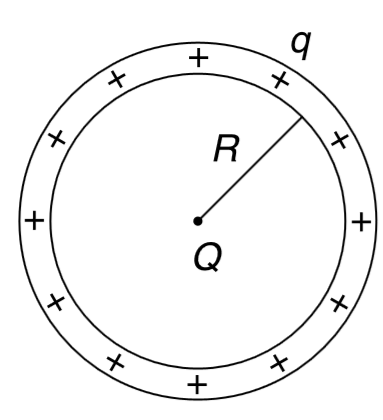
View SolutionA ring of radius R has uniformly distributed charge q. A point charge Q is placed at the centre of the ring. (a) Find the increase in tension in the ring after the point charge is placed at its centre. (b) Find the increase in force between the two semicircular parts of the ring after the point charge is placed at the centre. (c) Using the result found in part (b) find the force that the point charge exerts on one half of the ring.
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionTwo identical conducing ring A and B of radius R are in pure rolling over a horizontal conducing plane with same speed (of center of mass) v but in opposite direction. A constant magnetic field B is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is:
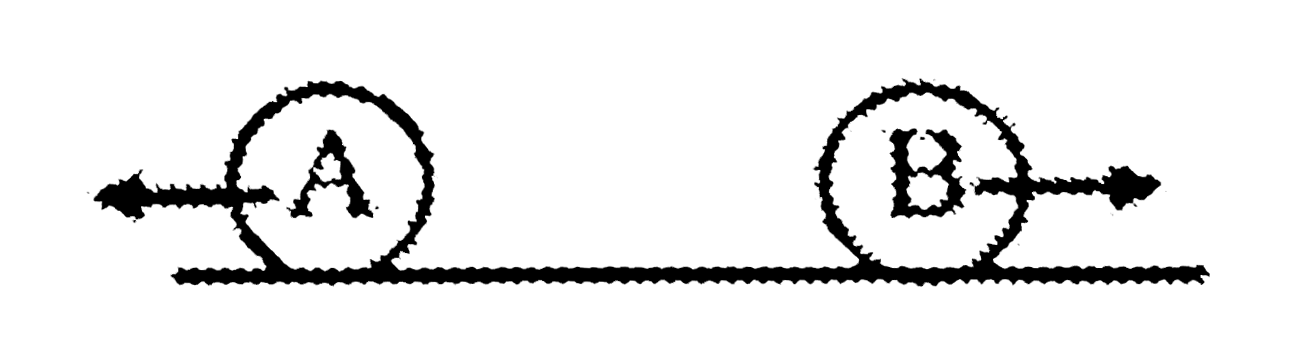
View SolutionTwo identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is

View Solution