A uniform istropic dielectric si shaped as a spherical layer with radii $a$ and $b$ . Draw the approximate plots of the electric field strength $E$ and the potential $φ$ vs the distance $r$ from the centre fo the layer if the dielectric has a certain positive extraneous charge distributed uniformly,
(a) over the internal surface of the layer, (b) over the volume of the layer.

Video Solution

Text Solution

Verified by Experts

(a) Positive extraneous charge is distributed uniformly over the internal surface layer. Let $σ_{0}$ be the surface density of the charge.
Clearlty $E = 0$ , for $r < a$
For $a < r$
$ε_{0} E \times 4 π r^{2} = 4 π a^{2} σ_{0}$ by Gauss theorem.
or, $E = \frac{σ_{0}}{ε_{0}} {(\frac{a}{r})}^{2}, a < r < b$
For $r > b$ , similarly
$E = \frac{σ_{0}}{ε_{0}} {(\frac{a}{r})}^{2}, r > b$
Now, $E = - \frac{\partial φ}{\partial r}$ ,
So by intergation from intensity where $φ (\infty) = 0$ ,
$φ = \frac{σ_{0} a^{2}}{ε_{0} r} r > b$

$a < r < b φ = \frac{σ_{0} a^{2}}{ε ε r} + B, B$ is a constant
or by continuity, $φ = \frac{σ_{0} a^{2}}{ε_{0} ε} (\frac{1}{r} - \frac{1}{b}) + \frac{σ_{0} a^{2}}{ε_{0} b}$
Positive extreneous charge si distributed uniformly over the internal volume of the dielectric
Let $ρ_{0}$ = volume density of the charge in the dielectric, for $a < r < b$ .
$E = 0, r < a$
$ε_{0} ε 4 π r^{2} E = \frac{4 π}{3} (r^{3} - a^{3}) ρ_{0}, (a < r < b)$
or, $E = \frac{ρ_{0}}{3 ε_{0}} (r - \frac{a^{3}}{r^{2}})$
$E = \frac{4 π}{3} (b^{3} - a^{2}) ρ_{0} / ε_{0} 4 π r^{2}, r > b$
or, $E = \frac{(b^{2} - a^{2}) ρ_{0}}{3 ε_{0} r^{2}}$ for $r > b$
By intergration,
$φ = \frac{(b^{2} - a^{3}) ρ_{0}}{3 ε_{0} r}$ for $r > b$
or, $φ = B = \frac{ρ_{0}}{3 ε_{0} ε} (\frac{r^{2}}{2} + \frac{a^{2}}{r}), a < r < b$
By continuity
$\frac{b^{3} - a^{3}}{3 ε_{0} b} ρ_{0} = B - \frac{ρ_{0}}{3 ε_{0} ε} (\frac{b^{2}}{2} + \frac{a^{3}}{b})$
or, $B = \frac{ρ_{0}}{3 ε_{0} ε} {\frac{ε (b^{2} - a^{2})}{b} + (\frac{b^{2}}{2} + \frac{a^{3}}{b})}$
Finally $φ = B - \frac{ρ_{0}}{3 ε_{0} ε} (\frac{a^{2}}{2} + a^{2}) = B - \frac{ρ_{0} a^{2}}{2 ε_{0} ε}, r < a$
On the basic of obtained expressions $E (r)$ and $(φ) (r)$ can be plotted as shown in the answer-sheet.

Updated on:21/07/2023

A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field $\to E$ at the centre O is

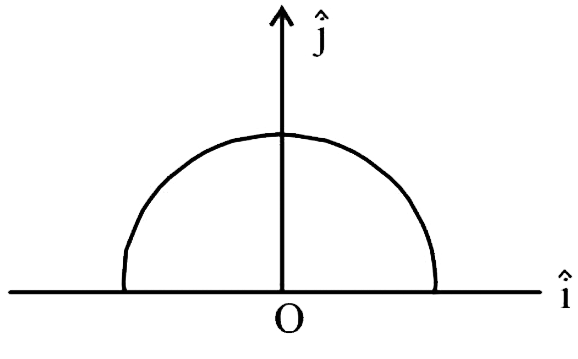A(a) $\frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
B(b) $- \frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
C(c) $- \frac{q}{2 π^{2} ε_{0} r^{20} ˆ j}$
D(d) $\frac{q}{2 π^{2} ε_{0} r^{2}} ˆ j$
A circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as

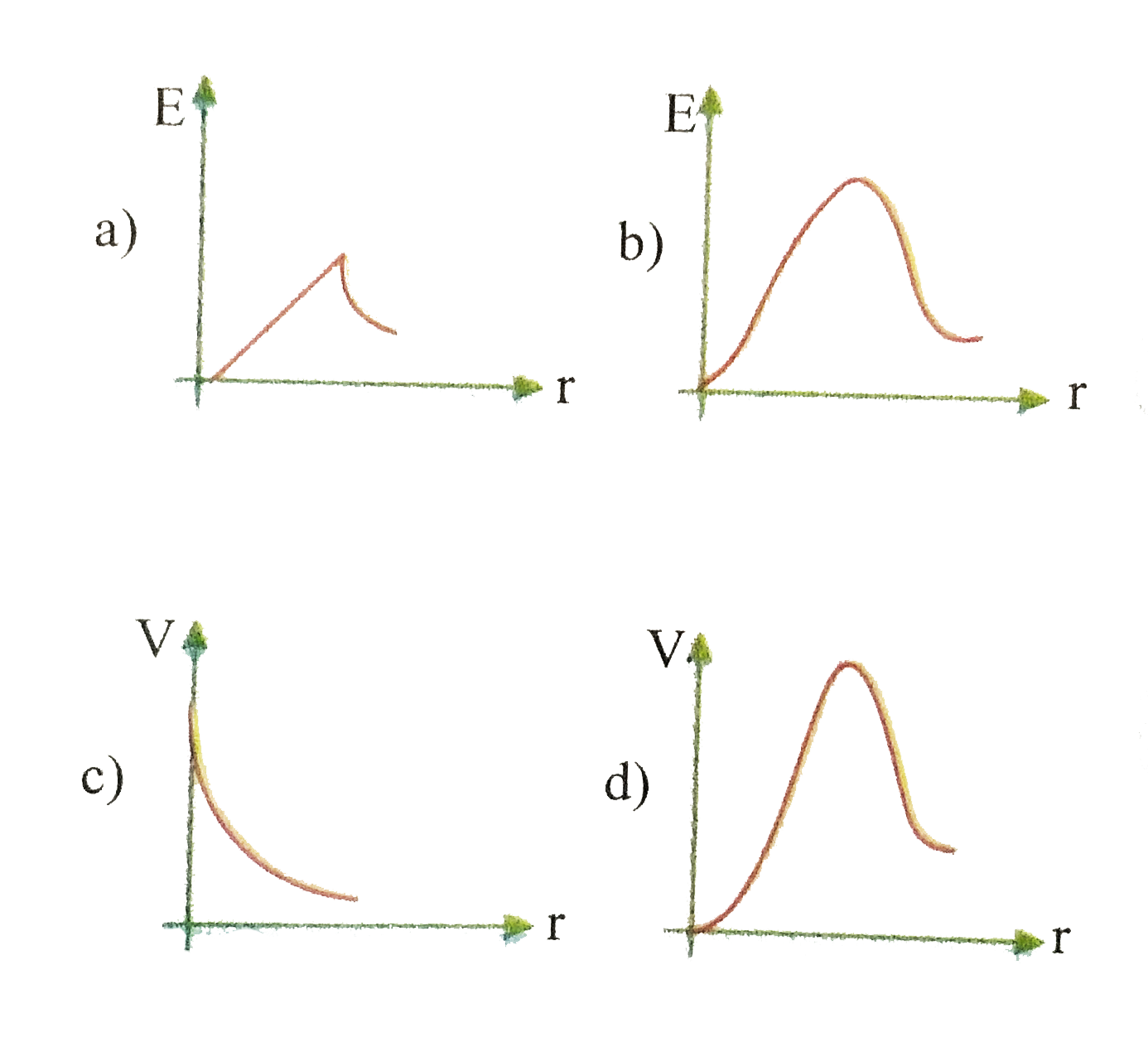A $b$ and $c$ are true
B $a$ is true
C $a, b, c$ are true
D $a, b, c, d$ are true
A spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
Ainside is zero and varies as $x^{- 1}$ outside it
Binside is non zero constant and varies as $x^{2}$ outside it
Cinside is zero and varies as $x^{- 2}$ outside it
Dinside is constant and varies as $x^{- 1}$ outside it