Find the potential due to an infinite sheet of charge at a distance x from it. Assume that the potential is zero at a distance a from it.
Although the infinite sheet can be treated as the special case of a disk, yet there are points that need be discussed. Let us do this by the formula we derived (Eq. 23-19), because the electric field of an infinite disk is known and is simple to handle.
Here we can use the formula we found before
ΔV=−∫→E.d→x=−∫xaσ2ε0.dx.
Here, we have assumed the potential to be zero at a distance of a from the sheet.
Vx=σ(a−x)2ε0.
We can note here that we cannot take the potential to be zero at infinity. If we do so, the potential will be infinite. This is because the electric field is also extending to infinity.
We can also note that a is just a arbitrary number we chose according to our convenience. It can have any fixed value and still it will not affect our calculations because in any situation, we want to find the change in potential energy. For that, we need to find only the change in potential. It will be the same for every value of constant a.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.13 Potential at the surface of the outer shell
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.14 Field and potential inside a charged spherical shell
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.11 Finding potential of charged disk
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
Both question (33) and (34) refer to the system of charges as shown in the figure. A spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting material. A point charge +Q is placed at the centre of the spherical shell and a total charge -q is placed on the shell.
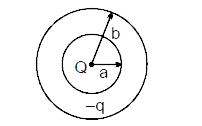
Assume that the electrostatic potential is zero at an infinite distance from the spherical shell. The electrostatic potential at a distance R(a<R<b) from the centre of the shell is
View SolutionA large metallic plate is facing a charged sheet having charge density σ placed parallel to plate at a distance l from the plate.Potential at point P at a distance x from the sheet is
View Solution
Knowledge Check
In the previous question assume that the electrostatic potential is zero at an infinite distance from the spherical shell. The electrostatic potential at a distance R(a<R<b) from the centre of the shell is where (K=14πε0)
A0BKQaCKQ−qRDKQ−qbBoth question a and b refer to the sustem of charges as shown in the figure. A spherical shell of conducting material. A point charge +Q is place at the centre of the spherical shell and a total charge −q is placed on the shell. A Charge −q id distributed on the surfaces as
 .
.
(b) Assume that the elctrostatic potential is zero at an infinite distance from the spherical shell . The electrostatic potential at a distance R(a<R<b) from the centre of the shell is .A0BKQaCKQ−qRDKQ−qb(w≠reK=14πɛ0)The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
The electric potential at surface of thin non-conducting sheet with charge density σ is V0. Show that the electric potential at a distance x from infinite sheet can be written as
V=V0−σ2∈0x
View SolutionTwo point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View SolutionTwo point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View SolutionA large metallic plate is facing a charged sheet having charge density "sigma" placed parallel to plate at a distance "l" from the plate.Potential at "point "P" at a distance [x" from the sheet is "]
View SolutionThe ratio of energy density in electric field (UE) to square of potential (V2) at point 'A' at a distance 'x' from static point charge Q is 'n'.The value of this ratio at a distance '3xfrom the charge is..?
View Solution
