A cylindrical capacitor is filled with two cyclindrical layers of dielectric with permittivity esπlon1 and esπlon2. The inside radii of the layers are equal to R1 and R2>R1. The maximum permissible values of electric field strength reaching teh breakdown value for both dielectrics simulttaneously ?
Let λ be the linear charge density then,
E1m=λ2πε0R1ε1 ….(1)
and E2m=λ2πε0R2ε2 ….(2)
The breakdown in either case will occur at the smaller value of r for a simulataneous breakdown of both dielectrics.
From (1) and (2) ltbr> E1mR1ε1=E2mR2ε2, which is the sougth relationship.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A double-layer cylindrical capacitor consists of conductors of radii R1 and R3 and two layers of dielectrics of relative permittivtties ε1 and esπon2. The radius of the common surface of the dielectrics. Is R2 . The breakdown field strengths of the dielectrics are E1 and E2 respectively. What is the breakdown voltage of this capacitor if (a) ε1R1E1<ε2R2E2 (b)ε2R2E2>ε1E1R1?
[Hint: If E1=E1max and E2>,E2max dielectric 1 will break first and if E2=E2max'E1>E1max dielectric 2 will break first.]
View SolutionFind the capacitance of an isolated ball-shaped conductor of radius R1 surrounded by an adjacent concentric layer of dielectric with permittivity ε and outside radius R2.
View Solution
Knowledge Check
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0dThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
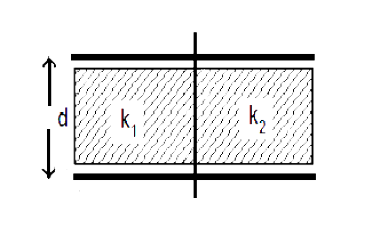 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
The gap between the plates of a prallel-plate capacitor is filled up with two dielectric layers 1 and 2 thickness d1 and d2 permittivities ε1 and ε2 and resistivities ρ1 and ρ2. A dc voltage V is applied to the capacitor with electric field directed from layer 1 to layer 2 find σ the surface density of extraneous charges at the boundary between the dielectric layers and the condition under with σ=0.
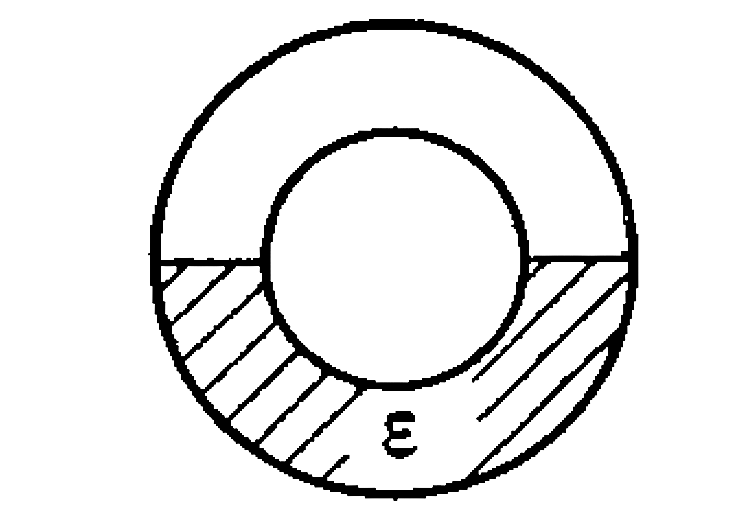
View SolutionHalf the space between two concentricv elecrodes of a sphereical capacitor is filled , as shwon in Fig, with unifrom istropic dielectric with permittively ε. The charge of the capacitor is q. Find the magnitude of the electric field strength between teh electrodes as a function of distance r from the curvature centre of teh electrodes.
View SolutionThe space between the plates of a parallel-plate capacitor is filled consecutively with two dielectric layers 1 and 2 having the thickness of d1 and d2 and the permittivities esπlon1 and esπlon2 respectively. The area of each plate is equal to S. Find :
View SolutionThe gap between the plates of a parallel-plate capacitor is filled with istropic dielectrc whose permittlvity ε varies linearly from esπlon1 to ε2(ε2>ε1) in the direction perpendicular to the plates. The area of each plate equals S, the separation between the plates is equal to d. Find :
(a) the capacitance of the capacitor,
(b) the space density of the bound chagres as a function of a if the charge of the capacitor is q and E in it is directed toward the growing ε values.
View SolutionTwo spheres of radius R1 and R2 respectively are charged and joined by wire. The ratio of electric field of spheres is
View Solution
