There is a double-layer cylindrical capacitor whose parameters are shoen in Fig. The breakdown field strength values for these dielectrics are equal to E1 and E2 respectively. What is the breakdown voltage of this capacitor if ε1R1E1<ε2R2E2 ?

Let, λ be the inear charge density then, the sought potentail difference,
φ+−φ−=∫R2R1λ2πε0ε1rdr+∫R2R1λ2πε0ε2rdr
=λ2πε0[1ε1InR2/R1+1ε2InR3/R2]
Now, as, E1R1ε<E2R2ε2, so
λ2πε0=E1R1ε1
is the maximum aacceptable value, and for values greater than E1R1ε1, dielectric breakdowns will take place,
Hence, the maximum potential difference between teh plates,
φ+−φ−=E1R1ε1[1ε1InR2/R1+1ε2InR3/R2]=E1R1[InR2/R1+ε1ε2InR3/R2]
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
A double-layer cylindrical capacitor consists of conductors of radii R1 and R3 and two layers of dielectrics of relative permittivtties ε1 and esπon2. The radius of the common surface of the dielectrics. Is R2 . The breakdown field strengths of the dielectrics are E1 and E2 respectively. What is the breakdown voltage of this capacitor if (a) ε1R1E1<ε2R2E2 (b)ε2R2E2>ε1E1R1?
[Hint: If E1=E1max and E2>,E2max dielectric 1 will break first and if E2=E2max'E1>E1max dielectric 2 will break first.]View SolutionFind the dimension of 1(4π)ε0e2hc)
View Solution
Knowledge Check
- Question 1 - Select One
For the circuit shown in the figure the rms value of voltage across R and coil are E1 and E2 respectively.
The power (thermal) developed across the coil is
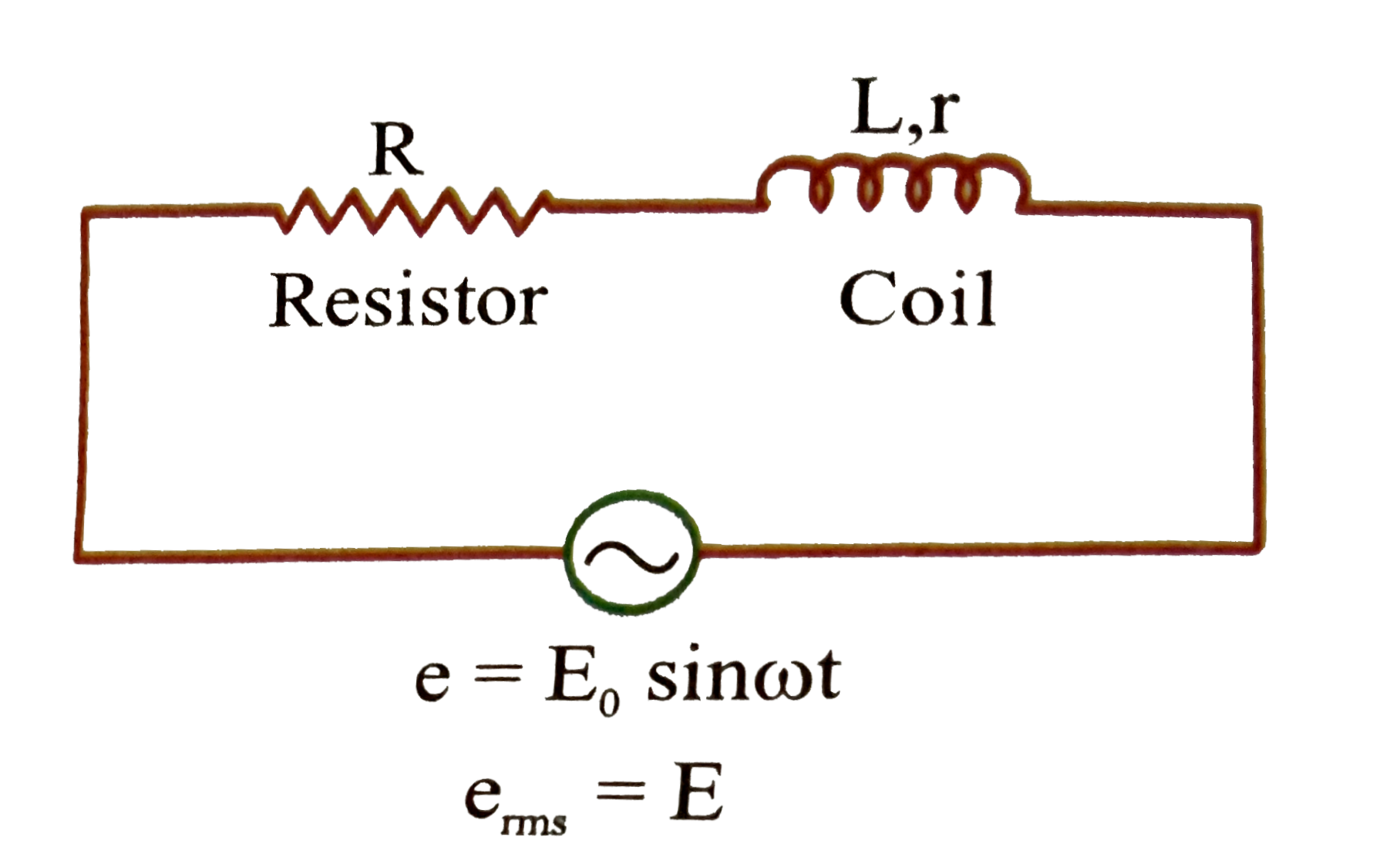 AE−E212RBE−E21−E222RCE22RD(E−E1)22R
AE−E212RBE−E21−E222RCE22RD(E−E1)22R - Question 2 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 ir r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r31r32 if r1<R and r2<RDE1E2=r21r22 ir r1<R and r2<R - Question 3 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 if r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r22r32 if r1<R and r2<RDE1E2=r21r22 if r1<R and r2<R
The dimensions of 1ε0e2hc are
View SolutionA cylindrical capacitor is filled with two cyclindrical layers of dielectric with permittivity esπlon1 and esπlon2. The inside radii of the layers are equal to R1 and R2>R1. The maximum permissible values of electric field strength reaching teh breakdown value for both dielectrics simulttaneously ?
View SolutionCharge is uniformly distributed with density ρ in a cylindrical region of radius R and infinite length. The magnitude of electric field at distance R2 and 2R from the axis of the cylinder is E1 and E2 respectively. The ratio E1E2 is equal to ___________.
View SolutionFor the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
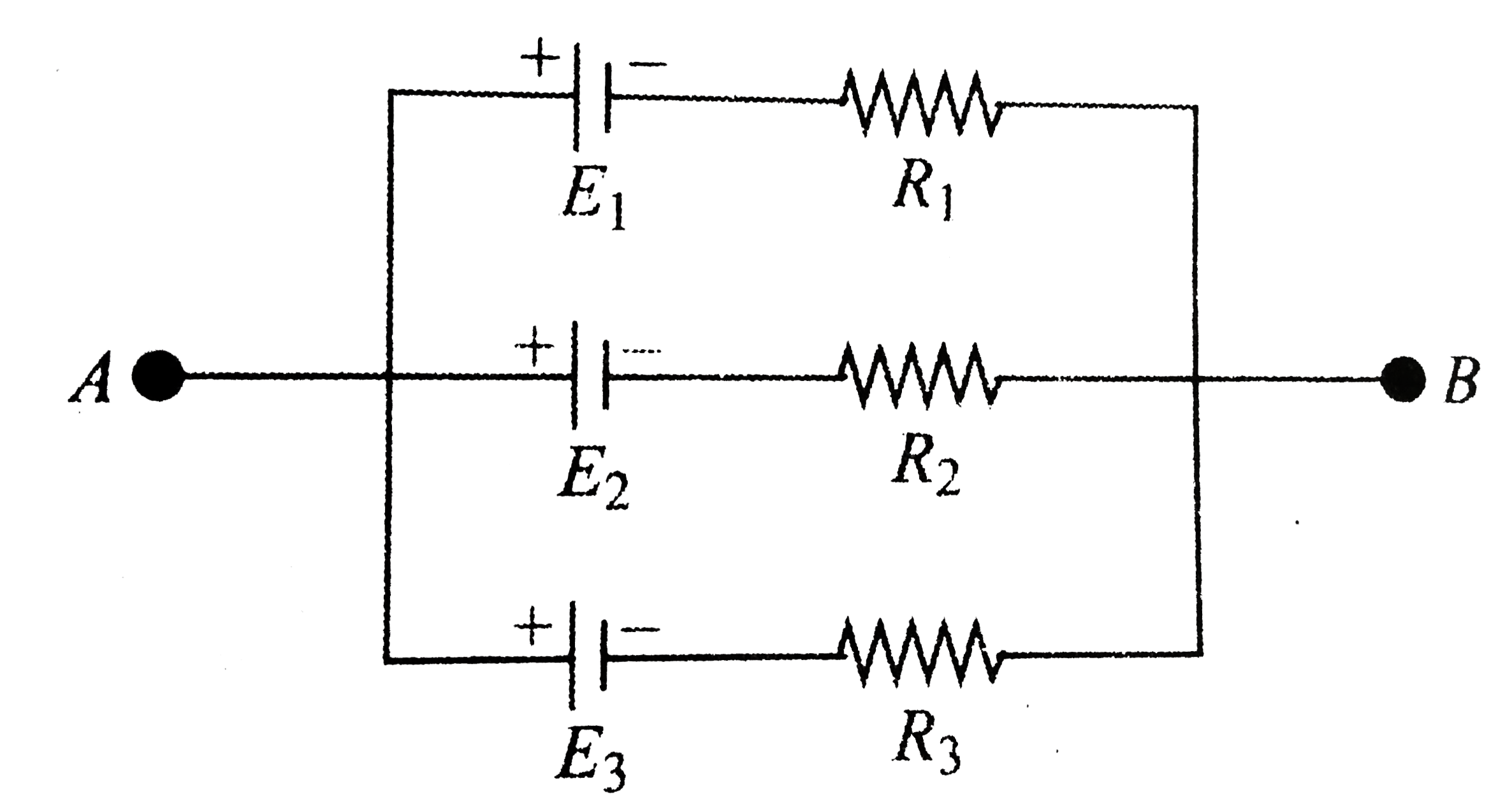 View Solution
View SolutionTwo batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
View Solution

