A conducting current-carrying plane is placed in an external unifrom magnetic field. As a result, the magnetic induction becomes equal to B1 on one of the plane and too B2 on the other. Find the magnetic force acting per unit area of teh plane in hte cases illiustrated in FIg. Determine the direction of the current in the plane in each case.
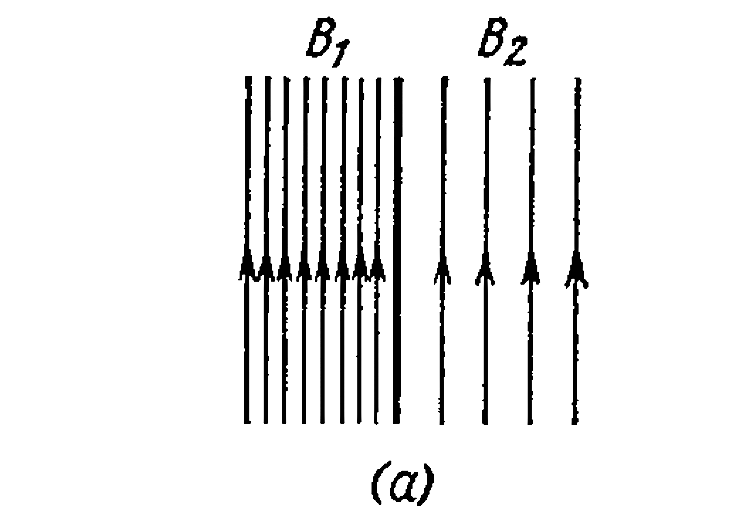


(a) The external field must be B1+B22 , which when superposed with the internal field B1−B22 (of opposite sign on the two sides of the plates) must give actual field. Now
B1−B22=12μ0i
or, i=B1−B2μ0
Thus, F=B21−B222μ0

(b) Here, the external field must be B1−B22 upward with an internal field, B1+B22, upward on the left and downward on the right. Thus,
i=B1+B2μ0 and F=B21−B222μ0

(c) Our boundary condition following from Gauss's law is B1cosθ1=B2cosθ2.
Also , (B1sinθ1+B2sinθ2)=μ0i where
i = current per unit length
The external fied parallel to the plate must be B1sinθ1−B2θ22
(The perpendicular component B1cosθ1, does not matter since the corresponding force is tangetial)
Thus, F=B21sin2θ1−B22sin2θ22μ0 per unit area
B21−B222μ0 per unit area.
The direction of the current in the plane conductor is perpendicular to the paper and beyond the drawing .

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A conducting current-carrying plane is placed in an external uniform magnetic field. As a result, the magnetic induction becomes equal to B1 on one side of the plane and equal to B2 on the other side. Find the magnetic force acting per unit area of the plane in the cases illustrated in the figure.
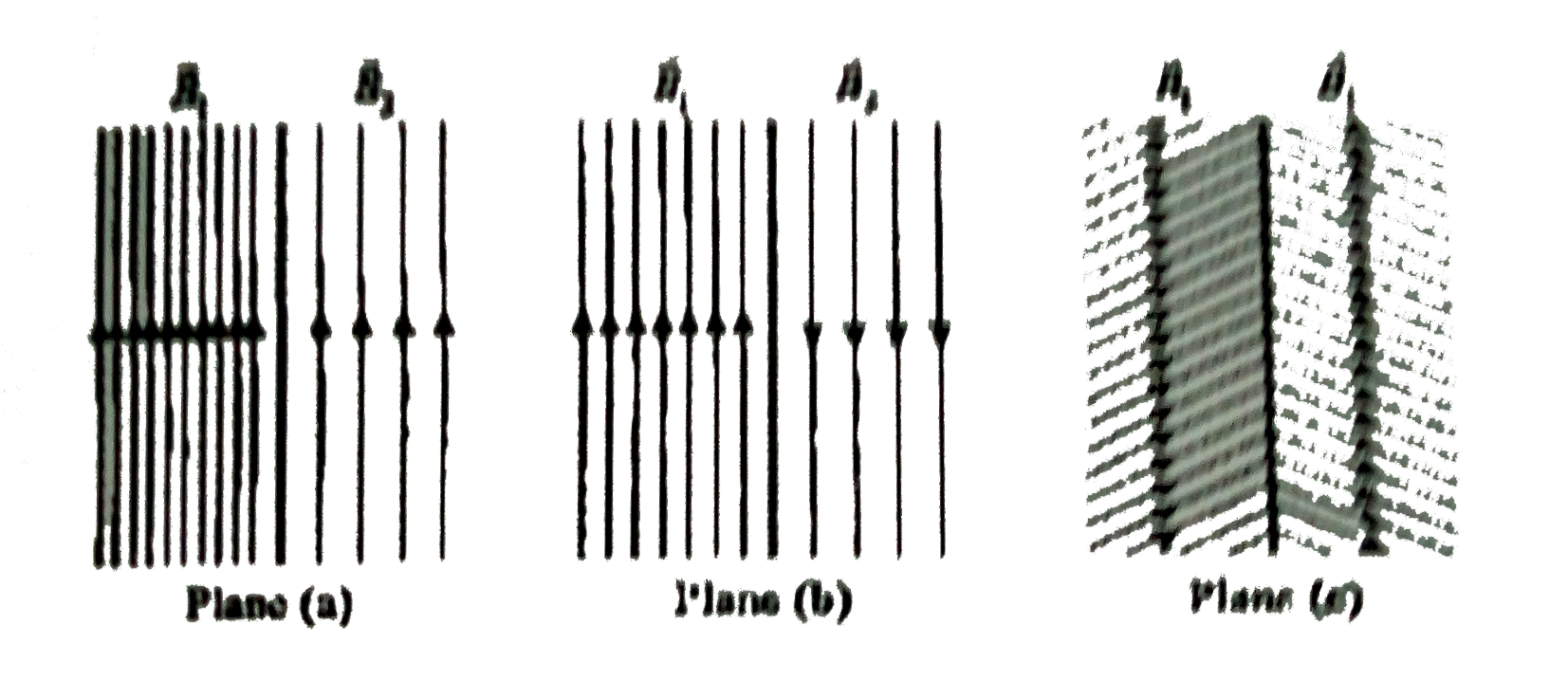
View SolutionA conducting current-carrying plane is placed in an external uniform magnetic field. As a result, the magnetic induction becomes equal to B1 on one side of the plane and B2 on the other side. Find the magnetic force acting per unit area of the plane.

View Solution
Knowledge Check
A current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic of paper. The magnetic force experienced by the loop is
 Anon-zeroBzeroCcannot say anythingDNone of these
Anon-zeroBzeroCcannot say anythingDNone of theseA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
 AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξs
AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξsA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
AI r BB2πrIBCzeroDπrIB
A conducting current-carrying plane is placed in an external uniform magnetic field. As a result, the magnetic induction becomes equal to B1 on one side of the plane and B2 on the other side. Find the magnetic force acting per unit area of the plane.

View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionA system consists of two parallel plane carrying currents producing a uniform magnetic field of induction B between the planes. Outside this space there is no magnetic field. The magnetic force acting per unit area of each plane is found to be B2/Nμ0. Find N.
View SolutionA system consists of two parallel plane carrying currents producing a uniform magnetic field of induction B between the planes. Outside this space there is no magnetic field. The magnetic force acting per unit area of each plane is found to be B2/Nμ0. Find N.
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View Solution
