A sytem consists of a long cylindrical anode of radius a and a coxial cylindrical cylindrical cathode of radius b(b<a). A filament located along the axis of the system carries a heating current I producing a magnetic field in the surrounding space. FInd the least potentilal differnce between the cathode and anode at which the therimal electrons leaving the cathode without intital velcity start reaching the anode.
When a current I flows along the axis, a magnetic field Bφ=μ0I2πp is set up where ρ2=x2+y2. In terms of components,
Bx=−μ0ly2πρ2,By=μ0lx2πρ2 and Bx=0
Suppose a p.d. V is set up between the inner cathode and the other anode. This mean a potential function of the form
φ=VInρ/bIna/b,a>ρ>b,
as one can check by solving Laplace equaction , The electric field corresponding to this is,
Ex=Vxρ2Ina/b,Ey=Vyρ2Ina/b,Ex=0.
The equactions of motion are,
ddtmvx=+|e|Vzρ2Ina/b+|e|μ0I2πρ2x.z
ddtmvy=+|e|Vzρ2Ina/b+|e|μ0I2πρ2y.z
and ddtmvx=−|e|μ0I2πρ2(x.x+y.y)=−|e|μ0I2πddtInρ
(−|e|) is the charge on the electron.
Intergrating the last equaction,
mve=−|e|mm0I2πInρ/a=m.z.

since vz=0 where ρ=a. We know substitude this .z in the other two equactions to get
ddt(12mv2x+12mv2y)
=[|e|vIna/b−|e|2m(μ0I2π)2Inρ/b].x.x+y.yρ2
=[|e|VInab−|e|2m(μ0I2π)2Inρb].12ρ52ddtρ2
=[|e|VInab−|e|2m(μ0I2π)2Inρb]ddtInρb
Intergating and using v2=0, at ρ=b, we get,
12mv2==[|e|VInabINρb−12m|e|2(μ0I2π)2(Inρb)]
The RHS must be positive, for all a>ρ>b. The condition for this is,
V≥12|e|m(μ0I2π)2Inab
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Magentron is a device consisting of a filament of radius a and coaxial cylindrical anode of radius b which are located in a unifrom magnetic field parallel to the filament. An accelerating potential differnece V is applied between the filament and the anode. Find the value of magnetic induction at which the electrons leaving the filamnent with zero velocity reach the anode.
View SolutionA wire of iength I carries a current along the x-axis. A magnetic field B=B0(ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View Solution
Knowledge Check
A long solenoid carrying a current produces a magnetic field B along its axis. If the number ofturns per cm is doubled and the current in the solenoid is halved, then the new value of the magnetic field along its axis will be
A2BBB2CBD4BA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the conductor is correctly represented by the figure:
A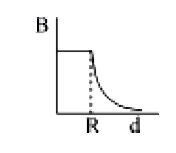 B
B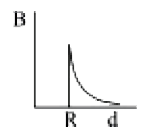 C
C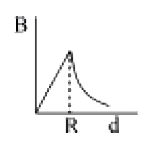 D
D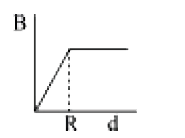
A cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
 A
A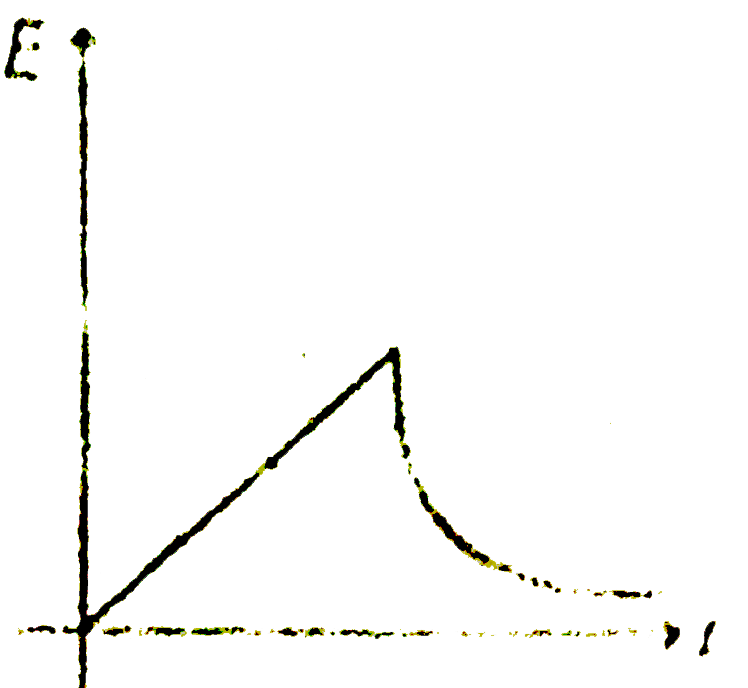 B
B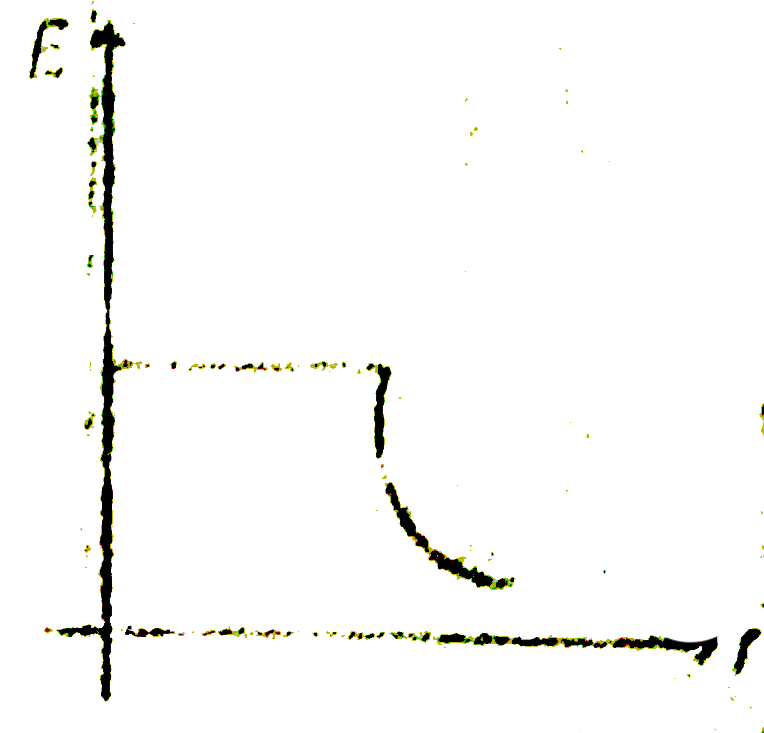 C
C D
D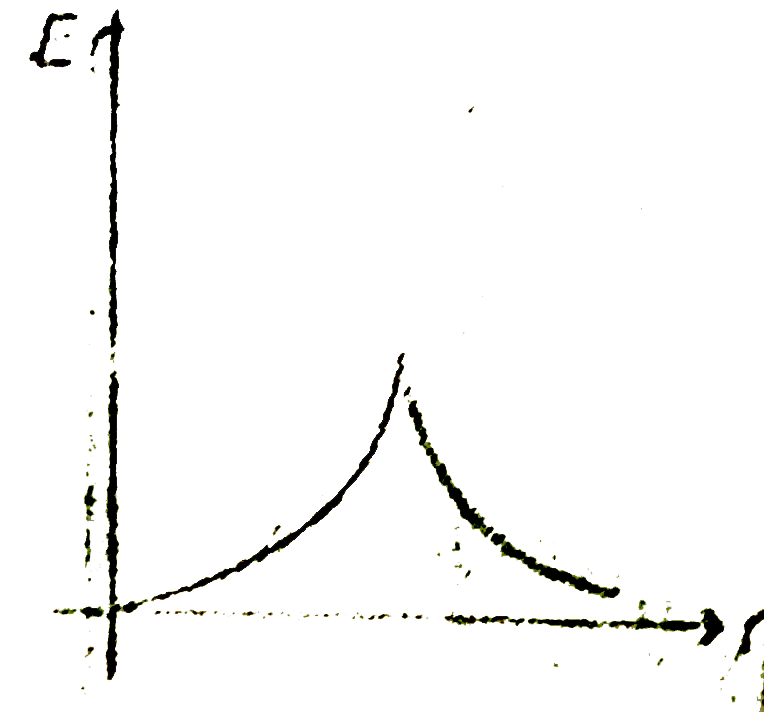
A wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA long straight metal rod has a very long hole of radius a drilled parallel to rod as shown in the figure. If the rod carries a current i. Find the magnetic field (a) on the axis of the rod. (b) on the axis of the hole.

View SolutionA 20 cm long cylindrical vessel has a radius of 8 cm. The total surface area (in sq cm) of the cylindrical vessel is
View SolutionA long cylindrical conductor of radius a contains a long cylindrical holr of radius l. The axes of the two cylinders are parallel and are at a distance d apart. A current I is uniformly distributed over the cross-section. Find the magnetic field at the centre of the hole.
[Hint: Apply the principle of superposition of magnetic field]
View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is

View Solution
