A certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
The equation of the circuit is
Ld2Qdt2+RdQdt+QC=0
where Q= charge on the capacitor,
This has the solution Q=Qme−βtsin(ωt+α)
whereβ=R2L,ω=√ω20−β2,ω20=1LC
NowI=dQDT=0 att=0
so , Qme−βt(−βsin(ωt+α)+ωcos(ωt+α))=0 at t=0
Thus ωcosα=βsinαor α=tan−1(ωβ)
Now Vm=QmC and V0=P.D.at =0=QmCsinα
∴V0Vm=sinα=ω√ω2+β2=ωω0=√1−β2/ω20=√1−R2C4L2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An oscillating circuit consists of a capacitor with capacitance C, a coil of inductance L with negligible resistance, and aswitch. With the switch disconnected , the capacitor was charged to a voltage Vm and then at the moment t=0 the switch was closed . Find :
(a) the current (I(t)) in the circuit as a function of time,
(b) the emf of self- inductance in the coil at the moments when the electric energy of the capacitor is equal to that of the current in the coil.
View SolutionFind how the voltage across the capacitor C varies with time t after closing of the switch Sw at the moment t=0.
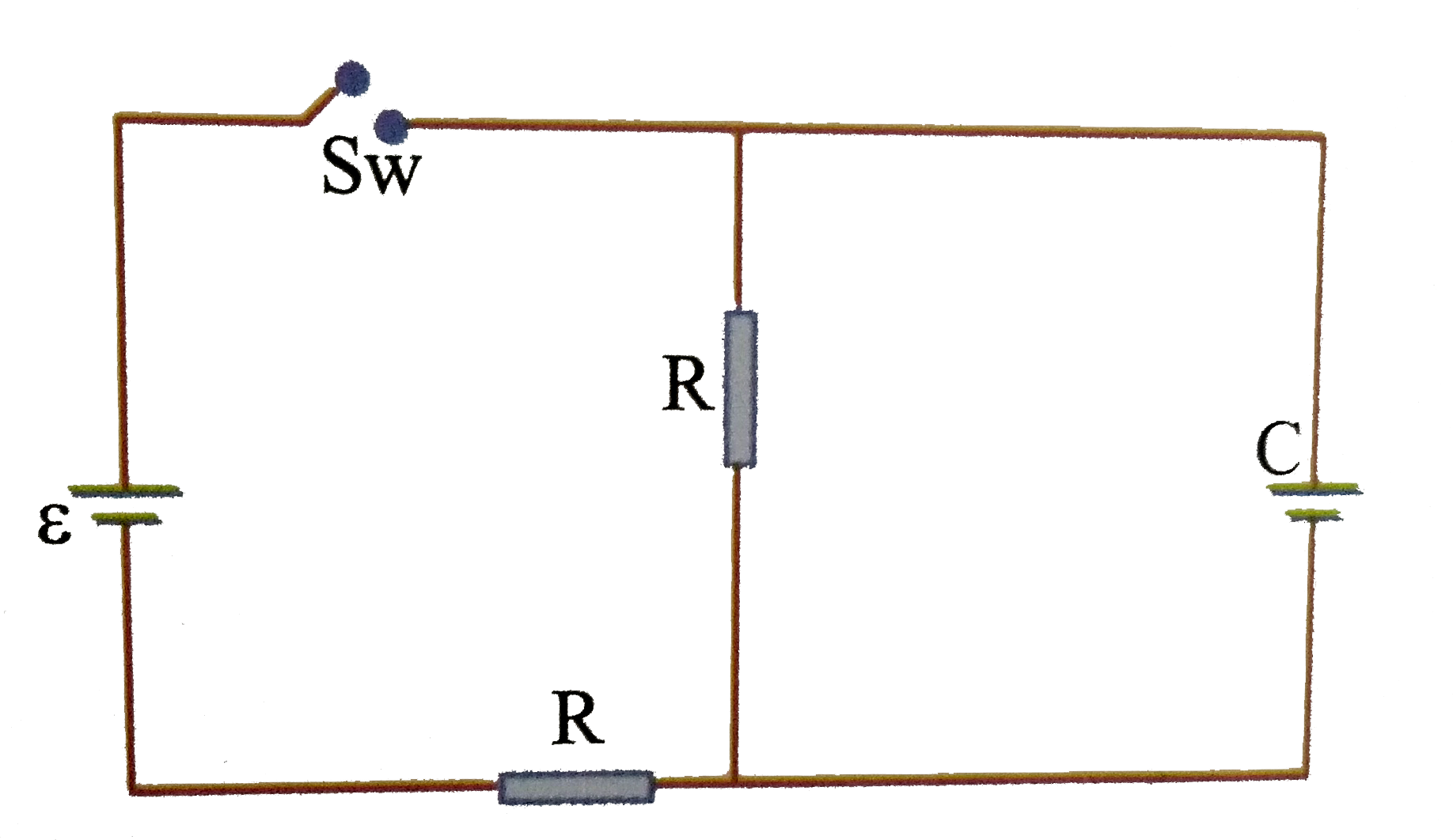 .
.
View Solution
Knowledge Check
In the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
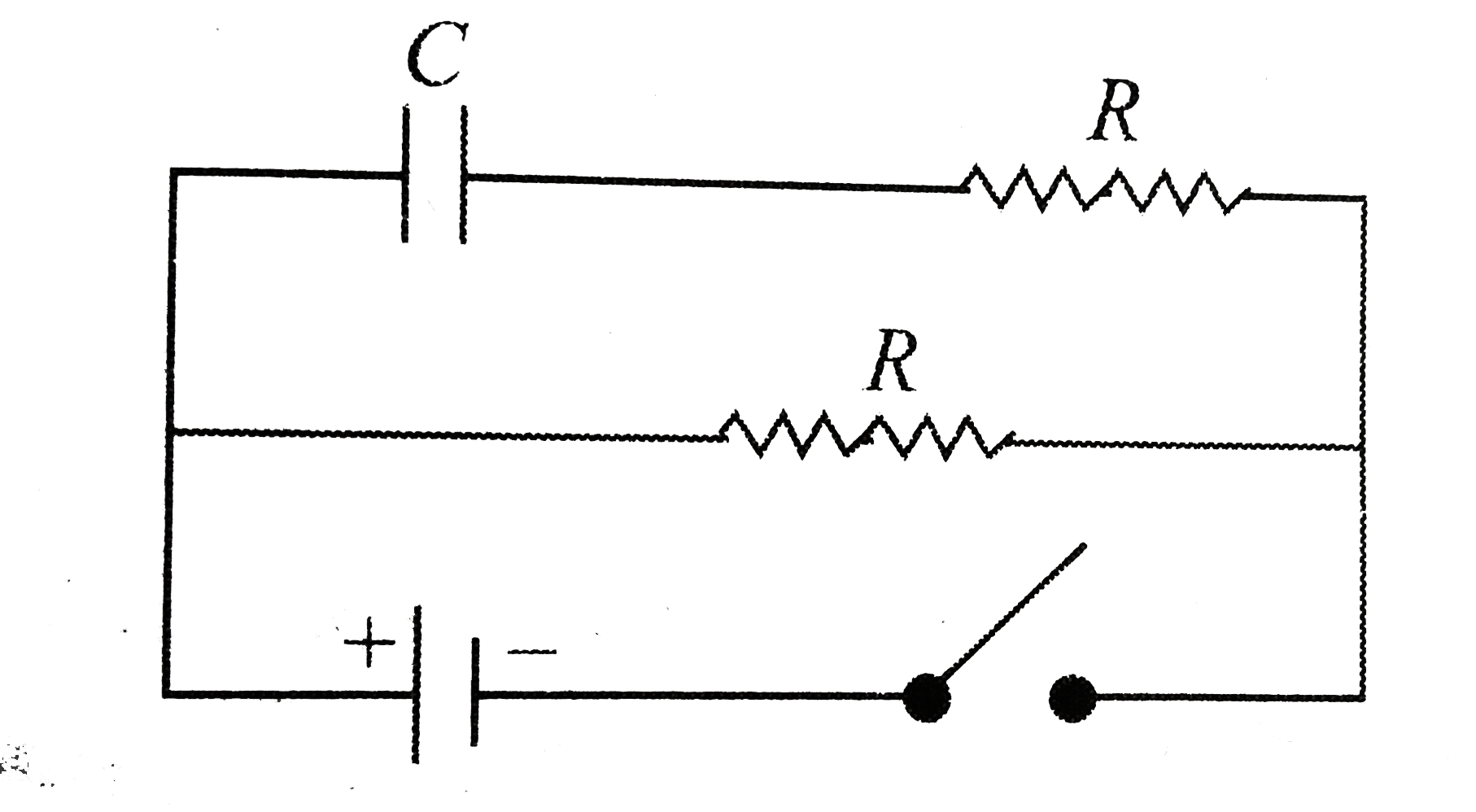 ARCB2 RCC12RCDRC log2
ARCB2 RCC12RCDRC log2In the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
 A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μC
A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μCIn the circuit shown, the capacitor is initially uncharged. The switch S is closed at t = 0. Time after which voltage across capacitor and resistor are equal is:
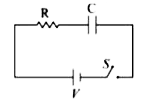 ARCln12BRCln2CRCln32DRC
ARCln12BRCln2CRCln32DRC
An oscillating circuit consist of a capacitor with capacitance C=4.0μF and a coil with inductance L=2.0μH and active resistance R=10Ω. Find the ration of the energy of the coil's magnetic field to that of the capacitor's electric field at the moment when the current has the maximum value .
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View SolutionFind the charge on each of the capacitor 0.20ms after the switch S is closed in Figure.
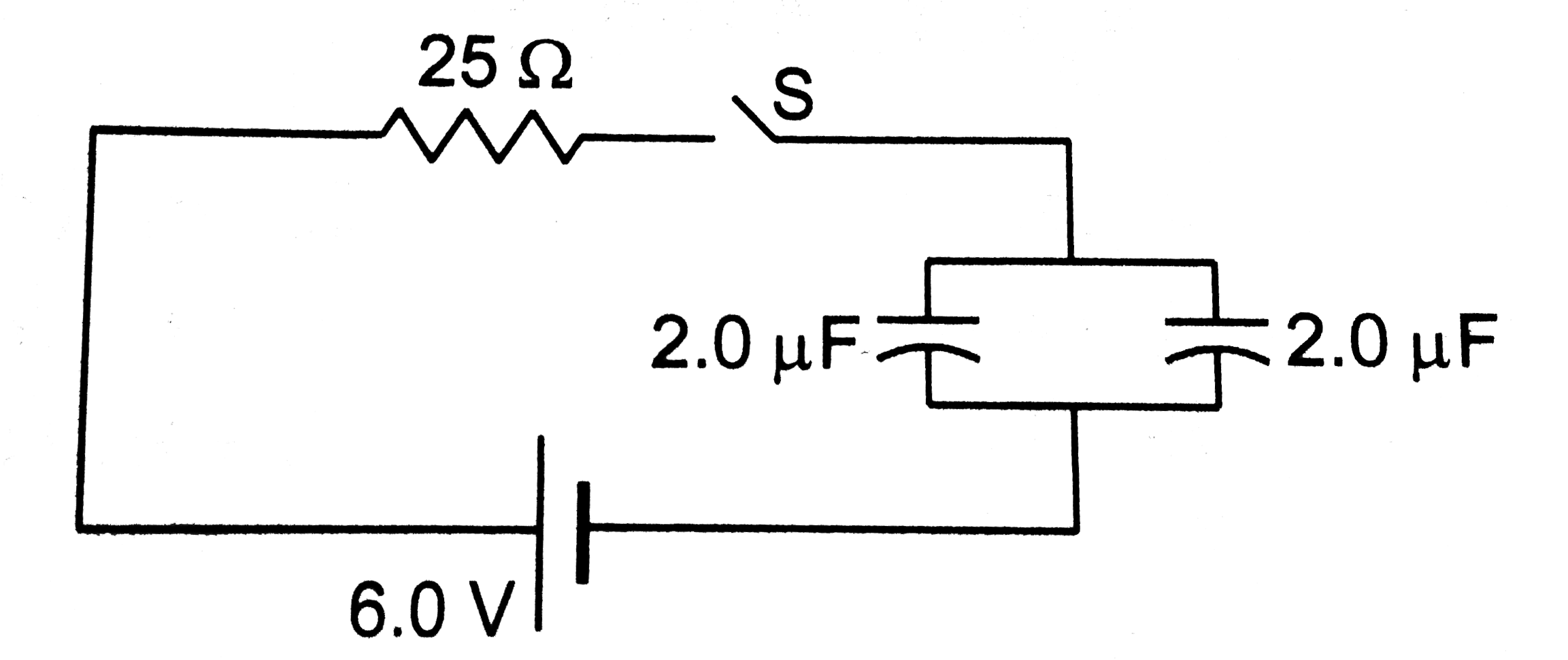
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionA series circuit consisting of a capacitor with capacitance with capacitance C, a rasistance R, and a coil with inductance L and negligible active resistance is connected to an oscillator whose frequency can be varied without changing the voltag amplitude. Find the frequency at which the voltage amplitude is maximum
(a) across the capacitor ,
(b) across the coil.
View Solution
