Find the damped oscillation frequency of the circuit shown in figure. The capacitance C, inductance L, and active resistance R are supposed to be known. Find how must C,L,andR be interrelated to make oscillations possible.
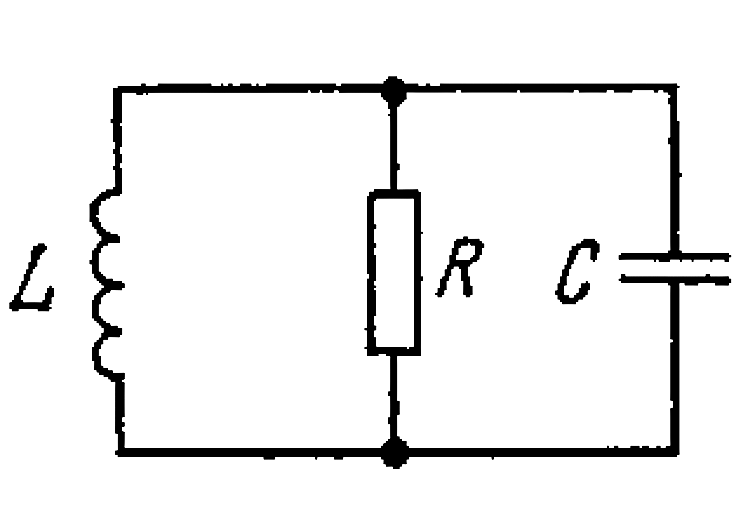
Given q=q1+q2
I1=−.q1,I2=−.q2
LI1=RI2=qC.
Thus CL..q1+(q1+q2)=0
RC.q2+q1+q2=0
Putting q1=Aeiωt q2=Be+iωt
(1−ωLC)A+B=0
A+(1+iωRC)B=0
A solutiion exists only if
(1−ω2LC)(1+iωRC)=1
or iωRC−ω2LC−iω3LRC2=0
or LRC2ω2−iωLC−RC=0
ω2−iω1RC−1LC=0
ω=i2RC±√1LC−14R2C2≅iβ±ω0
Thus q1=(A1cosω0t+A2sinω0t)e−βtetc
ω0 is the oscillation frequency. Oscillations are possible only if ω20>0
i.e. 14R2<CL

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
In the L-C-R circuit as shown in figure,
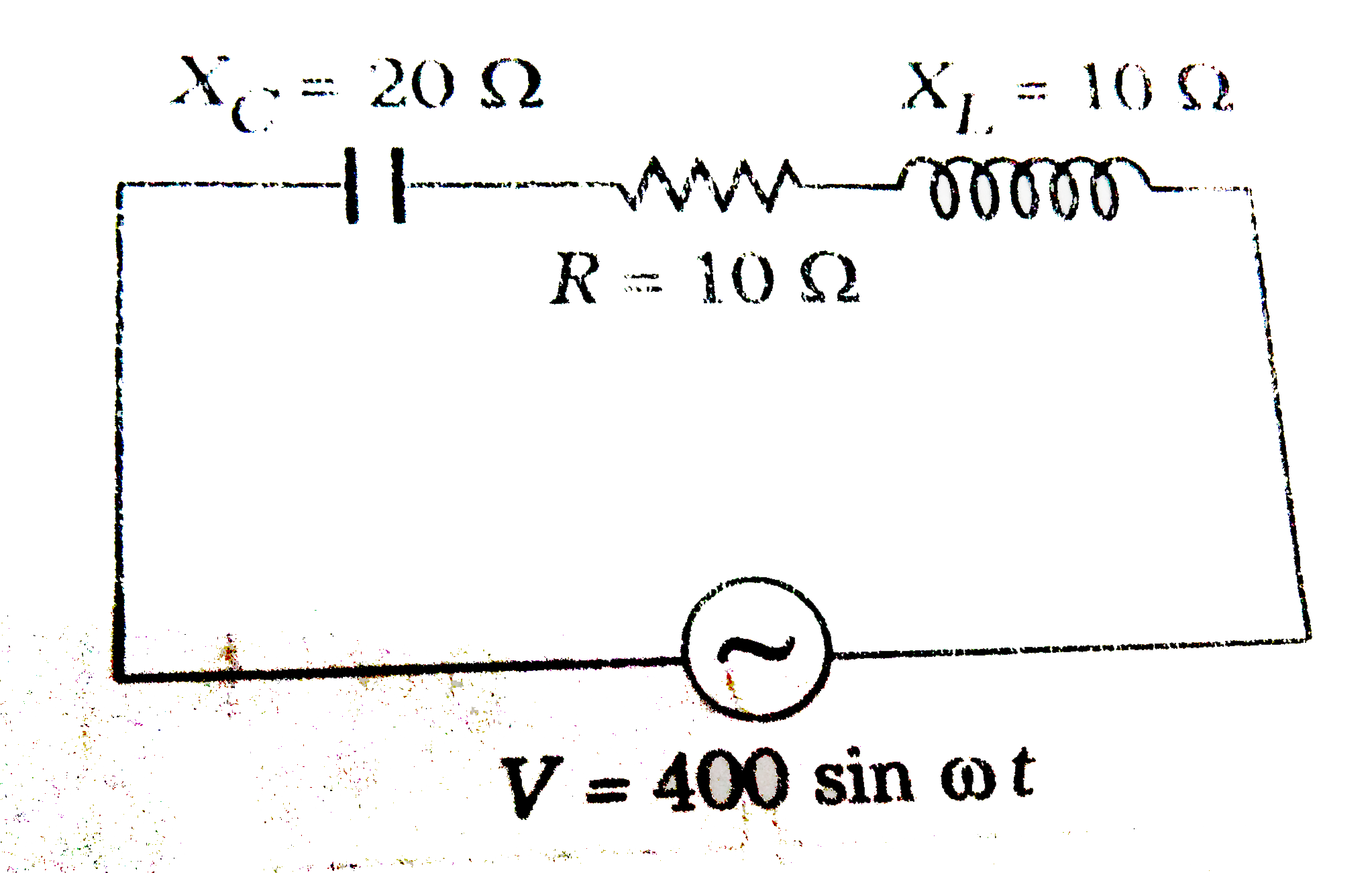 ACurrent will lead the voltageBRuns value of current is 20 ACPower factor of the circuit is 1√2DVoltage drop across resistance is 200 V
ACurrent will lead the voltageBRuns value of current is 20 ACPower factor of the circuit is 1√2DVoltage drop across resistance is 200 VAn LC series circuit with an inductance L and a capacitance C has an oscillation frequency f. Two isolated induc tors, each with inductance L, and two capacitors, each with capacitance C, are all wired in series and the circuit is com pleted. The oscillation frequency is
Af4Bf2CfD4 f
There are two oscillating circuits (figure) with capacitors of equal capacitances. How must inductances and active resistances of the coils be interrelated for the frequencies and damping of free oscillations in both circuits to be equal ? The mutual inductance of coils in the left circuit is negligible.

View SolutionA certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View SolutionIn the circuit shown, find the value of resistance R in terms of inductance L and capacitance C such that the current through the cell remains constant forever after the switch is closed.
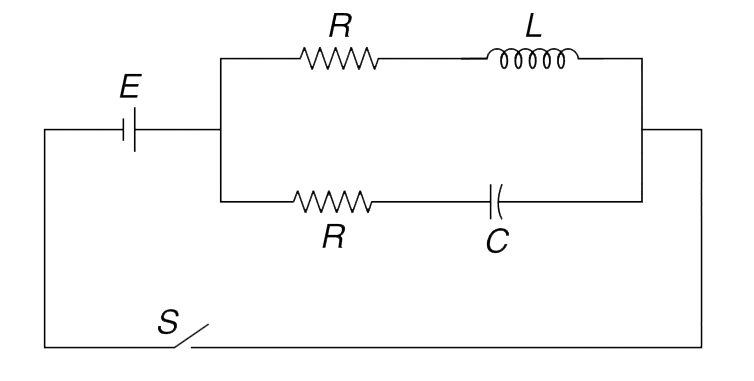
View SolutionAn LC series circuit has an oscillation frequency f. Two isolated inductors, each with inductance L and two capacitors each with capacitance C, all are connected in series and circuit is completed. The oscillation frequency is
View SolutionAn oscillating circuit consist of a capacitor with capacitance C=4.0μF and a coil with inductance L=2.0μH and active resistance R=10Ω. Find the ration of the energy of the coil's magnetic field to that of the capacitor's electric field at the moment when the current has the maximum value .
View Solution
