A parellel-plate capacity whose electrodes are shaped as round disc is changed slowly. Demonstrate that the flux of the Poynting vector across the capacitor's lateral surface is equal to the increment of the capcitor's enegry per unit time. The dissipation of field at the edge is to be neglected in calculations.
If the charge on the capacitor is Q, the rate of increase of the capcitor's energy
=ddt(12Q2c)=QQC=dε0πR2QQ
Now electric field betweeb the pates (inside it) is, E=QπR2ε0.
So discplacement current =∂D∂t=QπR2
This will lead to a magnetic field, (circuital) inside the plates . At a radial distance r
2πrHθ(r)=πr2QπR2 or Hθ=Qr2πR2
Hence Hθ(R)=Q2πR at the edge.
Thus inward polynting vector =S=Q2πR×QπR2ε0
Total flow =2πRd×S=QQdπR2ε0 Proved
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
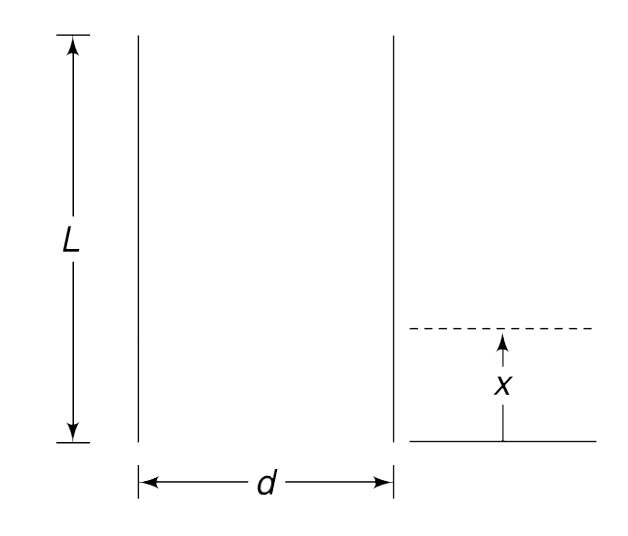
A parallel plate capacitor has square plates of side length L. Plates are kept vertical at separation d between them. The space between the plates is filled with a dielectric whose dielectric constant (K) changes with height (x) from the lower edge of the plates as K=eβx where b is a positive constant. A potential difference of V is applied across the capacitor plates.
(i) Plot the variation of surface charge density (s) on the positive plate of the capacitor versus x.
(ii) Plot the variation of electric field between the plates as a function of x.
(iii) Calculate the capacitance of the capacitor.
View SolutionA current flowing in the winding of a long straight solenoid is increased at a sufficiently slow rate. Demonstrate that the rate at which the enrgy of the magnetic field in the solenoid increases is equal to the flux of the Poynting vector across the lateral surface of the solenoid.
View SolutionThe space between the electrodes of a parallel-plate capacitor is filled with a uniform poorly conducting medium of conductivity σ and permittivity ε. The capacitor plates shaped as round discs are separted by a distance d. Neglecting the edge effects, find the magnetic field strength between the plates at a distance r from their axis if an ac voltage V=Vmcosωt is applied to the capacitor.
View Solution
