Proceeding from Fermat'sprinciple derive the refraction formula for paraxial rays on a spherical boundary surface of radius R between media with refractive indices n and n'.
For O1 to be image, the optical paths of all rays OAO1 must be equal upto terms of leading order in h. Thus
n1OA+n2AO1= constant
But, OP=|s|,O1P=|s| and so
OA=√h2+(|s|+∂)2≅|s|+∂+h22|s|
O1A=√h2+(|s'|−∂)2≅|s'|−∂+h22|s'|
(neglecting products h2∂). Then
n1|s|+n2|s'|+n1∂−n2∂+h22(n1|s|+n2|s'|)= const.
Now (r−∂)2+h2=r2
or h2=2r∂ or ∂=h22r
Here r=CP.
Hence n1|s|+n2|s'|+h22{n1−n2r+n1|s|+n2s'∣}= constant
Since this must hold for all h, we have
n2|s'|+n1|s|=n2−n1r
From our sign convention, s'>0,s<0 so we get
n2s'−n1s=n2−n1r.

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Using Fermat's principle derive the laws of deflection and refraction of light on the plane interface between two media.
View Solution(a) A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices nx and n2(n2>n1)
Draw the ray diagram and deduce the relation between the object distance (w), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
(b) A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
View Solution
Knowledge Check
A transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
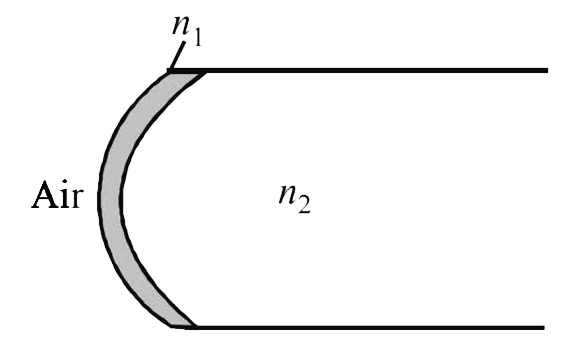 A|f1|=3RB|f1|=2.8RC|f2|=1.4RD|f2|=5.4R
A|f1|=3RB|f1|=2.8RC|f2|=1.4RD|f2|=5.4RA biconvex lens made of material with refractive index n2. The radii of curvatures of its left surface and right surface are R1 and R2. The media on its left and right have refreactive indices n1 and n3 respectively. The first and second focal lengths of the lens are respectively f1 and f2.
Assume that R1=R2,n1≠n3. The ratio, f1/f2, of the two focal lengths is equal toA1Bn1/n3Cn3/n1D(n3−1)/(n1−1)A transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1andn2(>n1), as shown in the figure. A ray of light is incident with angle θi, from medium 1 and emerges in medium 2 with refraction and θf, with a lateral displacement l.
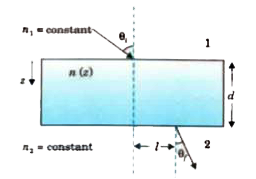
Which of the following statement(s) is (are) true ?Al is independent of n2Bn1sinθ1=n2sinθfCl is independent of n(z)Dn1sinθ1=(n2−n1)sinθf
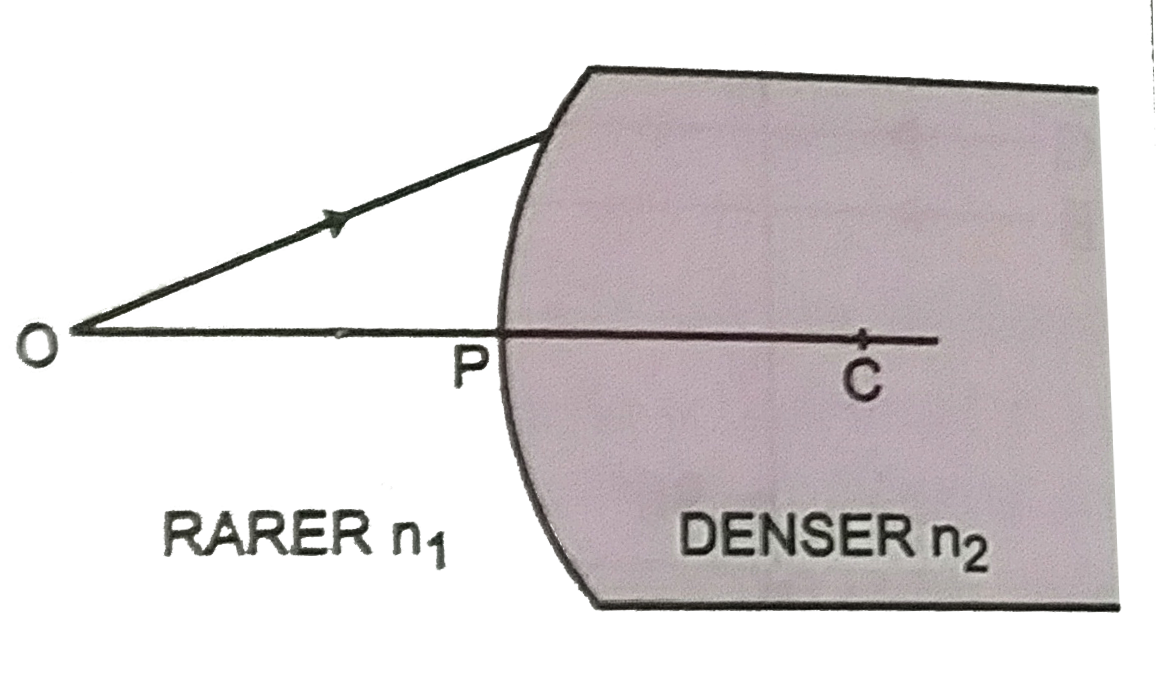
A spherical of radius of curvature R, separates a rarer and a denser medium as shown in Fig. Complete the path of the incident ray of light, showing the formation of a real image. Hence derive the relation connecting object distance u, image distance v, radius of curvature R and the refractive indices n1andn2 of the two media. Briefly explain how the focal length of a convex lens changes with increase in wavelength of incident light.
 .
.
View SolutionA point object 'O' on the principal axis of a spherical surface of radius of curvature 'R' separating two media of refractive indices n1andn2 forms an image 'I' as shown in the figure below. Prove that n2v−n1v=n2−n1R

View Solution(i) Device the mathematical n between refractive indices n1 and n2 of two radii and radius of curvature R for refraction at a convex shperical surface. Consider the object to be a point since lying on the principal axis in rarer medium of refractive index n1 and a real image formed in the denser medium of refractive index n2. Hence, derive lens marker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20cm. The distance of light source from the glass surface is 100cm. At what position is the image formed ?
View SolutionDerive the mathematical relation between refractive indices n1 and n2 of two media and radius of curvature R for refraction at a convex spherical surface. Consider the object to be a point one lying on the principal axis in rarer medium of refractive index nt and a real image formed in the denser medium of refractive index n2. Hence, derive lens maker's formula.
(ii) Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed ?
View SolutionDraw a ray diagram to show the formation of the real image of a point object due to a convex spherical refracting surface, when the ray of light is travelling from a rarer medium of refractive index nx to a denser medium of refractive index n2 .
Using this diagram derive the relation between object distance (w), image distance (v), radius of curvature (R) of a convex spherical surface. State the sign convention and the assumptions used.
View Solution
