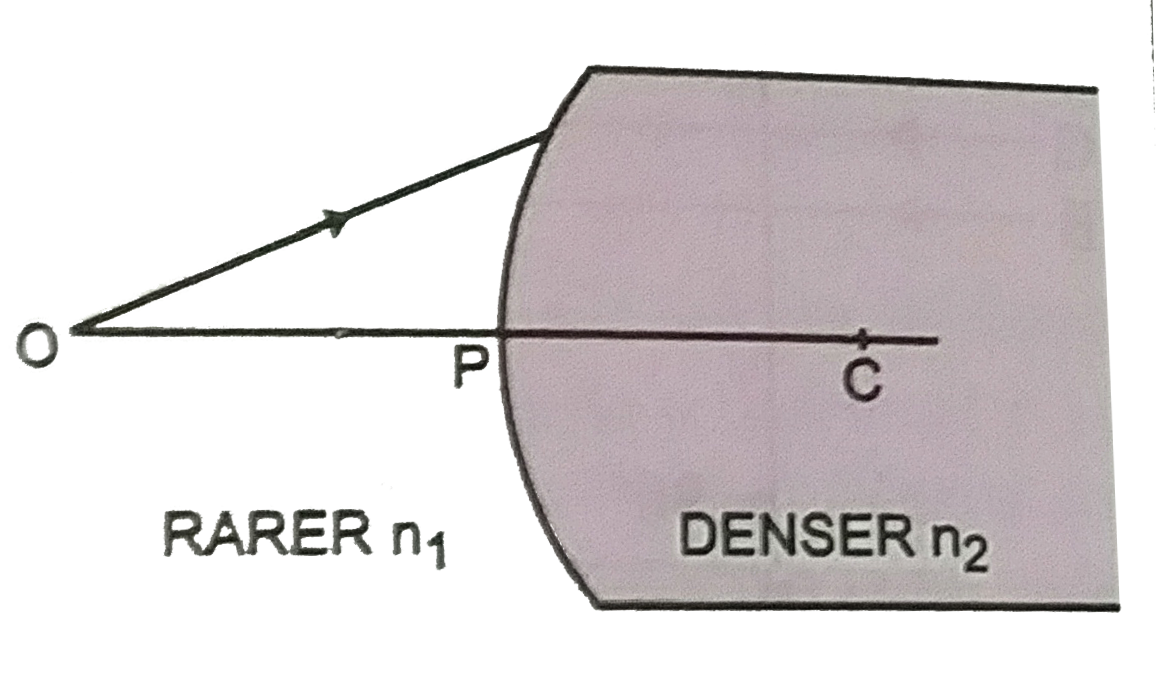
A spherical of radius of curvature R, separates a rarer and a denser medium as shown in Fig. Complete the path of the incident ray of light, showing the formation of a real image. Hence derive the relation connecting object distance u, image distance v, radius of curvature R and the refractive indices n1andn2 of the two media. Briefly explain how the focal length of a convex lens changes with increase in wavelength of incident light.
 .
.
Step by step video & image solution for A spherical of radius of curvature R, separates a rarer and a denser medium as shown in Fig. Complete the path of the incident ray of light, showing the formation of a real image. Hence derive the relation connecting object distance u, image distance v, radius of curvature R and the refractive indices n_1 and n_2 of the two media. Briefly explain how the focal length of a convex lens changes with increase in wavelength of incident light. . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (c)
8 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (d)
6 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (NCERT)Short Answer
6 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
(a) A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices nx and n2(n2>n1)
Draw the ray diagram and deduce the relation between the object distance (w), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
(b) A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
View SolutionDraw a ray diagram to show the formation of the image of an object placed between the optical centre and focus of a convex lens. Deduce the relationship between object distance, image disatnce and focal length of lens.
View Solution
Knowledge Check
The two spherical surfaces of a double concave lens have the same radius of curvature R, and the refractive index of the medium enclosed by the refracting surfaces is μ then the focal length of the lens is
Af=R2Bf=R2(μ−1)Cf=R2(1−μ)Df=−(μ−1)R2A plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
A50 cmB100 cmC200 cmD150 cmIf the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
Af=R2(μ+1)Bf=2R(μ+1)Cf=2Rμ+1Df=R2(μ−1)
Proceeding from Fermat'sprinciple derive the refraction formula for paraxial rays on a spherical boundary surface of radius R between media with refractive indices n and n'.
View SolutionDraw a ray diagram to show the formation of the image of an object placed between the optical centre and principal focus of a convex lens. Deduce the relationship between the object distance, image distance and focal length under the conditions stated.
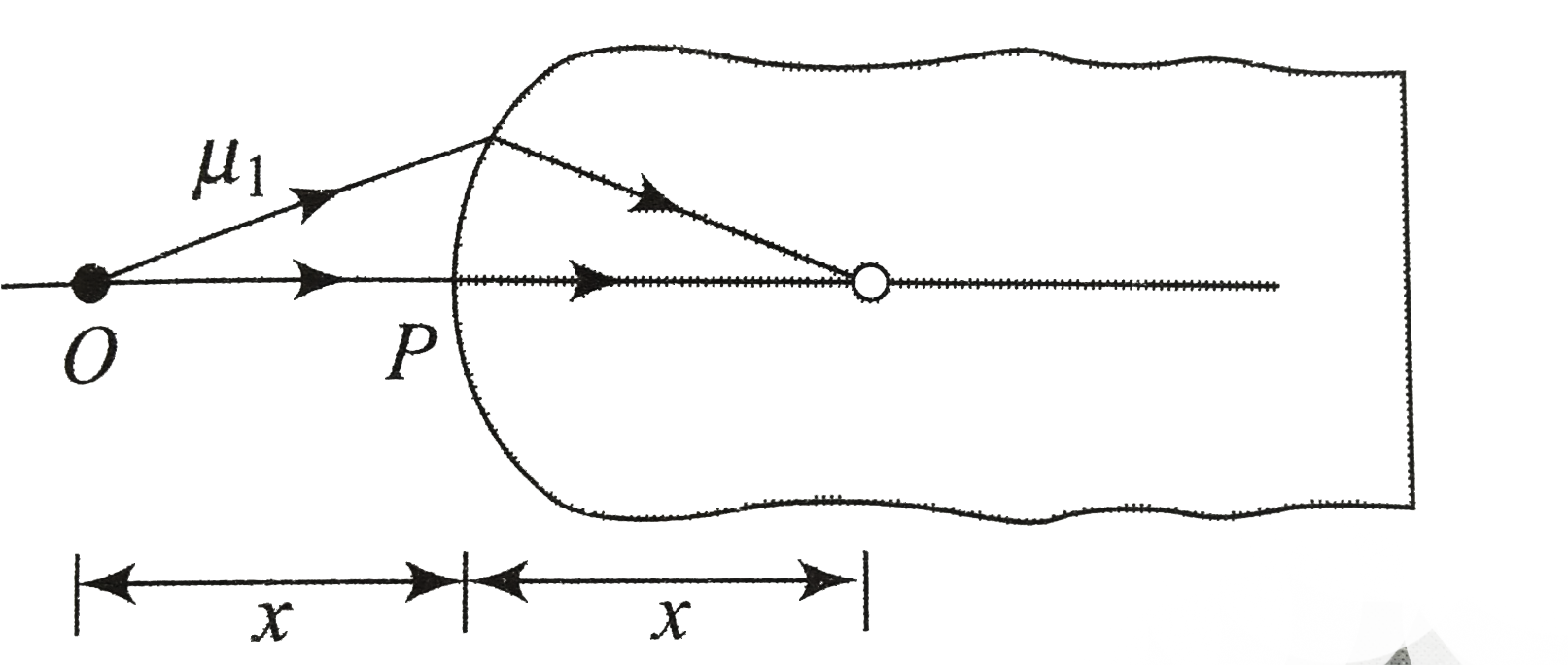
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionIf x , y and z denote the object distance, image distance and the radius of curvature respectively of a spherical mirror, which one of the following is the correct relation between them ?
View SolutionWhat acn be the largest distance of an image of a real object from a convex mirror of radius of curvature 20 cm
View Solution