A beam of X-rays with wavelength λ falls at a glancing angle 60.0∘ on a linear chain of scattering centres with period a. Find the angles of incidence corresponding to all diffraction maxima if λ=2a/5.
Path difference
=BC−AD
=a(cos60∘−cosα)
For diffraction maxima
a(cos60∘−cosα)=kλ,
since λ=25a, we get
cosα=12−25k
and we get K=−1,cosα=12+25=0.9,α=26∘
K=0,cosα=12=0.5,α=60∘
k=1,cosα=12−25=0.1,α=84∘
k=2,cosα=12−45=−0.3,α=107.5∘
k=3,cosα=12−65=−0.7,α=134.4∘
other values of k are not allowed as they lead to |cosα|>1.

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light43videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light24videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
A parallel beam of X-rays with a wavelenght of 1.47 Å falls at a glancing angle of 31∘3' on a face of a rocksalt crystal. Find the spacing between the atomic planes of the crystal, if the second - order diffraction maximum is observed at this angle.
View SolutionA beam of X-rays with wavelength λ=40± falls normally on aplne rectangular array of scattering centres and produces a system of diffraction maxima (Fig.) on a plane screen removed from the array by a distance l=10cm. Find the array periods a and b along the x and y axes if the distance between symmetrically located maxima of second order are equal to Δx=60mm (along the x axis) and Δy=40mm (along the yaxis).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
AλdBdλC2λdD2dλ - Question 2 - Select One
A ray of light of wavelength λ is incident on mirror at an angle of incidence 60∘. The wavelength of light after reflection will be
A2λB3λCλ/2Dλ
Light with wavelength λ=589.0nm falls normally on a diffraction grating with period d=2.5μm, comprising N=10000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionLight with wavelength λ falls on a diffracting grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle θ.
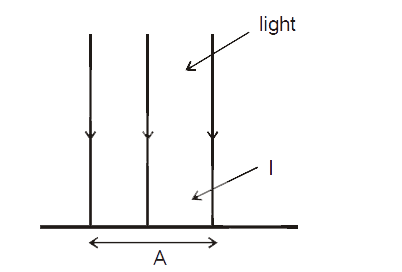
View SolutionA beam of light having wavelength λ and intensity 1 falls normally on an area A of a clean surface then
find out the number of photon incident on the surface.
 View Solution
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionA beam of X−rays with wavelength λ=174± falls on the surface of a single crystal rotating about its axis which is parallel let to its surface and perpendicular to the direction of the incident beam. In this case the direction to the maxima of second and third order from the system of planes parallel to the surface of the single crystal from an angle α=60∘ between them. Find the corresponding interplanar disatnce.
View SolutionA narrow beam of X-rays falls at a glancing angle of 20∘ on a diffraction grating with a constant of 2.0 μ m. The first diffraction maximum is observed at an angle of 12' to the direction of the beam. Find the wavelenght of the X-rays
View Solution

