How wide is the base of a trihedral prism which has the same resolving power as a diffraaction grating with 10000 lines in the second order of the spectrum if |dn/dλ|=0.10μm−1?
∣∣∣dndλ∣∣∣=kN=2×10,000
b×0.10μm−1=2×104
b=2×105μm=0.2m=20cm.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light43videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light24videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
Find the minimum magnitude of the magnetic field induction B at which a spectral instrument with resolving power λ/δλ==1.0.105 is capable of resolving the components of the spectral line λ=536nm caused by a transition between singlet terms. The observation line is at right angles to the magnetic field direction.
View SolutionA diffracting grating 1 cm wide has 1200 lines and is used in second order. What is the diffraction angle for light of wavelength 550 nm?
View SolutionThe ultimate resolving power λ/δλ of the spectrograph's trihedral prism is determined by diffraction of light at the prism edges (as in the case of a slit). When the prism is oriented to the least deviation angle in accordance with Rayleigh's criterion,
λ/δλ=b|dn/dλ|,
where b is the width of the prism's base (Fig.) and dn/dλ is the dispersion of its material. Derive this formula.
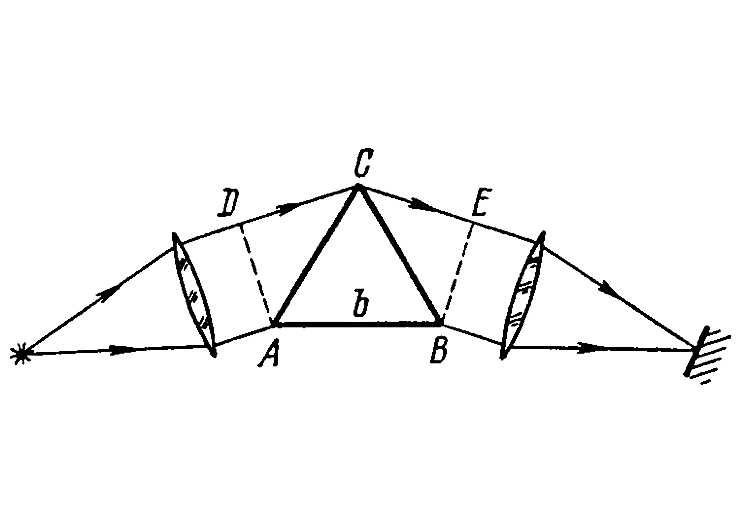 View Solution
View SolutionLight falls normally on a transparent diffraction grating of width l=6.5cm with 200 lines per millimetre. The spectrum under inverstigation includes a spectral line with λ=670.8nm consisting of two components differing by δλ=0.015nm. Find:
(a) in what order of the spectrum these components will be resolved,
(b) the least difference of wavelength that can be resolved by this grating in a wavelength region λ≈670nm.View SolutionFig. shows the plot of the function y(x) representing a fraction of the total power of thermal radiation falling within the spectral interval from 0 to x. Here x=λ/λm(λm is the wavelength corresponding to the maximum of spectral radiation density).
Using this plot, find:
(a) the wavelength which divides the radiation spectrum into two equal (in terms of energy) parts at the temperature 3700K,
(b) the fraction of the total radiation power falling within the visible range of the spectrum (0.40−0.76μm) at the temperature 5000K,
(c) how manu times the power radiated at wavelengths exceeding 0.76μm will increase if the temperature rises form 3000 to 5000K.
 View Solution
View SolutionWith light falling normally on a transparent diffraction grating 10mm wide, it was found that the components of the yellow line of sodium (589.0 and 589.6nm) are resolved beginning with the fifth order of the spectrum. Evaluate:
(a) the period of this grating,
(b) what must be the width of the grating with the same period for a double λ=460.0nm whose components differ by 0.13nm to be resolved in the third order of the spectrum.View SolutionLight with wavelength λ=589.0nm falls normally on a diffraction grating with period d=2.5μm, comprising N=10000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionWhat should be the length of a diffraction grating with a density of ruling of 300 slits per 1 mm to resolve two spectral lines of 6000.00 Å and 6000.50 Å wavelenght in the second-order spectrum ? What should be the length in the spectrum of the highest order?
View SolutionA plane light wave with wavelength λ=0.50μm falls normally on the face of a glass wedge with an angle Θ=30∘. On the opposite face of the wedge a transparent diffraction grating with period, d=2.00μm is inscibed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light froms with the directions to the principle Fraunhofer maxima of the zero and the first order. waht is the highest order of the spectrum? At what angle to the direction of incident light of the observed?
View SolutionFor the Fabry-Perot etalon of thickness d=2.5cm find:
(a) the highest order of interference of light with wavelength λ=0.50μm,
(b) the dispersion region Δλ, i.e the spectral interval of wavelengths, within which there is still no overlap with orders of interference if the observation is carried out appoximately at wavelength λ=0.50μm.View Solution

